Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(E,F\) lần lượt là trung điểm của \(B'C'\) và \(C'D'\). Mặt phẳng \(\left( {AEF} \right)\) chia hình hộp thành hai hình đa diện \(\left( H \right)\) và \(\left( {H'} \right)\) trong đó \(\left( H \right)\) là hình đa diện chứa đỉnh \(A'\). Tính tỉ số thể tích đa diện \(\left( H \right)\) và thể tích hình đa diện \(\left( {H'} \right)\).
-
A.
\(\dfrac{{25}}{{47}}\)
-
B.
\(\dfrac{{25}}{{72}}\)
-
C.
\(\dfrac{{47}}{{25}}\)
-
D.
\(\dfrac{{72}}{{47}}\)
+) Xác định thiết diện của hình hộp khi cắt với \(\left( {AEF} \right)\).
+) Tính thể tích của \(H'\) so với thể tích hình hộp, đưa về các bài toán tính thể tích khối chóp và cộng trừ thể tích.
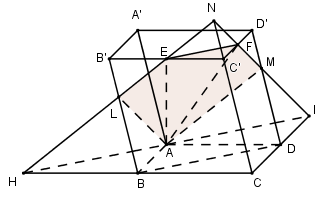
Mặt phẳng \(\left( {AEF} \right)\) chứa \(EF//BD \subset \left( {ABCD} \right)\)
\( \Rightarrow \) Giao tuyến của \(\left( {AEF} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng đi qua \(A\) và song song với \(EF\)
Trong \(\left( {ABCD} \right)\) qua \(A\) kẻ \(HI//BD\,\,\left( {H \in BC,I \in CD} \right)\)
Trong \(\left( {BCC'B'} \right)\) gọi \(L = EH \cap BB'\), trong \(\left( {CDD'C'} \right)\) gọi \(M = FI \cap DD'\), khi đó \(\left( {AEF} \right) \equiv \left( {ALEFM} \right)\)
Ta có : \(\left\{ \begin{array}{l}\left( {AEF} \right) \cap \left( {BCC'B'} \right) = HE\\\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI\\\left( {BCC'B'} \right) \cap \left( {CDD'C'} \right) = CC'\end{array} \right. \)
\(\Rightarrow HE,FI,CC'\) đồng quy tại \(N\).
Ta có : \({V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}}\)
Ta dễ dàng chứng minh được \(B,D\) lần lượt là trung điểm của \(CH,CI \Rightarrow BD = \dfrac{1}{2}HI \Rightarrow EF = \dfrac{1}{2}BD = \dfrac{1}{4}HI\)
\( \Rightarrow \Delta C'EF\) đồng dạng với \(\Delta CIH\) theo tỉ số đồng dạng \(k = \dfrac{1}{4} \Rightarrow \dfrac{{{S_{\Delta C'EF}}}}{{{S_{\Delta CIH}}}} = \dfrac{1}{{16}}\)
$\begin{array}{l}\dfrac{{NC'}}{{NC}} = \dfrac{{EC'}}{{HC}} = \dfrac{1}{4} \Rightarrow \dfrac{{d\left( {N';\left( {C'EF} \right)} \right)}}{{d\left( {N;\left( {CIH} \right)} \right)}} = \dfrac{1}{4}\\ \Rightarrow {V_{N.EFC'}} = \dfrac{1}{{16}}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{{64}}{V_{N.CIH}}\\{V_{LABH}} = {V_{M.ADI}} = \dfrac{1}{2}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{8}{V_{N.CIH}}\\ \Rightarrow {V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}} = \dfrac{{47}}{{64}}{V_{N.CIH}}\end{array}$
Ta có :
\(\begin{array}{l}\dfrac{{CC'}}{{NC}} = \dfrac{3}{4},\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = \dfrac{1}{2} \Rightarrow \dfrac{{{V_{ABCD.A'B'C'D'}}}}{{{V_{S.CIH}}}} = \dfrac{{d\left( {C';\left( {ABCD} \right)} \right).{S_{ABCD}}}}{{\dfrac{1}{3}d\left( {N;\left( {CIH} \right)} \right).{S_{CIH}}}} = 3.\dfrac{{CC'}}{{NC}}.\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = 3.\dfrac{3}{4}.\dfrac{1}{2} = \dfrac{9}{8}\\ \Rightarrow {V_{S.CIH}} = \dfrac{8}{9}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_{H'}} = \dfrac{{47}}{{64}}{V_{N.CIH}} = \dfrac{{47}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_H} = \dfrac{{25}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow \dfrac{{{V_H}}}{{{V_{H'}}}} = \dfrac{{25}}{{47}}\end{array}\)
Đáp án : A








Danh sách bình luận