Xét khối tứ diện $ABCD$ có cạnh $AD, BC$ thỏa mãn $A{B^2} + C{D^2} = 18$ và các cạnh còn lại đều bằng $5.$ Biết thể tích của khối tứ diện $ABCD $ đạt giá trị lớn nhất có dạng ${V_{\max }} = \dfrac{{x\sqrt y }}{4};\,\,x,y \in {N^*};\,\,(x;y) = 1$. Khi đó, $x,\,y$ thỏa mãn bất đẳng thức nào dưới đây?
-
A.
$x + {y^2} - xy > 4550$.
-
B.
$xy + 2x + y > 2550$.
-
C.
${x^2} - xy + {y^2} < 5240$
-
D.
${x^3} - y > 19602$.
Sử dụng bất đẳng thức Cô si: $2ab \le {a^2} + {b^2},\,\,\left( {a,b > 0} \right)$
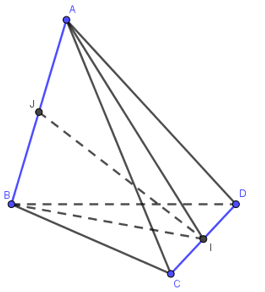
Gọi $I, J$ lần lượt là trung điểm $CD, AB$; độ dài các đoạn $AB = a,\,\,CD = b,\,\,a,b > 0,\,\,{a^2} + {b^2} = 18$
Tam giác $ACD$ và tam giác $ BCD$ cân tại $A, B$
$ \Rightarrow AI \bot CD,\,\,BI \bot CD \Rightarrow CD \bot (ABI)$
$ \Rightarrow {V_{ABCD}} = {V_{D.ABI}} + {V_{C.ABI}} $ $= \dfrac{1}{3}.DI.{S_{ABI}} + \dfrac{1}{3}.IC.{S_{ABI}} = \dfrac{1}{3}.CD.{S_{ABI}}$ (*)
Tam giác $AID$ vuông tại $I $ $ \Rightarrow AI = \sqrt {A{D^2} - I{D^2}} = \sqrt {{5^2} - {{\left( {\dfrac{b}{2}} \right)}^2}} = \sqrt {25 - \dfrac{{{b^2}}}{4}} $
Dễ dàng chứng minh $\Delta ACD = \Delta BCD\,\,(c.c.c) \Rightarrow IA = IB$ (Chiều cao tương ứng bằng nhau)
$ \Rightarrow \Delta IAB$ cân tại $I $ $ \Rightarrow IJ \bot AB$
Tam giác $AIJ$ vuông tại $J $ $ \Rightarrow IJ = \sqrt {A{I^2} - A\,{J^2}} = \sqrt {25 - \dfrac{{{b^2}}}{4} - \dfrac{{{a^2}}}{4}} = \sqrt {25 - \dfrac{{{b^2} + {a^2}}}{4}} = \sqrt {25 - \dfrac{{18}}{4}} = \dfrac{{\sqrt {82} }}{2}$
Diện tích tam giác $IAB: $ ${S_{IAB}} = \dfrac{1}{2}.AB.IJ = \dfrac{1}{2}.a.\dfrac{{\sqrt {82} }}{2} = \dfrac{{a\sqrt {82} }}{4}$.
Thay vào (*):
$\begin{array}{l}{V_{ABCD}} = \dfrac{1}{3}.b.\dfrac{{a\sqrt {82} }}{4} = \dfrac{{ab\sqrt {82} }}{{12}}\mathop \le \limits^{Co\,si} \dfrac{{\sqrt {82} }}{{12}}.\dfrac{{{a^2} + {b^2}}}{2} = \dfrac{{\sqrt {82} }}{{12}}.\dfrac{{18}}{2} = \dfrac{{3\sqrt {82} }}{4} = \dfrac{{x\sqrt[{}]{y}}}{4};\,\,x,y \in {N^*};\,\,(x;y) = 1\\ \Rightarrow x = 3,\,\,y = 82\end{array}$
Kiểm tra các biểu thức của từng phương án, ta thấy phương án A là đúng.
Đáp án : A
Các bài tập cùng chuyên đề
Cho khối chóp tứ giác $S.ABCD.$ Mặt phẳng đi qua trọng tâm các tam giác \(SAB,\;SAC,\;\;SAD\) chia khối chóp này thành hai phần có thể tích là \({V_1}\) và \({V_2}\;\;\left( {{V_1} < {V_2}} \right).\) Tính tỉ lệ \(\dfrac{{{V_1}}}{{{V_2}}}.\)
Cho hình hộp đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$ và $\widehat {BAD} = {60^0}$, $AB’$ hợp với đáy $(ABCD)$ một góc ${30^0}$. Thể tích của khối hộp là
Cho khối chóp $S.ABC$ có điểm $M$ và $N$ lần lượt nằm trên các cạnh $SA$ và $SB$ sao cho $\dfrac{{SM}}{{SA}} = \dfrac{1}{3},\,\dfrac{{SN}}{{SB}} = \dfrac{2}{3}$. Mặt phẳng $\left( \alpha \right)$ qua hai điểm $M, N$ và song song $SC$ chia khối chóp thành $2$ khối đa diện. Tính tỉ số thể tích của khối đa diện có thể tích lớn hơn so với thể tích khối chóp $S.ABC.$
Cho hình chóp tứ giác đều $S.ABCD,$ đường cao $SO.$ Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa $SO,$ thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng $a,$ tính thể tích khối chóp đã cho.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$, $AB = a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Mặt phẳng qua $A$ vuông góc với $SC$ cắt hình chóp theo một thiết diện. Tính diện tích thiết diện đó.
Cho hình hộp $ABCD.A’B’C’D’$ có tất cả các cạnh bằng $a,$ hình chiếu vuông góc của $A’$ lên mặt phẳng $(ABCD)$ nằm trong tứ giác $ABCD,$ các cạnh xuất phát từ đỉnh $A$ của hình hộp tạo với nhau một góc $60^0.$ Tính thể tích khối hộp $ABCD.A’B’C’D’.$
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(SA = SB = SC = a\). Thể tích lớn nhất của khối chóp \(S.ABCD\) là:
Cho hình chóp \(S.ABC\) có \(AB = 3,BC = 4,AC = 5\). Tính thể tích khối chóp \(S.ABC\) biết rằng cắc mặt bên tạo với đáy một góc \({30^0}\) và hình chiếu vuông góc của \(S\) trên \(\left( {ABC} \right)\) nằm trong tam giác \(ABC\)
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(E,F\) lần lượt là trung điểm của \(B'C'\) và \(C'D'\). Mặt phẳng \(\left( {AEF} \right)\) chia hình hộp thành hai hình đa diện \(\left( H \right)\) và \(\left( {H'} \right)\) trong đó \(\left( H \right)\) là hình đa diện chứa đỉnh \(A'\). Tính tỉ số thể tích đa diện \(\left( H \right)\) và thể tích hình đa diện \(\left( {H'} \right)\).
Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc $45^0$ và khoảng cách từ chân đường cao đến mặt bên bằng \(a\). Tính thể tích của khối chóp đó.
