Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(SA = SB = SC = a\). Thể tích lớn nhất của khối chóp \(S.ABCD\) là:
-
A.
\(\dfrac{{{a^3}}}{4}\)
-
B.
\(\dfrac{{3{a^3}}}{8}\)
-
C.
\(\dfrac{{{a^3}}}{8}\)
-
D.
\(\dfrac{{{a^3}}}{2}\)
Thể tích khối chóp \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
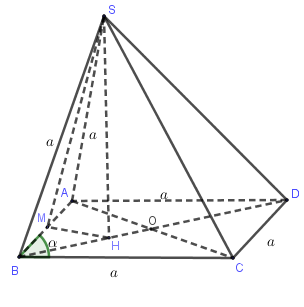
Gọi \(M\) là trung điểm của \(AB\), \(O\) là giao điểm của \(AC\) và \(BD\).
Qua \(M\) kẻ đường thẳng vuông góc với \(AB\) và cắt \(BO\) tại\(H\).
Khi đó \(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
Vì \(SA = SB = SC\) nên \(SH \bot \left( {ABC} \right)\).
Đặt \(\widehat {ABC} = \alpha \) ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \alpha \\ = {a^2} + {a^2} - 2{a^2}\cos \alpha = 2{a^2}\left( {1 - \cos \alpha } \right)\\ \Rightarrow A{O^2} = \dfrac{{A{C^2}}}{4} = \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2}\end{array}\)
Tam giác \(AOB\) vuông tại \(O\) nên:\(O{B^2} = A{B^2} - A{O^2} = {a^2} - \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2} = \dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}\)
Xét tam giác \(\Delta BHM \sim \Delta BAO\left( {g.g} \right)\) nên \(\dfrac{{MH}}{{AO}} = \dfrac{{BM}}{{BO}} \Rightarrow MH = \dfrac{{AO.BM}}{{BO}}\)
\( \Rightarrow M{H^2} = \dfrac{{A{O^2}.B{M^2}}}{{B{O^2}}} = \dfrac{{\dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2}.\dfrac{{{a^2}}}{4}}}{{\dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}}} = \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{{4\left( {1 + \cos \alpha } \right)}}\)
Tam giác \(SMH\) vuông tại \(H\) có \(S{H^2} = S{M^2} - M{H^2} = \dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{{4\left( {1 + \cos \alpha } \right)}} = \dfrac{{{a^2}}}{4}\left( {3 - \dfrac{{1 - \cos \alpha }}{{1 + \cos \alpha }}} \right) = \dfrac{{{a^2}}}{4}.\dfrac{{2 + 4\cos \alpha }}{{1 + \cos \alpha }} = \dfrac{{{a^2}\left( {1 + 2\cos \alpha } \right)}}{{2\left( {1 + \cos \alpha } \right)}}\)
\({S_{ABCD}} = 2{S_{ABC}} = BO.AC \Rightarrow S_{ABCD}^2 = B{O^2}.A{C^2} = \dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}.2{a^2}\left( {1 - \cos \alpha } \right) = {a^4}\left( {1 + \cos \alpha } \right)\left( {1 - \cos \alpha } \right)\)
\(\begin{array}{l} \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SH\\ \Rightarrow V_{S.ABCD}^2 = \dfrac{1}{9}S_{ABCD}^2.S{H^2} = \dfrac{1}{9}{a^4}\left( {1 + \cos \alpha } \right)\left( {1 - \cos \alpha } \right).\dfrac{{{a^2}\left( {1 + 2\cos \alpha } \right)}}{{2\left( {1 + \cos \alpha } \right)}} = \dfrac{{{a^6}\left( {1 - \cos \alpha } \right)\left( {1 + 2\cos \alpha } \right)}}{{18}}\end{array}\)
Đặt \(t = \cos \alpha \left( {t \in \left[ { - 1;1} \right]} \right)\) và xét hàm \(f\left( t \right) = \left( {1 - t} \right)\left( {1 + 2t} \right) = - 2{t^2} + t + 1\) trên \(\left[ { - 1;1} \right]\) có:
Hàm bậc hai \(f\left( t \right) = - 2{t^2} + t + 1\) có đồ thị là parabol với bề lõm hướng xuống dưới.
Do đó nó đạt GTLN tại \(t = \dfrac{1}{4}\) và \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = f\left( {\dfrac{1}{4}} \right) = \dfrac{9}{8}\).
Khi đó \(V_{\max }^2 = \dfrac{{{a^6}}}{{18}}.\dfrac{9}{8} = \dfrac{{{a^6}}}{{16}} \Rightarrow V = \dfrac{{{a^3}}}{4}\)
Đáp án : A








Danh sách bình luận