Cho tam giác ABC có \(\widehat {ABC} = 53^\circ ,\widehat {BAC} = 90^\circ \) , AH vuông góc với BC (H thuộc BC). Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho BD = HA (Hình 23).
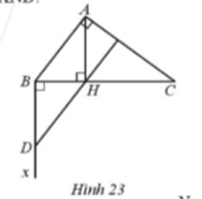
a) Chứng minh ∆AHB = ∆DBH.
b) Chứng minh DH vuông góc với AC.
c) Tính số đo góc BDH.
- Xét các điều kiện về cạnh và góc để chứng minh ∆AHB = ∆DBH
- Từ đó suy ra các góc tương ứng bằng nhau để chứng minh DH vuông góc với AC và tính số đo góc BDH.
a) Xét ∆AHB và ∆DBH có:
\(\widehat {AHB} = \widehat {HB{\rm{D}}}\) (cùng bằng 90°),
BH là cạnh chung,
AH = BD (giả thiết),
Suy ra ∆AHB = ∆DBH (hai cạnh góc vuông).
Vậy ∆AHB = ∆DBH.
b) Do ∆AHB = ∆DBH (chứng minh câu a) nên \(\widehat {ABH} = \widehat {DHB}\) (hai góc tương ứng).
Mà \(\widehat {ABH},\widehat {DHB}\) ở vị trí so le trong
Do đó AB // DH.
Lại có, AB ⊥ AC nên DH ⊥ AC (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).
Vậy DH ⊥ AC.
c) Do ∆AHB = ∆DBH (chứng minh câu a) nên\(\widehat {BAH} = \widehat {HDB}\) (hai góc tương ứng).
Xét tam giác ABH vuông tại H có:
\(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {BAH} = 90^\circ - \widehat {ABH} = 90^\circ - 53^\circ = 37^\circ \).
Do đó \(\widehat {BDH} = 37^\circ \).
Vậy \(\widehat {BDH} = 37^\circ \)

Các bài tập cùng chuyên đề
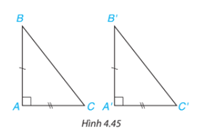
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A'B'C' bằng nhau.
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng \(\Delta ABM = \Delta DCM\).
Cho các điểm A, B, C, D như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED. Chứng minh rằng:
a) \(\Delta AED = \Delta BEC\)
b) \(\Delta ABC = \Delta BAD\)

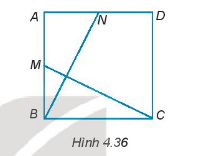
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng \(BN = CM;BN \bot CM.\)
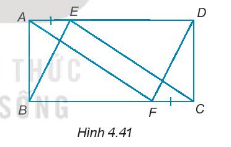
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy 2 điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
a) \(AF = CE\)
b) \(AF // CE\)
Cho 5 điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE
a) Chứng minh rằng AB = CE
b) Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = {90^0}\)

Cho hình chữ nhật ABCD. Cho M là trung điểm của cạnh BC. Chứng minh rằng \(\Delta ABM = \Delta DCM\).
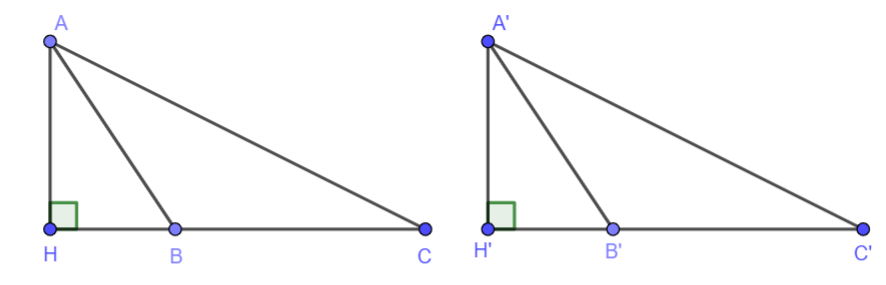
Cho hình vẽ dưới đây. Biết AB = A’B’, HB = H’B’, BC = B’C’.
Chứng minh rằng AC = A’C’.
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?
a) ΔAED = ΔACB.
b) DE = BC.
c) ΔACE = ΔABD.
d) \(\widehat {ABC} = \widehat {A{\rm{ED}}}\)







Danh sách bình luận