Cho các điểm A, B, C, D như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED. Chứng minh rằng:
a) \(\Delta AED = \Delta BEC\)
b) \(\Delta ABC = \Delta BAD\)

Chứng minh các tam giác trên bằng nhau theo trường hợp c – g – c .
a) Xét \(\Delta AED\) và \(\Delta BEC\) có:
\(\begin{array}{l}\widehat {AED} = \widehat {BEC} (= {90^\circ})\\EA = EB\left( {gt} \right)\\ED = EC\left( {gt} \right)\\ \text{Vậy } \Delta AED = \Delta BEC\left( {c - g - c} \right)\end{array}\)
b) Vì \(\Delta AED = \Delta BEC\left( {cmt} \right)\) nên \(AD = BC\) (2 cạnh tương ứng); \(\widehat {ADE} = \widehat {BCE}\) (2 góc tương ứng)
Vì \(AC = EC + EA\) và \(BD = ED + EB\)
Mà \(EC=ED;EA=EB\)
Do đó \(AC = BD\)
Xét \(\Delta ABC\) và \(\Delta BAD\) có:
\(\begin{array}{l}CB = DA(cmt)\\\widehat {BCA} = \widehat {ADB}\left( {cmt} \right)\\ AC = BD(cmt)\\ \text{Vậy } \Delta ABC = \Delta BAD\left( {c - g - c} \right)\end{array}\)

Các bài tập cùng chuyên đề
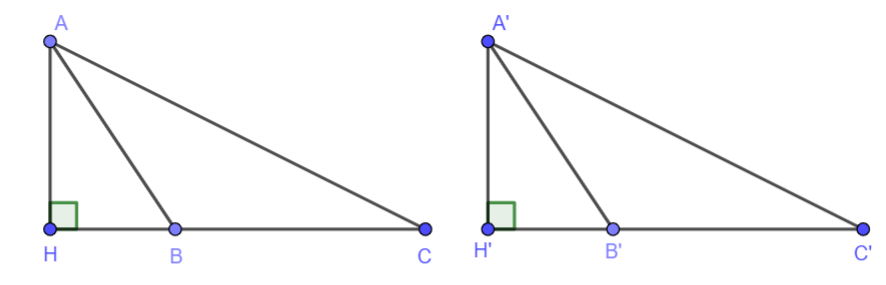
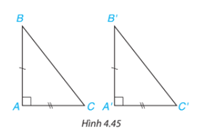
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A'B'C' bằng nhau.
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng \(\Delta ABM = \Delta DCM\).
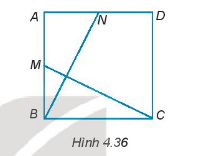
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng \(BN = CM;BN \bot CM.\)
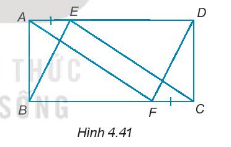
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy 2 điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
a) \(AF = CE\)
b) \(AF // CE\)
Cho 5 điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE
a) Chứng minh rằng AB = CE
b) Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = {90^0}\)

Cho hình chữ nhật ABCD. Cho M là trung điểm của cạnh BC. Chứng minh rằng \(\Delta ABM = \Delta DCM\).
Cho hình vẽ dưới đây. Biết AB = A’B’, HB = H’B’, BC = B’C’.
Chứng minh rằng AC = A’C’.
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?
a) ΔAED = ΔACB.
b) DE = BC.
c) ΔACE = ΔABD.
d) \(\widehat {ABC} = \widehat {A{\rm{ED}}}\)
Cho tam giác ABC có \(\widehat {ABC} = 53^\circ ,\widehat {BAC} = 90^\circ \) , AH vuông góc với BC (H thuộc BC). Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho BD = HA (Hình 23).
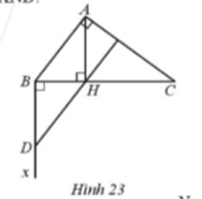
a) Chứng minh ∆AHB = ∆DBH.
b) Chứng minh DH vuông góc với AC.
c) Tính số đo góc BDH.







Danh sách bình luận