Cho hai đa thức \(A = {x^5} + 3{x^4} - 7{x^2} + x - 2\) cho \(B = {x^3} + 3{x^2} - 1\).
a) Bằng cách đặt tính chia, hãy tìm thương và dư trong phép chia A cho B.
b) Em có cách nào không cần thực hiện phép chia mà vẫn tìm được đa thức dư hay không?
a) Muốn chia một đa thức cho một đa thức, ta đặt tính và tiến hành chia (tương tự phép chia hai số tự nhiên) cho đến khi nhận được đa thức dư hoặc đa thức không, hoặc có bậc nhỏ hơn bậc của đa thức chia.
b) Viết biểu thức A dưới dạng: \(A = B.{x^2} + R\left( x \right)\), khi đó R(x) là đa thức dư của phép chia A cho B.
a) Ta đặt tính chia như sau:
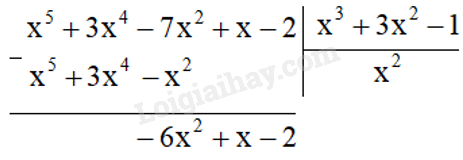
Vậy trong phép chia A cho B ta được thương là \({x^2}\) và dư là \( - 6{x^2} + x - 2\).
b) Không cần thực hiện phép chia, ta có thể tìm được thương và dư của phép chia này bằng cách biến đổi đa thức A như sau:
\(A = {x^5} + 3{x^4} - 7{x^2} + x - 2\)
\(A = \left( {{x^5} + 3{x^4} - {x^2}} \right) - 6{x^2} + x - 2\) (vì \( - 7{x^2} = - {x^2} - 6{x^2}\))
\(A = \left( {{x^3} + 3{x^2} - 1} \right){x^2} + \left( { - 6{x^2} + x - 2} \right)\) (vì \({x^5} + 3{x^4} - {x^2} = \left( {{x^3} + 3{x^2} - 1} \right){x^2}\))
\(A = B.{x^2} + \left( { - 6{x^2} + x - 2} \right)\)
Trong đẳng thức cuối, đa thức \( - 6{x^2} + x - 2\) có bậc 2 nhỏ hơn bậc của đa thức B.
Điều đó chứng tỏ \({x^2}\) là thương và \( - 6{x^2} + x - 2\) là dư trong phép chia A cho B.

Các bài tập cùng chuyên đề
Hãy mô tả lại các bước đã thực hiện trong phép chia đa thức D cho đa thức E
Kí hiệu dư thứ hai là G = - 6x + 10 . Đa thức này có bậc bằng 1. Lúc này phép chia có thể tiếp tục được không? Vì sao?
Hãy kiểm tra lại đẳng thức D = E . (5x – 3) + G
Tìm dư R và thương Q trong phép chia đa thức A= 3x4 – 6x – 5 cho đa thức B = x2 + 3x – 1 rồi viết A dưới dạng A = B . Q + R
Em có biết tại sao Vuông làm nhanh thế không?
Thực hiện phép chia 0,5x5 + 3,2x3 – 2x2 cho 0,25xn trong mỗi trường hợp sau:
a) n = 2
b) n = 3
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:
F(x) = G(x) . Q(x) + R(x)
a) F(x) = 6x4 – 3x3 + 15x2 + 2x – 1 ; G(x) = 3x2
b) F(x) = 12x4 + 10x3 – x – 3 ; G(x) = 3x2 + x + 1
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức 21x – 4 cho 3x2 . Em có thể giúp bạn Tâm được không?
Thực hiện phép chia \(({x^2} + 5x + 9):(x + 2)\)
Thực hiện phép chia.
a) \((4{x^2} - 5):(x - 2)\)
b) \((3{x^3} - 7x + 2):(2{x^2} - 3)\)
Thực hiện phép chia.
a) \((2{y^4} - 13{y^3} + 15{y^2} + 11y - 3):({y^2} - 4y - 3)\)
b) \((5{x^3} - 3{x^2} + 10):({x^2} + 1)\)
Tính:
a) \(({x^3} + 1):({x^2} - x + 1)\);
b) \((8{x^3} - 6{x^2} + 5):({x^2} - x + 1)\).
Tính:
a) \((6{x^2} - 2x + 1):(3x - 1)\);
b) \((27{x^3} + {x^2} - x + 1):( - 2x + 1)\);
c) \((8{x^3} + 2{x^2} + x):(2{x^3} + x + 1)\);
d) \((3{x^4} + 8{x^3} - 2{x^2} + x + 1):(3x + 1)\)
Cho hai đa thức \(A = 3{x^4} + {x^3} + 6x - 5;B = {x^2} + 1\). Tìm thương Q và dư R trong phép chia A cho B rồi kiểm nghiệm lại rằng A = BQ + R.
Thực hiện các phép chia sau:
a) \(\left( {2{x^4} + {x^3} - 3{x^2} + 5x - 2} \right):\left( {{x^2} - x + 1} \right)\)
b) \(\left( {{x^4} - {x^3} - {x^2} + 3x} \right):\left( {{x^2} - 2x + 3} \right)\)
Thực hiện phép chia.
a) \(\left( {2{x^2} - 7x + 4} \right):\left( {x - 2} \right)\)
b) \(\left( {2{x^3} + 3{x^2} + 3x + 4} \right):\left( {{x^2} + 2} \right)\)
Tính:
a) \((3{x^3} - 7{x^2} + 4x - 4):(x - 2)\)
b) \(({x^5} + x + 1):({x^3} - x)\)
a) Tìm số dư của phép chia đa thức 4x4 – 2x2 +7 cho x + 3
b) Tìm đa thức bị chia, biết đa thức chia là x2 – 2x + 3, thương là x2 − 2, dư là 9x – 5
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: \(F\left( x \right) = G\left( x \right).Q\left( x \right) + R\left( x \right)\).
a) \(F\left( x \right) = 6{x^4} - 3{x^3} + 15{x^2} + 2x - 1;G\left( x \right) = 3{x^2}\).
b) \(F\left( x \right) = 12{x^4} + 10{x^3} - x - 3;G\left( x \right) = 3{x^2} + x + 1\).
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức \(21x - 4\) cho \(3{x^2}\). Em có thể giúp bạn Tâm được không?
Tìm số b sao cho đa thức \({x^3} - 3{x^2} + 2x - b\) chia hết cho đa thức \(x - 3\).








Danh sách bình luận