Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn đến chữ số thập phân thứ tư):
a) \({15^{\frac{2}{5}}}\);
b) \({20^{\frac{{ - 1}}{2}}}\);
c) \(5,{7^{2,4}}\);
d) \(0,{45^{ - 2,38}}\).
Sử dụng máy tính cầm tay để tính.
a) Nhập vào máy tính:

Ta thu được kết quả
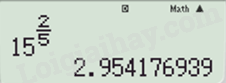
\({15^{\frac{2}{5}}} \approx 2,9542\);
b) Nhập vào máy tính:

Ta thu được kết quả
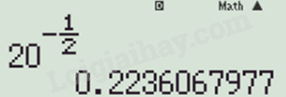
\({20^{\frac{{ - 1}}{2}}} \approx 0,2236\);
c) Nhập vào máy tính:

Ta thu được kết quả
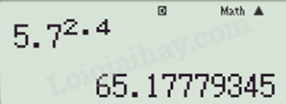
\(5,{7^{2,4}} \approx 65,1778\);
d) Nhập vào máy tính:

Ta thu được kết quả
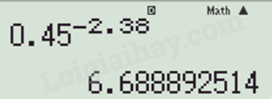
\(0,{45^{ - 2,38}} = 6,6889\).

Các bài tập cùng chuyên đề
Rút gọn biểu thức: \(A = \frac{{{x^{\frac{3}{2}}}y + x{y^{\frac{3}{2}}}}}{{\sqrt x + \sqrt y }}\,\,\,\left( {x,y > 0} \right).\)
Cho a là một số thực dương.
a) Với n là số nguyên dương, hãy thử định nghĩa \({a^{\frac{1}{n}}}\) sao cho \({\left( {{a^{\frac{1}{n}}}} \right)^n} = a.\)
b) Từ kết quả của câu a, hãy thử định nghĩa \({a^{\frac{m}{n}}},\) với m là số nguyên và n là số nguyên dương, sao cho \({a^{\frac{m}{n}}} = {\left( {{a^{\frac{1}{n}}}} \right)^m}.\)
Câu hỏi: Vì sao trong định nghĩa lũy thừa với số mũ hữu tỉ lại cần điều kiện cơ số a > 0?
Rút gọn biểu thức \(\sqrt {x\sqrt {x\sqrt x } } :{x^{\frac{5}{8}}}(x > 0)\) ta được
A. \(\sqrt[4]{x}\)
B. \(\sqrt x \).
C. \(\sqrt[3]{x}\).
D. \(\sqrt[5]{x}\)
Viết các biểu thức sau dưới dạng luỹ thừa với số mũ hữu tỉ:
a) \(\sqrt {{2^3}} \);
b) \(\sqrt[5]{{\frac{1}{{27}}}}\);
c) \({\left( {\sqrt[5]{a}} \right)^4}\).
Tính giá trị các biểu thức sau:
a) \({25^{\frac{1}{2}}}\);
b) \({\left( {\frac{{36}}{{49}}} \right)^{ - \frac{1}{2}}}\);
c) \({100^{1,5}}\).
Viết các biểu thức sau dưới dạng một luỹ thừa \(\left( {a > 0} \right)\):
a) \(3.\sqrt 3 .\sqrt[4]{3}.\sqrt[8]{3}\);
b) \(\sqrt {a\sqrt {a\sqrt a } } \);
c) \(\frac{{\sqrt a .\sqrt[3]{a}.\sqrt[4]{a}}}{{{{\left( {\sqrt[5]{a}} \right)}^3}.{a^{\frac{2}{5}}}}}\).
Thực hiện các hoạt động sau:
a) So sánh: \({2^{\frac{6}{3}}}\) và \({2^2}\).
b) So sánh: \({2^{\frac{6}{3}}}\) và \(\sqrt[3]{{{2^6}}}\).
Điều kiện xác định của \(\sqrt[5]{{{x^3}}}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ne 0\)
C. \(x \ge 0\)
D. \(x > 0\)
Điều kiện xác định của \(\sqrt[8]{{{x^3}}}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ne 0\)
C. \(x \ge 0\)
D. \(x > 0\)
Không sử dụng máy tính cầm tay, tính giá trị của các biểu thức sau:
a) \({8^{ - \frac{2}{3}}}\);
b) \({32^{ - \frac{2}{5}}}\);
c) \({81^{1,25}}\);
d) \(1\;{000^{ - \frac{5}{3}}}\);
e) \({\left( {\frac{{16}}{{81}}} \right)^{ - \frac{1}{4}}}\);
g) \({\left( {\frac{8}{{27}}} \right)^{ - \frac{2}{3}}}\).
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,(a,b > 0)$ ta được:
-
A.
$P = \sqrt[3]{a} + \sqrt[3]{b}$
-
B.
$P = a + b$
-
C.
\(P = a - b\)
-
D.
$P = \sqrt[3]{a} - \sqrt[3]{b}$
Rút gọn biểu thức \(P=\sqrt{a.\sqrt[3]{{{a}^{2}}.\sqrt[4]{\frac{1}{a}}}}:\sqrt[24]{{{a}^{7}}},\ \ \left( a>0 \right)\) ta được biểu thức dạng \({{a}^{\frac{m}{n}}},\) trong đó \(\frac{m}{n}\) là phân số tối giản, \(m,\ \ n\in {{N}^{*}}.\) Tính giá trị \({{m}^{2}}+{{n}^{2}}.\)
-
A.
10
-
B.
25
-
C.
5
-
D.
13
Biểu thức thu gọn của biểu thức \(P\) có dạng \(P = \dfrac{m}{{a + n}}\). Khi đó biểu thức liên hệ giữa \(m\) và \(n\) là:
\(P = \left( {\dfrac{{{a^{\frac{1}{2}}} + 2}}{{a + 2{a^{\frac{1}{2}}} + 1}} - \dfrac{{{a^{\frac{1}{2}}} - 2}}{{a - 1}}} \right).\dfrac{{\left( {{a^{\frac{1}{2}}} + 1} \right)}}{{{a^{\frac{1}{2}}}}}\)
-
A.
\(m + 3n = 1\)
-
B.
\(m + n = - 2\)
-
C.
\(m - n = 0\)
-
D.
\(2m - n = 5\)
Với a là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
-
A.
\({a^{\frac{5}{2}}}\)
-
B.
\(a\)
-
C.
\({a^{\frac{3}{2}}}\)
-
D.
\({a^{\frac{1}{4}}}\)
Rút gọn biểu thức \(P = {x^2}.\sqrt[3]{x}\), x > 0.
-
A.
\(P = {x^{\frac{4}{3}}}\)
-
B.
\(P = {x^{\frac{5}{3}}}\)
-
C.
\(P = {x^{\frac{7}{3}}}\)
-
D.
\(P = {x^{\frac{8}{3}}}\)
Tập xác định của hàm số \(y = {\left( {x - 1} \right)^{\frac{1}{3}}}\) là
-
A.
\(\left[ {1; + \infty } \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\mathbb{R}\)
-
D.
Một đáp án khác
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có:
-
A.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[{nm}]{a}\).
-
B.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[m]{{{a^n}}}\).
-
C.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
-
D.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{\sqrt[m]{a}}}\).
Với a là số thực dương tuỳ ý, \(\sqrt {{a^3}} \) bằng
-
A.
\({a^{\frac{3}{2}}}\)
-
B.
\({a^{\frac{2}{3}}}\)
-
C.
\({a^6}\)
-
D.
\({a^{\frac{1}{6}}}\)
Rút gọn biểu thức \(P = {x^{\frac{2}{5}}}.\sqrt[6]{x}\) với x > 0.
-
A.
\(P = \sqrt x \)
-
B.
\(P = {x^{\frac{{17}}{{30}}}}\)
-
C.
\(P = {x^{\frac{1}{{15}}}}\)
-
D.
\(P = {x^{\frac{{17}}{{15}}}}\)
Cho biểu thức \(T = {x^{ - \frac{3}{4}}}\sqrt[4]{{{x^5}}}\) \((x > 0)\). Khẳng định nào sau đây đúng?
-
A.
\( T = x^{-\frac{1}{2}} \).
-
B.
\( T = x^{-2} \).
-
C.
\( T = x^{\frac{1}{2}} \).
-
D.
\( T = x^{2} \).
Với a là số thực dương tùy ý, biểu thức $a^{\dfrac{7}{2}}.a^{\dfrac{3}{2}}$ bằng
-
A.
$a^{\dfrac{{}^{5}}{9}}$.
-
B.
$a^{2}$.
-
C.
$a^{5}$.
-
D.
$a^{\dfrac{4}{3}}$.







Danh sách bình luận