Hình thoi có tính chất gì? - Toán 8

Hình thoi là tứ giác có bốn cạnh bằng nhau.

Hình thoi cũng là một hình bình hành.

Ví dụ:

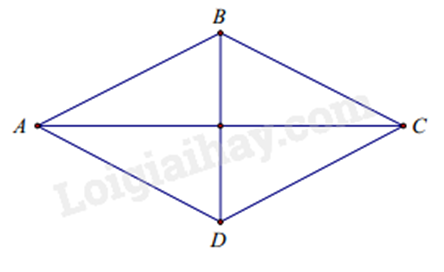
Xét hình thoi ABCD có:

+ Bốn cạnh bằng nhau: AB = BC = CD = DA .

+ Hai góc đối nhau: \(\widehat A\) và \(\widehat C\); \(\widehat B\) và \(\widehat D\).

+ Hai đường chéo: AC và BD .

+ Hai cạnh đối nhau: AB và CD ; BC và AD .

Trong hình thoi:

+ Các cạnh đối song song;

+ Các góc đối bằng nhau;

+ Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

+ Hai đường chéo là các đường phân giác của các góc ở đỉnh.

+ Hình thoi có đầy đủ tính chất của hình bình hành.

Ví dụ:

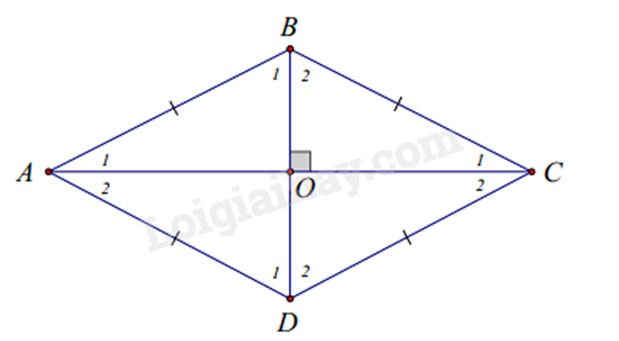
Xét hình thoi ABCD có \(O\) là giao điểm hai đường chéo, ta có:

+ Các cạnh đối song song: \(AB\parallel BC\) và \(BC\parallel DA\).

+ Các góc đối bằng nhau: \(\hat A = \hat B\) và \(\hat B = \hat D\).

+  Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường: \(AC \bot BD\) và \(OA = OC;OB = OD\).

+ Hai đường chéo là các đường phân giác của các góc ở đỉnh: \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\) và \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\).