Giải tam giác là gì? Cách giải tam giác - Toán 10

Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi đã biết một số yếu tố của tam giác đó.

Muốn giải tam giác ta cần tìm mối liên hệ giữa các góc, cạnh đã cho với các góc, các cạnh chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.

Có 3 bài toán cơ bản về gỉải tam giác:

a) Giải tam giác khi biết một cạnh và hai góc

=> Dùng định lí sin để tính cạnh còn lại.

b) Giải tam giác khi biết hai cạnh và góc xen giữa

=> Dùng định lí cosin để tính cạnh thứ ba. 

Sau đó dùng hệ quả của định lí cosin để tính góc.

c) Giải tam giác khi biết ba cạnh

=> Dùng hệ quả của định lí cosin để tính góc.

Chú ý: 

- Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài.

- Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.

Định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\).

Hệ quả định lí cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\).

Định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).

1) Cho tam giác ABC có AB = 1, BC = 2, \(\widehat {ABC} = {60^o}\). Tính độ dài cạnh và số đo các góc còn lại của tam giác.

Giải:

Độ dài cạnh AC là:

Áp dụng định lý cosin, ta có:

\(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\)

\( \Rightarrow {\mkern 1mu} {\mkern 1mu} A{C^2} = 1 + 4 - 2.1.2.\cos {60^o} = 3\)

\( \Rightarrow {\mkern 1mu} {\mkern 1mu} AC = \sqrt 3 \).

Áp dụng định lý sin, ta có:

\(\left\{ \begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\\\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sin A = \frac{{BC\sin B}}{{AC}} = \frac{{2\sin {{60}^o}}}{{\sqrt 3 }} = 1\\\sin C = \frac{{AB\sin B}}{{AC}} = \frac{{1\sin {{60}^o}}}{{\sqrt 3 }} = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}A = {90^o}\\C = {30^o}\end{array} \right.\)

2) Để đo chiều cao toà tháp người ta dùng dụng cụ đo góc có chiều cao 1,2 m đặt tại hai vị trí trên mặt đất cách nhau một khoảng AB = 30 m.  Tại vị trí A và B góc đo thu được so với phương ngang lần lượt là \(\alpha  = 65^o ;\beta  = 50^o \) (hình minh hoạ). Chiều cao h của toà tháp (từ điểm M tới mặt đất) là bao nhiêu?

Giải:

Xét tam giác \(MCE\) vuông tại \(E\) có: \(CE = \frac{{ME}}{{\tan \alpha }} = \frac{{h - 1,2}}{{\tan 65^o }}\).

Xét tam giác \(MED\) vuông tại \(E\) có: \(DE = \frac{{ME}}{{\tan \beta }} = \frac{{h - 1,2}}{{\tan 50^o }}\).

Ta có: \(CE + CD = DE \Leftrightarrow \frac{{h - 1,2}}{{\tan 65^o }} + 30 = \frac{{h - 1,2}}{{\tan 50^o }} \Rightarrow h \approx 81,7\) m.

3) Muốn đo chiều cao CD của một cái tháp mà ta không thể đến được tâm C của chân tháp. Trong mặt phẳng đứng chứa chiều cao CD của tháp ta chọn hai điểm A và B sao cho ba điểm A, B, C thẳng hàng. Giả sử ta đo được khoảng cách AB = 24 m và các góc \(\widehat {CAD} = {63^o}\), \(\widehat {CBD} = {48^o}\). Hãy tính chiều cao h = CD của tháp (kết quả làm tròn đến hàng phần mười).

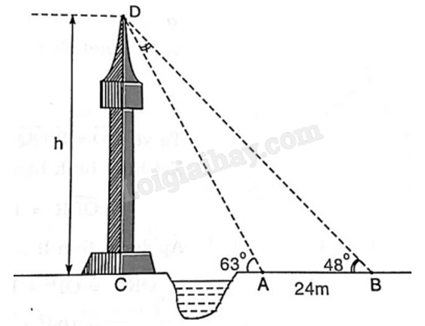
Giải:

+) \(\widehat {CAD} + \widehat {BAD} = {180^o} \Rightarrow \widehat {BAD} = {180^o} - \widehat {CAD} = {180^o} - {63^o} = {117^o}\).

+) Xét tam giác ABD có \(\widehat D = {180^o} - \widehat A - \widehat B = {180^o} - {117^o} - {48^o} = {15^o}\).

Áp dụng định lí sin cho tam giác ABD: \(\frac{{AB}}{{\sin \widehat {BDA}}} = \frac{{AD}}{{\sin \widehat {ABD}}}\).

Suy ra \(AD = \frac{{AB\sin \widehat {ABD}}}{{\sin \widehat {ADB}}} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\).

Xét tam giác ACD vuông tại C: \(\sin \widehat {CAD} = \frac{{CD}}{{AD}}\).

Suy ra \(CD = AD\sin \widehat {CAD} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\sin {63^o} \approx 61,4\) (m).