Giải bài 5 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau: Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2000 mg calcium, 3000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam mỗi loại thực phẩm X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?

Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa

Đề bài

Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau:

Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2000 mg calcium, 3000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam mỗi loại thực phẩm X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?

Phương pháp giải - Xem chi tiết

Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.

Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.

Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.

Lời giải chi tiết

Gọi \(x,y\) (\(x \ge 0,y \ge 0\), tính theo 100g) lần lượt là khối lượng thực phẩm X và Y cần chọn.

Cần cung cấp ít nhất 2000 mg calcium nên ta có \(200x + 500y \ge 2000\) hay \(2x + 5y - 20 \ge 0\).

Cần cung cấp ít nhất 3000 mg phosphorus nên ta có \(600x + 300y \ge 3000\) hay \(2x + y - 10 \ge 0\).

Cần cung cấp ít nhất 48 mg iron nên ta có \(8x + 6y \ge 48\) hay \(4x + 3y - 24 \ge 0\).

Khối lượng thực phẩm cần mua là \(F = 100\left( {x + y} \right)\) (nghìn đồng).

Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 100\left( {x + y} \right) \to \min \) với ràng buộc \(\left\{ \begin{array}{l}2x + 5y - 20 \ge 0\\2x + y - 10 \ge 0\\4x + 3y - 24 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)

Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).

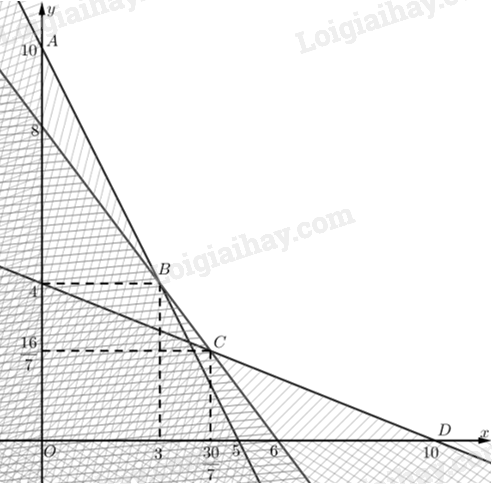
Ta có \(A\left( {0;10} \right),D\left( {10;0} \right)\).

Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x + y = 10\\4x + 3y = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 4\end{array} \right.\). Vậy \(B\left( {3;4} \right)\).

Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x+5y=20\\4x+3y=24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x=\frac{30}{7}\\y=\frac{16}{7}\end{array} \right.\). Vậy \(C\left( {\frac{{30}}{7};\frac{{16}}{7}} \right)\).

Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):

\(F\left( {0;10} \right) = 1000;F\left( {3;4} \right) = 700;F\left( {\frac{{30}}{7};\frac{{16}}{7}} \right) = \frac{{4600}}{7};F\left( {10;0} \right) = 1000\)

Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {\frac{{30}}{7};\frac{{16}}{7}} \right) = \frac{{4600}}{7}\).

Vậy cần mua \(\frac{{30}}{7}.100g = \frac{{3000}}{7}g \approx 429g\) thực phẩm X và \(\frac{{16}}{7}.100g = \frac{{1600}}{7}g \approx 229g\) thực phẩm Y để thực phẩm hỗn hợp có khối lượng nhỏ nhất.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Để làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh.
Giải bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Một cơ sở đóng thuyền thủ công cần 10 giờ lao động để đóng một thuyền loại A và 15 giờ lao động để đóng một thuyền loại B. Mỗi tuần cơ sở bố trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền này. Qua thực tế, người ta thấy mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B. Mỗi thuyền loại A, loại B cho lợi nhuận lần lượt là 0,5 triệu đồng và 0,7 triệu đồng. Mỗi tuần cơ sở nên đóng bao nhiêu thuyền mỗi loại để có thể thu được lợi nhuận cao nhất?
Giải bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Giải bài toán quy hoạch tuyến tính: (F = 10x + 20y to min ) với ràng buộc (left{ begin{array}{l}20{rm{x}} + 5y ge 40\16{rm{x}} + 60y ge 120\x - y le 3\x ge 0\y ge 0end{array} right.)
Giải bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Giải bài toán quy hoạch tuyến tính: (F = 8x + 5y to max ,min ) với ràng buộc (left{ begin{array}{l}2{rm{x}} + y le 8\x ge 0\x le 3\y ge 1\y le 5end{array} right.)
Giải mục 2 trang 11, 12, 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Xét tình huống thương nhân thu mua trái cây ở Bài toán mở đầu (trang 6). a) Nếu gọi (x,y) (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì (x) và (y) phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào? b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.
Giải mục 1 trang 6, 7, 8, 9, 10 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức (F = x + 2y) với (left( {x;y} right)) là nghiệm của hệ bất phương trình (left{ begin{array}{l}x - 2y + 4 ge 0x + y - 5 le 0x ge 0y ge 0end{array} right.) (I) Miền nghiệm ({Omega }) của hệ (I) là miền tứ giác (OABC) (được tô màu) trên Hình 1. Với giá trị (F) cho trước, xét đường thẳng (d:x + 2y - F = 0) hay (y = - frac{x}{2} + frac{F}{2}). Trả lời các câu hỏi sau để giải bài toán tr