Bài 1. Bài toán quy hoạch tuyến tính - Chuyên đề học tậ..

Giải bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo


Giải bài toán quy hoạch tuyến tính: (F = 10x + 20y to min ) với ràng buộc (left{ begin{array}{l}20{rm{x}} + 5y ge 40\16{rm{x}} + 60y ge 120\x - y le 3\x ge 0\y ge 0end{array} right.)

Đề bài

Giải bài toán quy hoạch tuyến tính:

\(F = 10x + 20y \to \min \)

với ràng buộc

\(\left\{ \begin{array}{l}20{\rm{x}} + 5y \ge 40\\16{\rm{x}} + 60y \ge 120\\x - y \le 3\\x \ge 0\\y \ge 0\end{array} \right.\)

Phương pháp giải - Xem chi tiết

Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).

Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).

Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).

Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).

Lời giải chi tiết

Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).

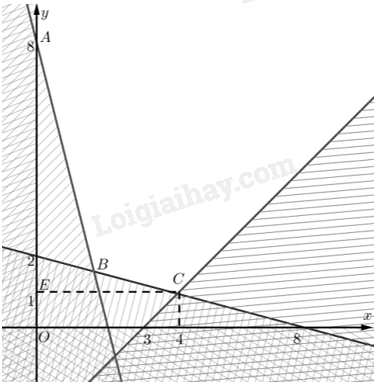
Ta có \(A\left( {0;8} \right)\).

Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}20{\rm{x}} + 5y = 40\\15{\rm{x}} + 60y = 120\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{8}{5}\\y = \frac{8}{5}\end{array} \right.\). Vậy \(B\left( {\frac{8}{5};\frac{8}{5}} \right)\).

Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x - y = 3\\15{\rm{x}} + 60y = 120\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right.\). Vậy \(C\left( {4;1} \right)\).

Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F = 10x + 20y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).

Ta có \(F\left( {0;8} \right) = 160;F\left( {\frac{8}{5};\frac{8}{5}} \right) = 48;F\left( {4;1} \right) = 60\).

Do đó \(F\) đạt giá trị nhỏ nhất tại đỉnh \(B\left( {\frac{8}{5};\frac{8}{5}} \right)\) và \(\mathop {\min }\limits_{\Omega } F = B\left( {\frac{8}{5};\frac{8}{5}} \right) = 48\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

    Một cơ sở đóng thuyền thủ công cần 10 giờ lao động để đóng một thuyền loại A và 15 giờ lao động để đóng một thuyền loại B. Mỗi tuần cơ sở bố trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền này. Qua thực tế, người ta thấy mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B. Mỗi thuyền loại A, loại B cho lợi nhuận lần lượt là 0,5 triệu đồng và 0,7 triệu đồng. Mỗi tuần cơ sở nên đóng bao nhiêu thuyền mỗi loại để có thể thu được lợi nhuận cao nhất?

  • Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

    Để làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh.

  • Giải bài 5 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

    Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau: Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2000 mg calcium, 3000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam mỗi loại thực phẩm X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?

  • Giải bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

    Giải bài toán quy hoạch tuyến tính: (F = 8x + 5y to max ,min ) với ràng buộc (left{ begin{array}{l}2{rm{x}} + y le 8\x ge 0\x le 3\y ge 1\y le 5end{array} right.)

  • Giải mục 2 trang 11, 12, 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

    Xét tình huống thương nhân thu mua trái cây ở Bài toán mở đầu (trang 6). a) Nếu gọi (x,y) (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì (x) và (y) phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào? b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store