Giải bài 35 trang 103 sách bài tập toán 8 - Cánh diều

Cho hình vuông \(ABCD\) có \(AB = 12cm\). Trên cạnh \(CD\) lấy điểm \(E\) sao cho \(DE = 5cm\). Tia phân giác của góc \(BAE\) cắt \(BC\) tại \(F\).

Đề bài

Cho hình vuông \(ABCD\) có \(AB = 12cm\). Trên cạnh \(CD\) lấy điểm \(E\) sao cho \(DE = 5cm\). Tia phân giác của góc \(BAE\) cắt \(BC\) tại \(F\). Trên tia đối của tia \(BC\) lấy điểm \(M\) sao cho \(BM = DE\).

a) Chứng minh \(AE = AM = DE\)

b) Tính độ dài \(BF\).

Phương pháp giải - Xem chi tiết

Trong một hình vuông,

- Các cạnh đối song song

- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

Lời giải chi tiết

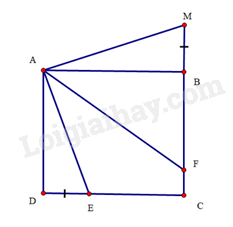
a) \(\Delta ADE = \Delta ABM\)(c.g.c)

Suy ra \(AE = AM\) và \(\widehat {DAE} = \widehat {BAM}\).

Do \(AF\) là tia phân giác của \(\widehat {BAE}\) nên \(\widehat {EAF} = \widehat {BAF}\).

Suy ra \(\widehat {DAE} + \widehat {EAF} = \widehat {BAM} + \widehat {BAF}\) hay \(\widehat {DAF} = \widehat {MAF}\).

Mà \(\widehat {DAF} = \widehat {MFA}\) (hai góc so le trong) , suy ra \(\widehat {MFA} = \widehat {MAF}\)

Do đó, tam giác \(MAF\) cân tại \(M\). Suy ra \(AM = FM\)

Mà \(AE = AM\), suy ra \(AE = AM = FM\).

b) Trong tam giác \(ADE\) vuông tại \(D\), ta có: \(A{E^2} = A{D^2} + D{E^2}\)

Suy ra \(AE = 13cm\). Mà \(FM = AE\), suy ra \(FM = 13cm\).

Ta có: \(FM = BM + BF\). Mà \(BM = DE = 5cm\) và \(FM = 13cm\), suy ra \(BF = 8cm\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 36 trang 103 sách bài tập toán 8 - Cánh diều
Cho hình vuông \(ABCD\). Lấy điểm \(E\) thuộc cạnh \(CD\) và điểm \(F\) thuộc tia đối của tia \(BC\) sao cho \(BF = DE\).
Giải bài 34 trang 102 sách bài tập toán 8 - Cánh diều
Cho tam giác \(ABC\) có các đường trung tuyến \(BD,CE\) cắt nhau tại \(G\). Gọi \(F,H\) lần lượt là trung điểm của \(BG,CG\).
Giải bài 33 trang 102 sách bài tập toán 8 - Cánh diều
Cho hình bình hành \(ABCD\). Ở phía ngoài hình bình hành, vẽ các hình vuông \(ABEF\) và \(ADGH\) (Hình 26). Chứng minh:
Giải bài 32 trang 102 sách bài tập toán 8 - Cánh diều
Cho hình chữ nhật \(ABCD\) có hai cạnh kề không bằng nhau. Tia phân giác của các góc \(A\) và \(B\) cắt nhau tại \(E\).
Giải bài 31 trang 102 sách bài tập toán 8 - Cánh diều
Cho hình vuông \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Trên tia đối của tia \(CB\) lấy điểm \(K\) sao cho \(BC = CK\).