Giải bài 3 trang 57 sách bài tập toán 8 - Chân trời sáng tạo

Cho tứ giác ABCD như Hình 12. a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

Cho tứ giác ABCD như Hình 12.

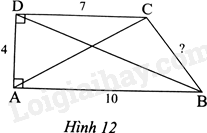
a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.

b) Cho biết góc B bằng \({53^0}\). Tìm số đo góc C.

Phương pháp giải - Xem chi tiết

a) Sử dụng kiến thức về định lí Pythagore vào tam giác vuông để tính: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

b) Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc C: Tổng số đo các góc của một tứ giác bằng 360 độ.

Lời giải chi tiết

a) Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:

\(A{C^2} = A{D^2} + D{C^2} = {4^2} + {7^2} = 65\), suy ra \(AC = \sqrt {65} \)

Áp dụng định lí Pythagore vào tam giác ADB vuông tại A có:

\(B{D^2} = A{D^2} + A{B^2} = {4^2} + {10^2} = 116\), suy ra \(BD = \sqrt {116} \)

Kẻ CE \( \bot \) AB. Do AD \( \bot \) AB suy ra CE // AD.

Suy ra \(\widehat {DAC} = \widehat {ACE}\) (hai góc so le trong)

Xét \(\Delta ADC\) và \(\Delta CEA\) có:

\(\widehat D = \widehat E = {90^o}\)

\(\widehat {DAC} = \widehat {ACE}\)(cmt)

AC chung

=> \(\Delta ADC\) = \(\Delta CEA\) (cạnh huyền – góc nhọn)

=> AD = CE = 4, DC = AE = 7 (các cặp cạnh tương ứng)

Ta có AE + EB = AB => EB = AB – AE = 10 – 7 = 3

Áp dụng định lí Pythagore vào tam giác CEB vuông tại E, ta có:

\(C{E^2} + E{B^2} = {4^2} + {3^2} = 25 = {5^2} = B{C^2}\), suy ra BC = 5

b) Tứ giác ABCD có: \(\widehat {DCB} = {360^0} - \widehat {DAB} - \widehat {ADC} - \widehat {ABC} = {360^0} - {90^0} - {90^0} - {53^0} = {127^0}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Bạn Hùng muốn làm một cái diều có dạng hình tứ giác KITE như Hình 13. Cho biết \(\widehat {KIT} = {90^0}\), \(\widehat {KET} = {70^0},\) \(IK = IT,\) \(EK = ET\).
Giải bài 5 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Cho tứ giác ABCD có \(\widehat C - \widehat D = {10^0}\). Các tia phân giác của góc A và góc B cắt nhau tại I. Biết \(\widehat {AIB} = {65^0}\). Tính góc C và góc D.
Giải bài 6 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Cho tứ giác ABCD có (AB = AD,CB = CD,widehat C = {65^0},widehat A = {115^0})
Giải bài 7 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết (BC = 15cm,CD = 24cm) và (AD = 20cm.) Tính độ dài AB.
Giải bài 8 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi tứ giác đó.
Giải bài 2 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Tìm số đo x trong các tứ giác sau:
Giải bài 1 trang 56 sách bài tập toán 8 - Chân trời sáng tạo
Tìm tứ giác lồi trong các hình sau: