Giải bài 29 trang 70 sách bài tập toán 8 – Cánh diều

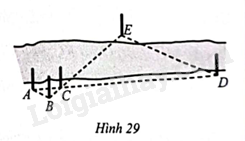
Để đo khoảng cách giữa hai địa điểm \(D,E\) ở hai bên bờ con sông, người ta chọn các vị trí \(A,B,C\) ở cùng một bên bờ với điểm \(D\) và đo được \(AB=2m,AC=3m,CD=15m\) (Hình 29). Giả sử \(\Delta ABC\backsim \Delta DEC\). Tính khoảng cách \(DE\).

Đề bài

Để đo khoảng cách giữa hai địa điểm \(D,E\) ở hai bên bờ con sông, người ta chọn các vị trí \(A,B,C\) ở cùng một bên bờ với điểm \(D\) và đo được \(AB=2m,AC=3m,CD=15m\) (Hình 29). Giả sử \(\Delta ABC\backsim \Delta DEC\). Tính khoảng cách \(DE\).

Phương pháp giải - Xem chi tiết

Dựa vào định nghĩa của tam giác đồng dạng:

Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:

\(\widehat{A'}=\widehat{A},\widehat{B'}=\widehat{B},\widehat{C'}=\widehat{C}\) ; \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}\).

Kí hiệu là \(\Delta A'B'C'\backsim \Delta ABC\).

Tỉ số các cạnh tương ứng \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=k\) gọi là tỉ số đồng dạng.

Lời giải chi tiết

Vì \(\Delta ABC\backsim \Delta DEC\) nên \(\frac{AB}{DE}=\frac{AC}{DC}\) hay \(\frac{AB}{AC}=\frac{DE}{DC}\).

→ \(\frac{2}{3}=\frac{DE}{15}\)

→ \(DE=\frac{2}{3}.15=10\) m.

Vậy \(DE=10\) m

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 30 trang 70 sách bài tập toán 8 – Cánh diều
Cho hình vuông \(ABCD\) cạnh bằng \(a\). Lấy điểm \(E\) thuộc cạnh \(BC\), điểm \(F\) thuộc cạnh \(AD\) sao cho \(CE=AF\). Các đường thẳng \(AE,BF\) cắt đường thẳng \(DC\) lần lượt tại \(M\) và \(N\).
Giải bài 28 trang 70 sách bài tập toán 8 – Cánh diều
Quan sát Hình 28 biết \(\widehat{AMN}=\widehat{ABC},\widehat{BAC}=\widehat{BML}\).
Giải bài 27 trang 70 sách bài tập toán 8 – Cánh diều
Cho \(\Delta ABC\backsim \Delta A'B'C'\) với tỉ số đồng dạng là 3. Tính các cạnh \(AB,BC,CA\) biết \(\frac{A'B'}{3}=\frac{B'C'}{7}=\frac{A'C'}{5}\) và \(A'B'+B'C'+C'A'=30\) (cm).
Giải bài 26 trang 70 sách bài tập toán 8 – Cánh diều
Tìm khẳng định sai: a) Nếu \(\Delta A'B'C'\backsim \Delta ABC\) thì \(\Delta ABC\backsim \Delta A'B'C'\).