1. Định nghĩa đường thẳng vuông góc với mặt phẳng
Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a trong mặt phẳng (P), kí hiệu \(d \bot (P)\) hoặc \((P) \bot d\).
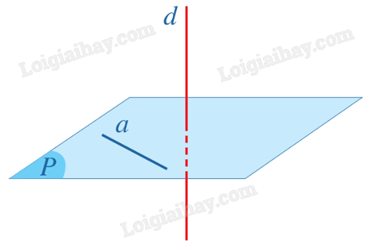
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
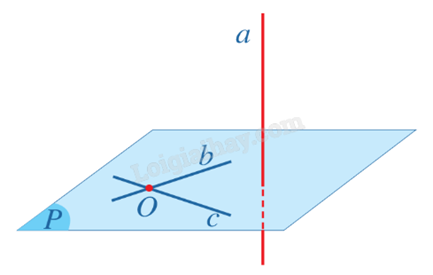
Ví dụ minh hoạ:
Cho hình chóp S.ABC có \(SA \bot AB\), \(SA \bot AC\). Chứng minh rằng \(SA \bot (ABC)\) và \(SA \bot BC\).
Giải:
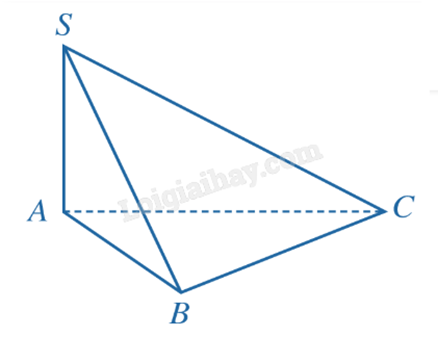
Ta có AB và AC là hai đường thẳng cắt nhau trong mặt phẳng (ABC) và \(SA \bot AB\), \(SA \bot AC\).
Suy ra \(SA \bot (ABC)\).
Mà \(BC \subset (ABC)\) nên \(SA \bot BC\).
3. Tính chất của đường thẳng vuông góc với mặt phẳng
Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Ví dụ minh hoạ:
1) Cho mặt phẳng (P) và đường thẳng a cắt (P) tại O sao cho \(a \bot (P)\). Giả sử b là đường thẳng đi qua điểm O và \(b \bot a\). Chứng minh rằng \(b \subset (P)\).
Giải:
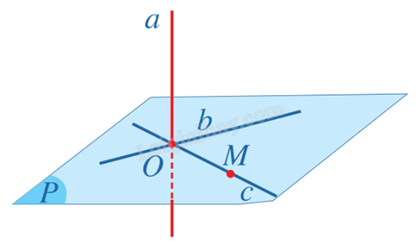
Ta lấy điểm M trong mặt phẳng (P), M khác O.
Nếu \(M \in b\) thì \(b \subset (P)\). Xét \(M \notin b\). Gọi c là đường thẳng đi qua O, M và (Q) là mặt phẳng đi qua b, c. Do \(a \bot b\), \(a \bot c\) nên \(a \bot (Q)\). Qua điểm O có hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a, suy ra hai mặt phẳng đó trùng nhau theo Tính chất 1. Vậy \(b \subset (P)\).
2) Cho mặt phẳng (P) và ba điểm A, B, C thoả mãn \((P) \bot AB\) và \((P) \bot {\rm{BC}}\). Chứng minh rằng \((P) \bot AC\).
Giải:
Vì hai đường thẳng AB và BC cùng đi qua điểm B và vuông góc với mặt phẳng (P) nên hai đường thẳng này trùng nhau. Suy ra A, B, C là ba điểm thẳng hàng và \((P) \bot AC\).

 Đường thẳng vuông góc với mặt phẳng - Từ điển môn Toán 11
Đường thẳng vuông góc với mặt phẳng - Từ điển môn Toán 11 






Danh sách bình luận