1. Khái niệm hàm số y = ax²
Hàm số y = ax2, là một dạng của hàm số bậc hai, là hàm số có dạng như sau: \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Khái niệm đồ thị của hàm số y = ax² (a ≠ 0)
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc toạ độ và có dạng như sau:
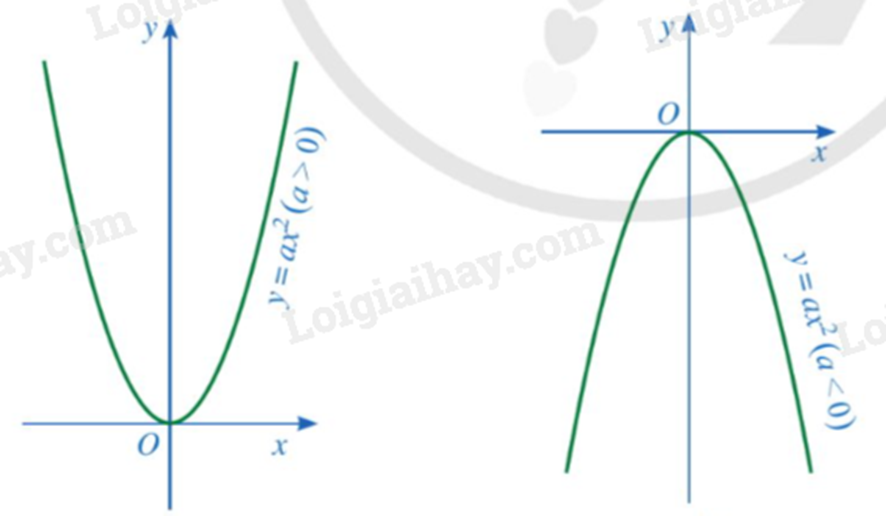
3. Cách vẽ đồ thị hàm số y = ax² (a ≠ 0)
- Lập bảng ghi một số cặp giá trị tương ứng của x và y.
Để lập bảng giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta tính các giá trị tương ứng của hàm số tại các điểm bất kỳ.
- Trong mặt phẳng toạ độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
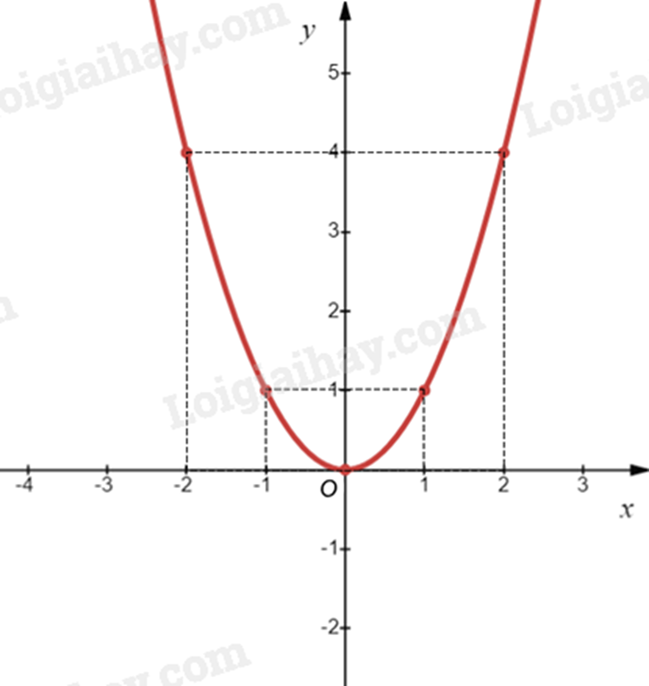
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).
Lập bảng một số giá trị tương ứng giữa x và y:

Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng toạ độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
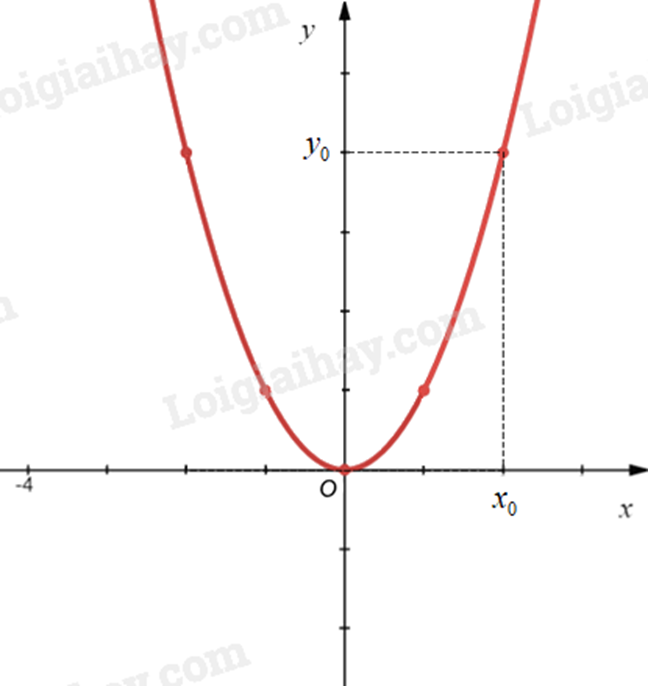
4. Các xác định toạ độ của một điểm thuộc đồ thị hàm số y = ax² (a ≠ 0)
+) Để xác định toạ độ của một điểm thuộc đồ thị hàm số y = ax² (a ≠ 0), ta thay giá trị \({x_0}\) vào hàm số hàm số y = ax² để được giá trị \({y_0}\) tương ứng.
+) Trên mặt phẳng toạ độ Oxy, ta có thể dựa vào toạ độ của điểm thuộc đồ thị hàm số để xác định hoành độ và tung độ của điểm đó.

 Hàm số y = ax² (a ≠ 0) - Từ điển môn Toán 9
Hàm số y = ax² (a ≠ 0) - Từ điển môn Toán 9 






Danh sách bình luận