1. Khái niệm hàm số y = ax²
Hàm số y = ax2, là một dạng của hàm số bậc hai, là hàm số có dạng như sau: \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Khái niệm đồ thị của hàm số y = ax² (a ≠ 0)
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc toạ độ và có dạng như sau:
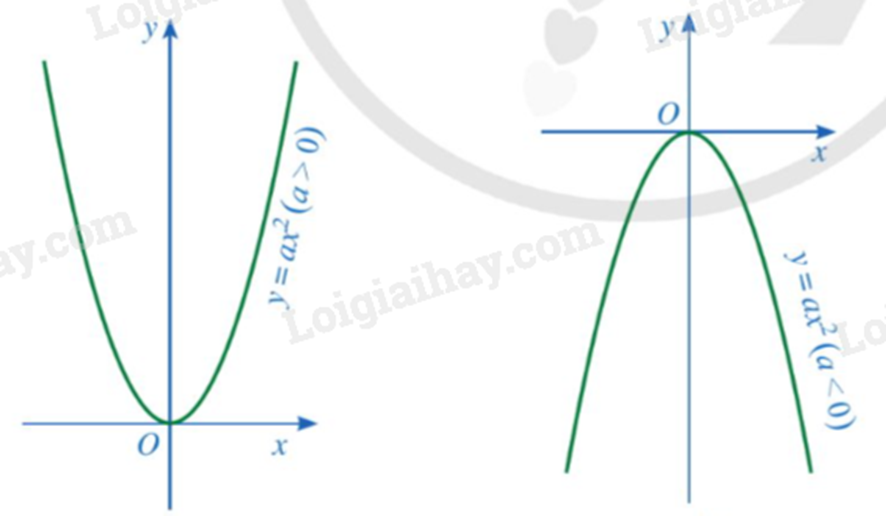
3. Tính chất của đồ thị hàm số y = ax² (a ≠ 0)
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong, gọi là đường parabol, có các tính chất sau:
- Có đỉnh là gốc toạ độ O;
- Có trục đối xứng là Oy;
- Nằm phía trên trục hoành nếu a > 0 và nằm phía dưới trục hoành nếu a < 0.
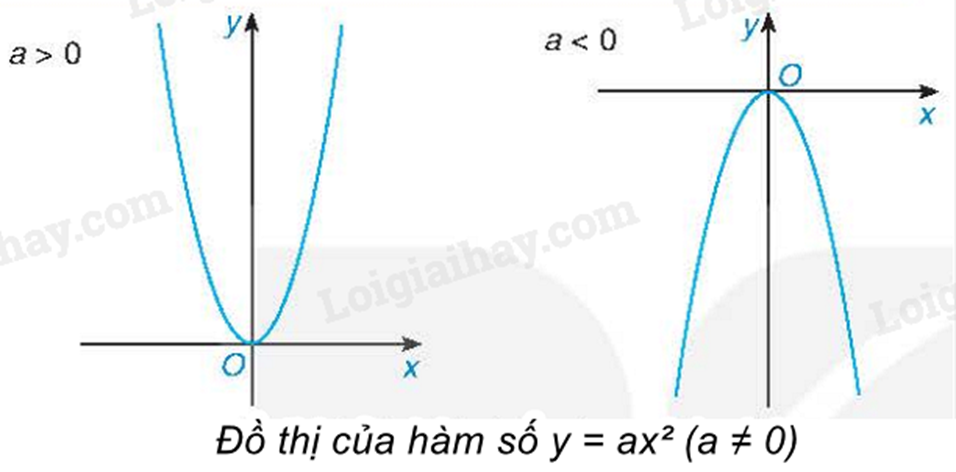
Nhận xét: Khi vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta cần xác định tối thiểu 5 điểm thuộc đồ thị là gốc toạ độ O và hai cặp điểm đối xứng với nhau qua trục tung Oy.
4. Đỉnh của đồ thị hàm số y = ax² (a ≠ 0)
Đỉnh của đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) chính là gốc toạ độ O.

 Hàm số y = ax² (a ≠ 0) - Từ điển môn Toán 9
Hàm số y = ax² (a ≠ 0) - Từ điển môn Toán 9 






Danh sách bình luận