Đề thi vào 10 môn Toán Thái Nguyên năm 2021
Tải vềCâu 1. Cho hàm số bậc nhất
Đề bài
Câu 1. Cho hàm số bậc nhất \(y = 2021x + 2022\). Hàm số đã cho là đồng biến hay nghịch biến trên \(\mathbb{R}\)? Vì sao?
Câu 2. Không dùng máy tính cầm tay, giải phương trình \(3{x^2} - 4x + 1 = 0\).
Câu 3. Rút gọn biểu thức \(A = \sqrt {20} - 2 - \sqrt {{{(\sqrt 5 - 2)}^2}} \).
Câu 4. Không dùng máy tính cầm tay, giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = - 3}\\{x + 3y = - 4}\end{array}} \right.\).
Câu 5. Cho biểu thức \(B = \dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}\), với \(x > 0\).
a) Rút gọn biểu thức \(B\).
b) Tìm giá trị của \(x\) để \(B = - 2\).
Câu 6. Một nhóm học sinh dự đinh làm 360 chiếc mũ chắn giọt bắn trong một thời gian nhất định để ủng hộ các địa phương trong công tác phòng, chống dịch bệnh COVID-19. Thựe tế, mỗi ngày nhóm học sinh làm vượt mức 12 chiếc mũ so với dự định. Vì vậy, nhóm đã làm xong trước thời gian dự định hai ngày và làm thêm đưọc 4 chiếc mũ. Hỏi theo dự định, mỗi ngày nhóm học sinh làm được bao nhiêu chiếc mũ ?
Câu 7. Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(BC = 10{\rm{cm}}\) và \(\sin \widehat {ACB} = \dfrac{3}{5}\). Tính độ dài các đoạn thẳng \(AB,AC\) và \(AH\).
Câu 8. Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(M(1;2)\). Xác định vị trí tương đối của đường tròn \((M;1)\) và các trục toạ độ.
Câu 9. Cho đường tròn \((O)\) và dây cung \(MN\) (MN không phải là đường kinh). Lấy điểm \(K\) thuộc đoạn thẳng \(MN\) sao cho \(KM > KN(K \ne N)\). Gọi \(I\) là điểm chính giữa của cung nhỏ \(MN\). Đường thẳng \(IK\) cắt đường tròn \((O)\) tại điểm \(E(E \ne I)\). Tiếp tuyến với đường tròn \((O)\) tại điểm \(E\) cắt đường thẳng \(MN\) tại điểm \(F\).
a) Chứng minh \(\widehat {NKE} = \widehat {IME}\);
b) Gọi \(P\) là điểm đối xứng với điểm \(K\) qua \(F\). Đường thẳng \(PE\) cắt đường tròn \((O)\) tại điểm \(Q(Q \ne E)\). Chứng minh \(IQ\) là đường kính của đường tròn \((O)\).
Câu 10. Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \((O)\) \((AB < AC)\). \(D\) là điểm nằm trên cung nhỏ \(BC(D \ne B,DB < DC)\). Lấy điểm \(E\) thuộc đoạn thẳng \(AD\) sao cho \(AE > ED(E \ne D)\). Đường trờn đường kinh \(ED\) cắt đường tròn \((O)\) tại điểm \(F(F \ne D,F \ne B,F \ne C)\). Đường thẳng \(DO\) và \(AF\) cắt đường tròn đường kính \(ED\) lần lượt tại các điểm \(M,N(M \ne D,N \ne F)\). Kẻ đường kính \(DK\) của đường tròn \((O)\). Chứng minh:
a) Bốn điểm \(A,E,M,K\) cùng thuộc một đường tròn;
b) Chứng minh: \(\Delta NAD = \Delta MAD\).
Lời giải chi tiết
Câu 1
Phương pháp:
Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R}\) khi \(a > 0\)
Cách giải:
Cho hàm số bậc nhất \(y = 2021x + 2022.\) Hàm số đã cho đồng biến hay nghịch biến trên \(\mathbb{R}\)? Vì sao?
Hàm số \(y = 2021x + 2022\) có \(a = 2021 > 0\) nên hàm số \(y = 2021x + 2022\) đồng biến trên \(\mathbb{R}\).
Câu 2
Phương pháp:
Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a}\)
Cách giải:
Không dùng máy tính cầm tay, giải phương trình \(3{x^2} - 4x + 1 = 0.\)
Phương trình \(3{x^2} - 4x + 1 = 0\) có \(a + b + c = 3 - 4 + 1 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = 1\) và \({x_2} = \dfrac{c}{a} = \dfrac{1}{3}\).
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ {\dfrac{1}{3};1} \right\}\).
Câu 3
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
Rút gọn biểu thức \(A = \sqrt {20} - 2 - \sqrt {{{(\sqrt 5 - 2)}^2}} \)
Ta có:
\(\begin{array}{*{20}{l}}A&{ = \sqrt {20} - 2 - \sqrt {{{(\sqrt 5 - 2)}^2}} }\\{}&{ = \sqrt {4.5} - 2 - |\sqrt 5 - 2|}\\{}&{ = 2\sqrt 5 - 2 - \sqrt 5 + 2({\rm{ do }}\sqrt 5 - 2 > 0)}\\{}&{ = \sqrt 5 }\end{array}\)
Vậy \(A = \sqrt 5 \).
Câu 4
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(y\)
Sử dụng phương pháp thế, tìm được nghiệm \(x\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
Không dùng máy tính cầm tay, giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = - 3}\\{x + 3y = - 4}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{x + 2y = - 3}\\{x + 3y = - 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = - 1}\\{x = - 2y - 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 2.( - 1) - 3}\\{y = - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = - 1}\\{x = - 1}\end{array}} \right.} \right.} \right.} \right.\)
Vậy hệ phương trình có tập nghiệm \(S = \{ ( - 1; - 1)\} \).
Câu 5
Phương pháp:
a) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
b) Giải phương trình: \(B = - 2\)
Đối chiếu điều kiện và kết luận.
Cách giải:
Cho biểu thức \(B = \dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}\) với \(x > 0\)
a) Rút gọn biểu thức \(B\);
ĐKXĐ: \(x > 0\)
\(B = \dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}\)
\( = \dfrac{{x - 6}}{{\sqrt x (\sqrt x + 3)}} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}\)
\( = \dfrac{{x - 6 - (\sqrt x + 3) + \sqrt x }}{{\sqrt x (\sqrt x + 3)}}\)
\( = \dfrac{{x - 6 - \sqrt x - 3 + \sqrt x }}{{\sqrt x (\sqrt x + 3)}}\)
\( = \dfrac{{x - 9}}{{\sqrt x (\sqrt x + 3)}}\)
\( = \dfrac{{(\sqrt x + 3)(\sqrt x - 3)}}{{\sqrt x (\sqrt x + 3)}}\)
\( = \dfrac{{\sqrt x - 3}}{{\sqrt x }}\)
Vậy \(B = \dfrac{{\sqrt x - 3}}{{\sqrt x }}\).
b) Tìm giá trị của \(x\) để \(B = - 2\)
Điều kiện: \(x > 0\).
Ta có: \(B = - 2\)
\( \Leftrightarrow \dfrac{{\sqrt x - 3}}{{\sqrt x }} = - 2\)
\( \Rightarrow \sqrt x - 3 = - 2\sqrt x \)
\( \Leftrightarrow 3\sqrt x = 3\)
\( \Leftrightarrow \sqrt x = 1\)
\( \Leftrightarrow x = 1(\) TMDK \()\)
Vậy \(x = 1\) thì \(B = - 2.\)
Câu 6
Phương pháp:
Gọi số chiếc mũ mỗi ngày nhóm học sinh dự định là được là \(x\) (chiếc), \(\left( {x \in {\mathbb{N}^*},x < 360} \right)\).
Tính được thời gian dự định nhóm học sinh làm xong
Tính được số chiếc mũ, thời gian thực tế học sinh làm xong
Từ giả thiết, lập được phương trình, giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Một nhóm học sinh dự định làm 360 chiếc mũ chắn giọt bán trong một thời gian nhất định để ủng hộ các dịa phuơng trong công tác phòng, chống dịch COVID-19. Thục tế, mỗi ngày nhóm học sinh làm vuợt mức 12 chiếc mũ so với dự dịnh. Vì vậy, nhóm đã làm xong trước thời gian dự định hai ngày và làm thêm được 4 chiếc mũ. Hỏi theo dự định, mỗi ngày nhóm học sinh làm được bao nhiêu chiếc mũ?
Gọi số chiếc mũ mỗi ngày nhóm học sinh dự định là được là \(x\) (chiếc), \(\left( {x \in {\mathbb{N}^*},x < 360} \right)\).
\( \Rightarrow \) Thời gian dự định nhóm học sinh làm xong 360 chiếc mũ là: \(\dfrac{{360}}{x}\) (ngày)
Thực tế mỗi ngày, nhóm học sinh làm được số chiếc mũ là: \(x + 12\) (chiếc).
\( \Rightarrow \) Thời gian thực tế nhóm học sinh hoàn thành \(360 + 4 = 364\) chiếc mũ là: \(\dfrac{{364}}{{x + 12}}\) (ngày)
Nhóm học sinh đã hoàn thành xong trước dự định 2 ngày nên ta có phương trình:
\(\begin{array}{l}\dfrac{{360}}{x} - \dfrac{{364}}{{x + 12}} = 2\\ \Leftrightarrow 360(x + 12) - 364x = 2x(x + 12)\\ \Leftrightarrow 2{x^2} + 24x = 360x + 4320 - 364x\\ \Leftrightarrow 2{x^2} + 28x - 4320 = 0\\ \Leftrightarrow {x^2} + 14x - 2160 = 0\end{array}\)
Phương trình có: \(\Delta ' = {( - 7)^2} + 1.2160 = 2209 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = - 7 + \sqrt {2209} = 40(tm)\) và \({x_2} = - 7 - \sqrt {2209} = - 54(ktm)\)
Vậy theo dự định, mỗi ngày nhóm học sinh làm được 40 chiếc mũ.
Câu 7
Phương pháp:
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông
Áp dụng hệ thức lượng trong tam giác vuông
Áp dụng định lý Py – ta – go
Cách giải:
Cho tam giác \(ABC\) vuông tại \(A\), dường cao \(AH\). Biết \(BC = 10{\rm{cm}}\) và \(\sin \widehat {ACB} = \dfrac{3}{5}.\) Tính độ dài các dọn thẳng \(AB,AC\) và \(AH.\)

Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(\sin \widehat {ACB} = \dfrac{{AB}}{{BC}} \Rightarrow AB = BC \cdot \sin \widehat {ACB} = 10 \cdot \dfrac{3}{5} = 6({\rm{cm}}).\)
Áp dụng định lí Py – ta – go cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,A{B^2} + A{C^2} = B{C^2}\\ \Rightarrow A{C^2} = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8({\rm{cm}}).\end{array}\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)
\( \Rightarrow AH = \dfrac{{AB \cdot AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8({\rm{cm}})\)
Vậy \(AB = 6{\rm{cm}},AC = 8{\rm{cm}},AH = 4,8{\rm{cm}}\)
Câu 8
Phương pháp:
Gọi \(R\) là bán kính đường tròn \((M;1) \Rightarrow R = 1\).
Gọi \(A,B\) lần lượt là hình chiếu vuông góc của \(M\) lên các trục tọa độ \(Ox,Oy\).
Tính độ dài \(MA,MB\) so sánh với \(R\) và kết luận.
Cách giải:
Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(M(1;2).\) Xác định vị trí tương đối của đường tròn \((M;1)\) và các trục tọa độ.
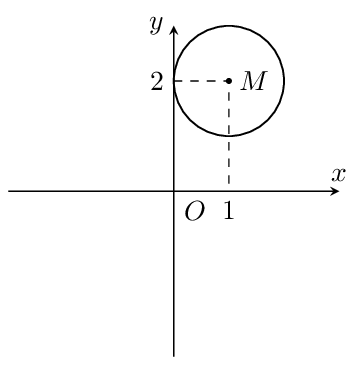
Gọi \(R\) là bán kính đường tròn \((M;1) \Rightarrow R = 1\).
Gọi \(A,B\) lần lượt là hình chiếu vuông góc của \(M\) lên các trục tọa độ \(Ox,Oy\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BM \bot OB}\\{MA \bot OA \Rightarrow OAMB{\rm{ }}}\\{OA \bot OB}\end{array}} \right.\)là hình chữ nhật
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{MB = OA = 1 = R}\\{MA = BO = 2 > R}\end{array}} \right.\)
\( \Rightarrow Oy\) tiếp xúc với \((M;1)\) tại \(B\) và \(Ox\) không cắt đường tròn \((M;1)\).
Câu 9
Phương pháp:
a) Ta sẽ chứng minh: \(\widehat {IEM} = \widehat {INM}\) và \(\widehat {IMN} = \widehat {INM}\), từ đó suy ra \(\widehat {NKE} = \widehat {IME}\)
b) Ta sẽ chứng minh: \(\widehat {IEQ} = 90^\circ \) nên là góc nội tiếp chắn nửa đường tròn do đó, \(IQ\) là đường kính của đường tròn \((O)\)
Cách giải:
Cho đường tròn \((O)\) và dây cung \(MN\) (\(MN\) không phải là đường kính). Lấy điểm \(K\) thuộc đoạn thẳng \(MN\) sao cho \(KM > KN(K \ne N).\) Goi \(I\) là điểm chính giữa của cung nhỏ \(MN\). Đường thẳng \(IK\) cắt đường tròn \((O)\) tại điểm \(E(E \ne I).\) Tiếp tuyến với đường tròn \((O)\) tại điểm \(E\) cắt đường thẳng \(MN\) tại \(F.\)

a) Chứng minh \(\widehat {NKE} = \widehat {IME}\).
Ta có: \(\widehat {NKE} = \widehat {IEM} + \widehat {EMN}\) (tính chất góc ngoài tam giác \(EMK\)).
\(\widehat {IME} = \widehat {IMN} + \widehat {EMN}\)
Ta có \(\widehat {IEM} = \widehat {INM}\) ( 2 góc nội tiếp cùng chắn cung \(MI\)).
Lai có \(I\) là điểm chính giữa cung \(MN\) suy ra \(IM = IN\) (hai cung bằng nhau căng 2 dây bằng nhau).
\( \Rightarrow \Delta IMN\) là tam giác cân tại \(I\)
\( \Rightarrow \widehat {IMN} = \widehat {INM}\) (tính chất tam giác cân).
Suy ra \(\widehat {NKE} = \widehat {IME}\).
b) Gọi \(P\) là điểm đối xứng với diểm \(K\) qua \(F\). Đường thẳng \(PE\) cắt đường tròn \((O)\) tại điểm \(Q(Q \ne E)\)
Chứng minh \(IQ\) là đường kính của đường tròn \((O)\).
Ta có: \(\widehat {FKE} = \widehat {IEM} + \widehat {NME}\) (tính chất góc ngoài tam giác)
\(\widehat {FEK} = \widehat {NEI} + \widehat {FEN}\)
Mà: \(\widehat {FEN} = \widehat {NME}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(NE\) ).
Trong \((O)\) có: \(\widehat {IEM} = \widehat {IEN}\) (hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra \(\widehat {FEK} = \widehat {FKE}\).
Suy ra tam giác \(FEK\) cân tại \(F\) suy ra \(FE = FK\) (tính chất tam giác cân).
Mặt khác \(FK = FP\) (gt) nên \(FE = FK = FP = \dfrac{1}{2}PK\).
Tam giác \(EKP\) có \(FE = FK = FP = \dfrac{1}{2}PK\) suy ra tam giác \(EKP\) vuông tại \(E\).
Suy ra \(EK \bot EP\) hay \(EI \bot PQ\), suy ra \(\widehat {IEQ} = 90^\circ \) nên là góc nội tiếp chắn nửa đường tròn.
Vậy \(IQ\) là đường kính của đường tròn \((O)\) (đpcm).
Câu 10
Phương pháp:
a) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp, chứng minh \(AEMK\) nội tiếp đường tròn (tứ giác có tổng hai góc dối bằng \(180^\circ \)), do đó điểm \(A,E,M,K\) cùng thuộc một đường tròn
b) + \(E\), \(F\), \(K\) thẳng hàng.
+ \(\Delta EDN = \Delta EDM\) (cạnh huyền – góc nhọn) \( \Rightarrow ND = MD(2\) cạnh tương ứng).
+ \(\Delta NDA = \Delta MDA\) (cạnh - góc - cạnh).
Cách giải:
Cho tam giác \(ABC\) nhọn nội tiếp dường tròn \((O)\) (AB \( < AC).\) \(D\) là điểm nằm trên cung nhỏ \(BC\) \((D \ne B,DB\) \( < DC).\) Lấy điểm \(E\) thuộc đoạn thẳng \(AD\) sao cho \(AE > ED(E \ne D).\) Đường tròn đường kính \(ED\) cắt đường tròn \((O)\) tại điểm \(F(F \ne D,F \ne B,F \ne C).\) Đường thẳng \(DO\) và \(AF\) cắt đường tròn đường kính \(ED\) lần lượt tại các điểm \(M,N(M \ne D,N \ne F).\) Kẻ đường kinh \(DK\) của đường tròn \((O)\). Chứng minh:

a) Ta có \(\widehat {DME} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn đường kính \(DE)\)
\( \Rightarrow EM \bot DK \Rightarrow \widehat {EMK} = 90^\circ \) và \(\widehat {DAK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left. {(O)} \right)\).
\( \Rightarrow \widehat {EAK} = 90^\circ \)
Xét tứ giác \(AEMK\) có: \(\widehat {EAK} + \widehat {EMK} = 90^\circ + 90^\circ = 180^\circ \)
\( \Rightarrow \) tứ giác \(AEMK\) nội tiếp đường tròn (tứ giác có tổng hai góc dối bằng \(180^\circ \) ).
Vậy bốn điểm \(A,E,M,K\) cùng thuộc một đường tròn.
b) Ta có \(\widehat {EFD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn đường kính \(ED\) ) \( \Rightarrow EF \bot FD\) (1)
Tương tự \(\widehat {DFK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left. {(O)} \right)\) \( \Rightarrow KF \bot FD\) (2)
Từ (1) và (2) suy ra \(E\), \(F\), \(K\) thẳng hàng.
Xét đường tròn đường kính \(ED\), ta có \(\widehat {NFE} = \widehat {NDE}(2\) góc nội tiếp cùng chắn \(\widehat {NE}\) ) hay \(\widehat {AFK} = \) \(\widehat {NDE}\)
Lại có \(\widehat {AFK} = \widehat {ADK}(2\) góc nội tiếp cùng chắn \(\widehat {AK}\) ) hay \(\widehat {AFK} = \widehat {EDM}\). Từ (3) và (4) suy ra \(\widehat {NDE} = \widehat {EDM}\) (cùng bằng \(\widehat {AFK}\) ).
Xét \(\Delta EDN\) và \(\Delta EDM\) có:
\(\widehat {END} = \widehat {EMD} = 90^\circ \)
\(ED\) : cạnh chung.
\(\widehat {NDE} = \widehat {EDM}\) (chứng minh trên).
\( \Rightarrow \Delta EDN = \Delta EDM\) (cạnh huyền - góc nhọn)
\( \Rightarrow ND = MD(2\) cạnh tương ứng).
Xét \(\Delta NAD\) và \(\Delta MAD\) có
\(ND = MD.\)
\(AD:\) cạnh chung.
\(\widehat {NDA} = \widehat {MDA}\) (chứng minh trên).
\( \Rightarrow \Delta NDA = \Delta MDA\) (cạnh - góc - cạnh).













Danh sách bình luận