Đề thi vào 10 môn Toán Quảng Trị năm 2023
Tải vềCâu 1: Xét hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau. Khẳng định nào dưới đây đúng? A. Cung lớn hơn căng dây nhỏ hơn.
Đề bài
Câu 1: Xét hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau. Khẳng định nào dưới đây đúng?
A. Cung lớn hơn căng dây nhỏ hơn.
B. Cung lớn hơn căng dây lớn hơn.
C. Dây lớn hơn căng cung nhỏ hơn.
D. Cung nhỏ hơn căng dây lớn hơn.
Câu 2: Trong các khằng định sau, khẳng định nào đúng?
A. Góc có đỉnh nằm bên trong đường tròn được gọi là góc ở tâm.
B. Góc có đỉnh nằm trên đường tròn được gọi là góc ở tâm.
C. Góc có đỉnh nằm bên ngoài đường tròn được gọi là góc ở tâm.
D. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Câu 3: Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) thì \({x_1} + {x_2}\) bằng
A. \( - \frac{c}{a}\).
B. \( - \frac{b}{a}\).
C. \(\frac{b}{a}\).
D. \(\frac{c}{a}\).
Câu 4: Cho tam giác ABC vuông tại \(A\) và có đường cao AH. Khẳng định nào dưới đây đúng?
A. \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2} + A{C^2}}}\).
B. \(\frac{1}{{A{H^2}}} = A{B^2} + A{C^2}\).
C. \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} - \frac{1}{{A{C^2}}}\).
D. \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).
Câu 5: Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}\)?
A. \(y = 3{x^2}\).
B. \(y = {\rm{ \;}} - 2x + 1\).
C. \(y = 3x - 5\).
D. \(y = {\rm{ \;}} - x + 1\).
Câu 6: Cho góc BIC có đỉnh \(I\) nằm bên trong đường tròn \((O)\). Hai cung bị chắn của góc BIC là \(\widehat {BnC}\) và \(\widehat {AmD}\) (hình vẽ).
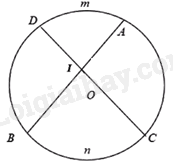
Số đo cùa \(\widehat {BIC}\) được tính theo công thức nào dưới đây?
A. \(\angle BIC = \frac{1}{2}sdc{\mkern 1mu} BnC\).
B. \(\angle BIC = \frac{1}{2}(sdcBnC + sdcAmD)\)
C. \(\widehat {BIC} = \frac{1}{2}(sdcBnC - sdcAmD)\).
D. \(\angle BIC = \frac{1}{2}\;{\rm{sd}}cAmD\).
Câu 7: Hệ số góc của đường thẳng \(y = {\rm{ \;}} - \frac{3}{4}x - 2023\) bằng
A. -2023 .
B. 2023 .
C. \( - \frac{3}{4}\).
D. \(\frac{3}{4}\).
Câu 8: Trong các khẳng định sau, khẳng định nào đúng?
A. \(\cos 60^\circ = \tan 30^\circ \).
B. \(\cos 60^\circ = \cot 30^\circ \).
C. \(\cos 60^\circ = \cos 30^\circ \).
D. \(\cos 60^\circ = \sin 30^\circ \).
Câu 9: Phương trình nào dưới đây là phương trình bậc nhất theo hai ẩn \(x\) và \(y\) ?
A. \({x^2} - 4y = 1\).
B. \(4x + 3{y^2} = 2\).
C. \({x^2} + {y^2} = 10\).
D. \(3x - y = 5\).
Câu 10: Cặp số \((x;y)\) nào dưới đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + 3y = 5}\\{x - 2y = {\rm{ \;}} - 1}\end{array}} \right.\) ?
A. \((x;y) = ( - 1;1)\).
B. \((x;y) = (1;1)\).
C. \((x;y) = ( - 1; - 1)\).
D. \((x;y) = (1; - 1)\).
Câu 11: Trong một đường tròn. Khẳng định nào dưới đây sai?
A. Đường kính đi qua trung điểm của một đây không đi qua tâm thì vuông góc với dây ấy.
B. Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
C. Đường kính là dây lớn nhất.
D. Đường kính đi qua trung điểm của một dây thì vuông góc với dây ấy.
Câu 12: Cho hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\). Khẳng định nào đưới đây đúng?
A. Hàm số nghịch biến khi \(x < 0\).
B. Hàm số đồng biến khi \(x > 0\).
C. Hàm số nghịch biến trên \(\mathbb{R}\).
D. Hàm số đồng biến khi \(x < 0\).
Câu 13: Bằng các phép biến đổi đại số, rút gọn các biểu thức sau:
a) \(A = \sqrt 8 {\rm{ \;}} - \sqrt 2 \)
b) \(B = \frac{{a + 2\sqrt a }}{{\sqrt a {\rm{ \;}} + 2}}\)
Câu 14: a) Vẽ đồ thị hàm số \(y = 2{x^2}\).
b) Không dùng máy tính cầm tay, giải phương trình \({x^2} - 5x + 6 = 0\)
Câu 15: Một xe khách và một xe tải xuất phát cùng một thời điểm từ A đến B. Do vận tốc xe khách lớn hơn vận tốc xe tải \(10km/h\) nên xe khách đến sớm hơn xe tải 36 phút. Tính vận tốc của mỗi xe, biết quãng đường từ A đến B dài \(180\;{\rm{km}}\).
Câu 16:
Cho phương trình \({x^2} - 3\left( {m + 2} \right)x + {m^2} + 7m = 0\) (1) (với x là ẩn, m là tham số)
a) Tìm tất cả các giá trị nguyên của m để phương trình (1) có hai nghiệm trái dấu
b) Tìm tất cả các giá trị thực của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\) và \(3{x_1} - 3x_2^2 + (9m + 20){x_2} - 3{m^2} - 21m - 19 = 0\)
Câu 17: Cho tam giác ABC nhọn, nội tiếp đường tròn (O) và có đường cao AH. Kẻ \(HD \bot AB{\mkern 1mu} \)và \(HE \bot AC{\mkern 1mu} \)\({\mkern 1mu} \left( {D \in AB,{\mkern 1mu} {\mkern 1mu} E \in AC} \right)\)
a) Chứng minh tứ giác ADHE nội tiếp.
b) Tính số đo \(\angle EDB\), biết \(\angle ACB = 40^\circ \)
c) Đường thẳng qua E và vuông góc với AB cắt tia AO tại M. Chứng minh \(DM \bot AE.{\mkern 1mu} \)
----- HẾT -----
Lời giải chi tiết
|
1.B |
2.D |
3.B |
4.D |
5.C |
6.B |
|
7.C |
8.D |
9.D |
10.B |
11.D |
12.D |
Câu 1 (NB):
Phương pháp:
Lý thuyết về quan hệ hai dây cung trong đường tròn.
Cách giải:
Cung lớn hơn căng dây lớn hơn.
Chọn B.
Câu 2 (NB):
Phương pháp:
Lý thuyết góc ở tâm, góc nội tiếp.
Cách giải:
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Chọn D.
Câu 3 (NB):
Phương pháp:
Hệ thức Viet
Cách giải:
\(a{x^2} + bx + c = 0\) có nghiệm \({x_1},{x_2} \Rightarrow {x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}\)
Chọn B.
Câu 4 (NB):
Phương pháp:
Hệ thức lượng trong tam giác vuông
Cách giải:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
Chọn D.
Câu 5 (NB):
Phương pháp:
Hàm số bậc nhất \(y = ax + b\) đồng biến khi \(a > 0\)
Cách giải:
Hàm số bậc nhất \(y = ax + b\) đồng biến khi \(a > 0\) nên \(y = 3x - 5\) đồng biến trên \(\mathbb{R}\).
Chọn C.
Câu 6 (NB):
Phương pháp:
Công thức góc có đỉnh bên trong đường tròn
Chú ý khi giải:
\(\angle BIC = \frac{1}{2}(sdcBnC + sdcAmD)\)
Chọn B.
Câu 7 (NB):
Phương pháp:
Đường thẳng \(y = ax + b\) có hệ số góc \(k = a\)
Cách giải:
Hệ số góc của đường thẳng \(y = {\rm{ \;}} - \frac{3}{4}x - 2023\) bằng \( - \frac{3}{4}\)
Chọn C.
Câu 8 (NB):
Phương pháp:
Tính chất hai góc phụ nhau
Cách giải:
Hai góc phụ nhau thì chéo nhau nên \(\cos 60^\circ = \sin 30^\circ \)
Chọn D.
Câu 9 (NB):
Phương pháp:
Phương trình bậc nhất 2 ẩn có dạng \(ax + by = c\)
Cách giải:
\(3x - y = 5\) là phương trình nào dưới đây là phương trình bậc nhất theo hai ẩn \(x\) và \(y\).
Chọn D.
Câu 10 (NB):
Phương pháp:
Giải hệ bằng phương pháp thế hoặc cộng đại số hoặc bằng casio
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{2x + 3y = 5}\\{x - 2y = {\rm{ \;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + 3y = 5}\\{2x - 4y = {\rm{ \;}} - 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{7y = 7}\\{x = 2y - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 1}\\{x = 1}\end{array}} \right.\)
Chọn B.
Câu 11 (NB):
Phương pháp:
Quan hệ đường kính và dây cung
Cách giải:
Đường kính đi qua trung điểm của một dây thì vuông góc với dây ấy là sai vì dây đó phải không đi qua tâm đường tròn.
Chọn D.
Câu 12 (NB):
Phương pháp:
Hàm số \(y = a{x^2}\) có \(a < 0\) đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\)
Cách giải:
Hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\) có \(a < 0\) đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\)
Chọn D.
Câu 13 (TH):
Cách giải:
a, \(A = \sqrt 8 {\rm{\;}} - \sqrt 2 \)
Ta có: \(A = \sqrt 8 {\rm{\;}} - \sqrt 2 {\rm{\;}} = \sqrt {{2^2}.2} {\rm{\;}} - \sqrt 2 \) \( = 2.\sqrt 2 {\rm{\;}} - \sqrt 2 {\rm{\;}} = \sqrt 2 \).
b, \(B = \frac{{a + 2\sqrt a }}{{\sqrt a {\rm{\;}} + 2}}\)
Ta có: \(B = \frac{{a + 2\sqrt a }}{{\sqrt a {\rm{\;}} + 2}}\) (Điều kiện: \(a \ge 0\))
\( = \frac{{\sqrt a \left( {\sqrt a {\rm{\;}} + 2} \right)}}{{\sqrt a {\rm{\;}} + 2}} = \sqrt a \)
Vậy \(B = \sqrt a \) với \(a \ge 0\)
Câu 14 (TH):
Phương pháp:
a) Lập bảng giá trị x, y và vẽ đồ thị, kết luận
b) Dùng phương pháp nhẩm nghiệm.
Cách giải:
a) Vẽ đồ thị hàm số \(y = 2{x^2}\).
Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O{\mkern 1mu} \left( {0;0} \right);A\left( { - 2;8} \right);{\mkern 1mu} {\mkern 1mu} B\left( { - 1;2} \right);C\left( {1;2} \right);{\mkern 1mu} {\mkern 1mu} D\left( {2;8} \right)\)
Hệ số \(a = 2 > 0\)nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
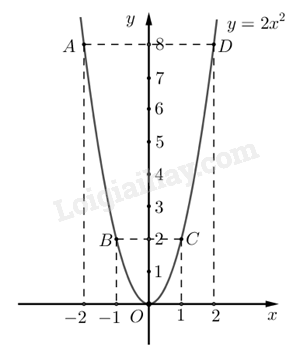
b) Không dùng máy tính cầm tay, giải phương trình \({x^2} - 5x + 6 = 0\)
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {x^2} - 5x + 6 = 0}\\{ \Leftrightarrow {x^2} - 2x - 3x + 6 = 0}\\{ \Leftrightarrow x\left( {x - 2} \right) - 3\left( {x - 2} \right) = 0}\\{ \Leftrightarrow \left( {x - 3} \right)\left( {x - 2} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 3 = 0}\\{x - 2 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = 2}\end{array}} \right.}\end{array}\)
Vậy phương trình là: \(S = \left\{ {2;3} \right\}\).
Câu 15 (TH):
Cách giải:
Gọi x (km/h) là vận tốc của xe tải.
Do vận tốc xe khách lớn hơn vận tốc xe tải \(10km/h\) nên xe khách có vận tốc là: \(x + 10{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right)\).
Thời gian đi của xe tải là: \(\frac{{180}}{x}\) (giờ).
Thời gian đi của xe khách là: \(\frac{{180}}{{x + 10}}\) (giờ).
Đổi 36 phút = 0,6 giờ.
Vì xe khách đến sớm hơn xe tải 36 phút nên ta có: \(\frac{{180}}{x} - \frac{{180}}{{x + 10}} = 0,6\)
\(\begin{array}{l} \Leftrightarrow \frac{{180\left( {x + 10} \right)}}{{x\left( {x + 10} \right)}} - \frac{{180x}}{{x\left( {x + 10} \right)}} = 0,6\\ \Leftrightarrow \frac{{180\left( {x + 10} \right) - 180x}}{{x\left( {x + 10} \right)}} = 0,6\\ \Leftrightarrow \frac{{180x + 1800 - 180x}}{{x\left( {x + 10} \right)}} = 0,6\\ \Leftrightarrow \frac{{1800}}{{{x^2} + 10x}} = 0,6\\ \Leftrightarrow 0,6\left( {{x^2} + 10x} \right) = 1800\\ \Leftrightarrow 0,6{x^2} + 6x - 1800 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 50\,\,\,\,\,\,\,\left( {tm} \right)}\\{x = - 60\,\,\,\,\,\,\left( {ktm} \right)}\end{array}} \right.\end{array}\)
Vậy vận tốc của xe tải là 50 km/h; vận tốc của xe khách là 60km/h.
Câu 16 (TH):
Phương pháp:
a) Phương trình có 2 nghiệm trái dấu khi \(ac < 0\)
b) Áp dụng hệ thức Viet
Cách giải:
a) Tìm tất cả các giá trị nguyên của m để phương trình (1) có hai nghiệm trái dấu
để phương trình có hai nghiệm trái dâu thì \(a.c < 0 \Leftrightarrow 1\left( {{m^2} + 7m} \right) < 0\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow m\left( {m + 7} \right) < 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{m > 0}\\{m + 7 < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{m < 0}\\{m + 7 > 0}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{m > 0}\\{m < {\rm{ \;}} - 7}\end{array}} \right.\left( {VL} \right)}\\{\left\{ {\begin{array}{*{20}{l}}{m < 0}\\{m > {\rm{ \;}} - 7}\end{array}} \right.}\end{array}} \right. \Leftrightarrow {\rm{ \;}} - 7 < m < 0}\end{array}\)
Vậy \( - 7 < m < 0\) thì phương trình (1) có 2 nghiệm trái dấu.
b) Tìm tất cả các giá trị thực của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\) và \(3{x_1} - 3x_2^2 + (9m + 20){x_2} - 3{m^2} - 21m - 19 = 0\)
Phương trình (1) có
\(\begin{array}{*{20}{l}}{\Delta {\rm{ \;}} = {{\left( { - 3\left( {m + 2} \right)} \right)}^2} - 4.1.\left( {{m^2} + 7m} \right)}\\{ = 9\left( {{m^2} + 4m + 4} \right) - 4{m^2} - 28m}\\{ = 5{m^2} + 8m + 36}\\{ = 5\left( {{m^2} + \frac{8}{5}m + \frac{{36}}{5}} \right)}\end{array}\)
\(\begin{array}{*{20}{l}}{ = 5\left( {{m^2} + \frac{8}{5}m + \frac{{16}}{{25}} + \frac{{164}}{{25}}} \right)}\\{ = 5{{\left( {m + \frac{4}{5}} \right)}^2} + \frac{{164}}{5}{\mkern 1mu} {\mkern 1mu} \forall m}\end{array}\)
Vậy phương trình (1) luôn có 2 nghiệm phân biệt với mọi m.
Giả sử 2 nghiệm đó là \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\)
Theo hệ thức Viet ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 3\left( {m + 2} \right)}\\{{x_1}{x_2} = {m^2} + 7m}\end{array}} \right.\) (2)
Do \({x_2}\) là nghiệm của (1) nên \({x_2}^2 - 3\left( {m + 2} \right){x_2} + {m^2} + 7m = 0\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 3\left( {{x_2}^2 - 3\left( {m + 2} \right){x_2} + {m^2} + 7m} \right) = 0}\\{ \Leftrightarrow 3{x_2}^2 - \left( {9m + 18} \right){x_2} + 3{m^2} + 21m = 0}\\{ \Leftrightarrow 3{x_2}^2 - \left( {9m + 20} \right){x_2} + 3{m^2} + 21m = {\rm{ \;}} - 2{x_2}}\end{array}\)
Để \(3{x_1} - 3x_2^2 + (9m + 20){x_2} - 3{m^2} - 21m - 19 = 0\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 3{x_1} - 19 = 3x_2^2 - (9m + 20){x_2} + 3{m^2} + 21m}\\{ \Leftrightarrow 3{x_1} - 19 = {\rm{ \;}} - 2{x_2}}\\{ \Leftrightarrow 3{x_1} + 2{x_2} = 19}\end{array}\)
Kết hợp với (2) ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 3\left( {m + 2} \right)}\\{3{x_1} + 2{x_2} = 19}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2{x_1} + 2{x_2} = 6\left( {m + 2} \right)}\\{3{x_1} + 2{x_2} = 19}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 3\left( {m + 2} \right) - {x_1}}\\{{x_1} = 7 - 6m}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = 7 - 6m}\\{{x_2} = 9m - 1}\end{array}} \right.\)
Thay \({x_1},{x_2}\) vào phương trình \({x_1}{x_2} = {m^2} + 7m\) ta được
\(\begin{array}{*{20}{l}}{\left( {7 - 6m} \right)\left( {9m - 1} \right) = {m^2} + 7m}\\{ \Leftrightarrow 63m - 7 - 54{m^2} + 6m = {m^2} + 7m}\\{ \Leftrightarrow 55{m^2} - 62m + 7 = 0}\\{ \Leftrightarrow \left( {m - 1} \right)\left( {55m - 7} \right) = 0}\end{array}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = \frac{7}{{55}}}\end{array}} \right.\) (thỏa mãn)
Vậy \(\left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = \frac{7}{{55}}}\end{array}} \right.\) thì phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\) và
\(3{x_1} - 3x_2^2 + (9m + 20){x_2} - 3{m^2} - 21m - 19 = 0\)
Câu 17 (VD):
Cách giải:
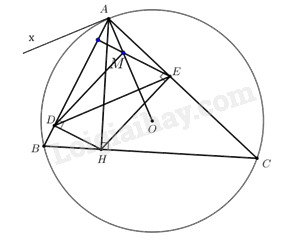
a) Chứng minh tứ giác ADHE nội tiếp.
Từ giả thiết ta có:
\(HD \bot AB{\mkern 1mu} \Rightarrow \angle ADH = 90^\circ \)(tính chất)
\(HE \bot AC{\mkern 1mu} \Rightarrow \angle AEH = 90^\circ \)(tính chất)
\( \Rightarrow \angle ADH + \angle AEH = 90^\circ + 90^\circ {\rm{\;}} = 180^\circ \)
Mà \(\angle ADH\) và \(\angle AEH\)ở vị trí đối nhau nên tứ giác ADHE nội tiếp (dhnb) (đpcm)
b) Tính số đo \(\angle EDB\), biết \(\angle ACB = 40^\circ \)
Ta có: \(HD \bot AB{\mkern 1mu} {\mkern 1mu} \left( {{\rm{gt}}} \right) \Rightarrow \angle BDH = 90^\circ \)(tính chất)
Tam giác AHC vuông tại H nên \(\angle ACH + \angle CAH = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau).
\( \Rightarrow \angle CAH = 90^\circ - \angle ACH = 90^\circ - 40^\circ {\rm{\;}} = 50^\circ \) hay \(\angle EAH = 50^\circ \)
Vì tứ giác ADHE nội tiếp (chứng minh câu a) nên \(\angle EDH = \angle EAH = {50^0}\) (hai góc nội tiếp cùng chắn cung EH)
\( \Rightarrow \angle EDB = \angle BDH + \angle EDH = 90^\circ + 50^\circ = 140^\circ \)
c) Đường thẳng qua E và vuông góc với AB cắt tia AO tại M. Chứng minh \(DM \bot AE.{\mkern 1mu} \)
Kẻ tiếp tuyến Ax của đường tròn \(\left( O \right) \Rightarrow Ax \bot AO\) (tính chất)
Do ADHE nội tiếp nên \(\angle ADE = \angle AHE\) (hai góc nội tiếp cùng chắn cung AE)
Mà \(\angle AHE = \angle ACH\) (cùng phụ với \(\angle EHC\))
\( \Rightarrow \angle ADE = \angle ACH = \angle ACB{\mkern 1mu} {\mkern 1mu} \left( { = \angle AHE} \right)\)
Mà \(\angle ACB = \angle BAx\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB)
\( \Rightarrow \angle BAx = \angle ADE{\mkern 1mu} {\mkern 1mu} \left( { = \angle ACB} \right)\), mà hai góc này ở vị trí hai góc so le trong bằng nhau.
\( \Rightarrow Ax\parallel DE\) (dhnb)
Mà \(Ax \bot AO\) (theo cách vẽ) nên \(DE \bot AO\) (từ vuông góc đến song song).
Xét \(\Delta ADE\) có \(DE \bot AO\), \(EM \bot AB\left( {gt} \right)\), DE cắt AO tại M nên M là trực tâm của \(\Delta ADE\).
\( \Rightarrow DM \bot AE\) (đpcm).













Danh sách bình luận