Đề thi vào 10 môn Toán Bình Thuận năm 2018
Tải vềCâu 1 (1,0 điểm). Rút gọn biểu thức:
Đề bài
Câu 1 (1,0 điểm). Rút gọn biểu thức: \(A = \left( {\sqrt 6 + \sqrt 2 } \right).\sqrt 2 + \sqrt {16} - \sqrt {12} .\)
Câu 2 (2,0 điểm). Giải phương trình và hệ phương trình sau:
a) \({x^2} - 3x - 10 = 0\) b) \(\left\{ \begin{array}{l}2x + y = 4\\3x - y = 1\end{array} \right..\)
Câu 3 (2,0 điểm). Cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right).\)
a) Vẽ đồ thị hàm số \(\left( P \right)\) trên mặt phẳng tọa độ \(\left( {Oxy} \right).\)
b) Tìm tham số \(m\) để phương trình đường thẳng \(\left( d \right):\;\;y = \left( {{m^2} - 4} \right)x + {m^2} - 3\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.
Bài 4 (1,0 điểm). Quãng đường AB dài 120 km. Hai ô tô khởi hành cùng một lúc từ A đến B. Mỗi giờ ô tô thứ nhất chạy được nhanh hơn ô tô thứ hai 12km nên đến B trước ô tô thứ hai 30 phút. Tính vận tốc của ô tô thứ nhất.
Bài 5 (4,0 điểm) Cho đường tròn \(\left( {O;R} \right)\) và điểm M ở ngoài đường tròn \(\left( O \right)\) sao cho \(OM = 2R\). Từ điểm M vẽ hai tiếp tuyến MA, MB với đường tròn \(\left( O \right)\) (A, B là các tiếp điểm).
a) Chứng minh tứ giác AOBM nội tiếp
b) Tính độ dài đoạn thẳng MA theo R và tính số đo \(\angle AOM\).
c) Từ M vẽ cát tuyến MCD đến đường tròn \(\left( O \right)\) (cát tuyến MCD không đi qua tâm và \(MC < MD\)). Chứng minh \(M{A^2} = MC.MD\).
d) AB cắt MO tại H. Chứng minh \(\angle HDC = \angle HOC\)
Lời giải
Câu 1:
Phương pháp:
+) Sử dụng công thức: \(\sqrt A .\sqrt B = \sqrt {AB} ,\;\;\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\;\;khi\;\;A \ge 0\\ - A\;\;khi\;\;A < 0\end{array} \right..\)
Cách giải:
Rút gọn biểu thức: \(A = \left( {\sqrt 6 + \sqrt 2 } \right).\sqrt 2 + \sqrt {16} - \sqrt {12} .\)
\(\begin{array}{l}A = \left( {\sqrt 6 + \sqrt 2 } \right).\sqrt 2 + \sqrt {16} - \sqrt {12} \\\;\;\; = \sqrt {6.2} + \sqrt {2.2} + \sqrt {{4^2}} - \sqrt {12} \\\;\;\; = \sqrt {12} + 2 + 4 - \sqrt {12} \\\;\;\; = 6.\end{array}\)
Câu 2:
Phương pháp:
a) Giải phương trình bằng công thức nghiệm của phương trình bậc hai.
b) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
Cách giải:
Giải phương trình và hệ phương trình sau:
a) \({x^2} - 3x - 10 = 0\)
Ta có: \(\Delta = {3^2} + 4.10 = 49 > 0 \Rightarrow \) phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{3 - \sqrt {49} }}{2} = - 2\\{x_2} = \dfrac{{3 + \sqrt {49} }}{2} = 5\end{array} \right..\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 2;\;5} \right\}.\)
b) \(\left\{ \begin{array}{l}2x + y = 4\\3x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4 - 2x\\5x = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 4 - 2.1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..\)
Vậy hệ phương trình có nghiệm \(\left( {x;\;y} \right) = \left( {1;\;2} \right).\)
Câu 3:
Phương pháp:
+) Lập bảng giá trị các điểm mà đồ thị hàm số đi qua sau đó vẽ đồ thị hàm số.
+) Lập phương trình hoành độ giao điểm \(\left( * \right)\) của đường thẳng \(\left( d \right)\) và đồ thị hàm số \(\left( P \right).\)
Đường thẳng \(\left( d \right)\) cắt đồ thị hàm số \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
Cách giải:
Cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right).\)
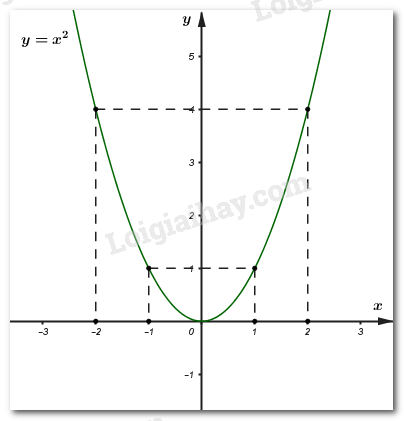
a) Vẽ đồ thị hàm số \(\left( P \right)\) trên mặt phẳng tọa độ \(\left( {Oxy} \right).\)
Ta có bảng giá trị:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
\(y = {x^2}\) |
4 |
1 |
0 |
1 |
4 |
Vậy đồ thị hàm số \(\left( P \right):\;\;y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\;4} \right),\;\;\left( { - 1;\;1} \right),\;\left( {0;\;0} \right),\;\;\left( {1;\;1} \right),\;\left( {2;\;4} \right).\)
b) Tìm tham số \(m\) để phương trình đường thẳng \(\left( d \right):\;\;y = \left( {{m^2} - 4} \right)x + {m^2} - 3\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.
Phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và đồ thị hàm số \(\left( P \right)\) là:
\({x^2} = \left( {{m^2} - 4} \right)x + {m^2} - 3 \Leftrightarrow {x^2} - \left( {{m^2} - 4} \right)x - {m^2} + 3 = 0.\;\;\;\;\left( * \right)\)
Đường thẳng \(\left( d \right)\) cắt đồ thị hàm số \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta > 0\\ \Leftrightarrow {\left( {{m^2} - 4} \right)^2} + 4\left( {{m^2} - 3} \right) > 0\\ \Leftrightarrow {m^4} - 8{m^2} + 16 + 4{m^2} - 12 > 0\\ \Leftrightarrow {m^4} - 4{m^2} + 4 > 0\\ \Leftrightarrow {\left( {{m^2} - 2} \right)^2} > 0\\ \Leftrightarrow {m^2} - 2 \ne 0\\ \Leftrightarrow m \ne \pm \sqrt 2 .\end{array}\)
Vậy \(m \ne \pm \sqrt 2 \) thỏa mãn điều kiện bài toán.
Câu 4.
Phương pháp:
Gọi vận tốc của ô tô thứ nhất là x \(\left( {x > 12} \right)\,\,\left( {km/h} \right)\)
Tính vận tốc của ô tô thứ hai.
Tính thời gian đi từ A đến B của 2 xe.
Dựa vào giả thiết ô tô thứ nhất đến B trước ô tô thứ hai 30 phút = \(\dfrac{1}{2}\,\,\left( h \right)\) lập và giải phương trình.
Cách giải:
Quãng đường AB dài 120 km. Hai ô tô khởi hành cùng một lúc từ A đến B. Mỗi giờ ô tô thứ nhất chạy được nhanh hơn ô tô thứ hai 12km nên đến B trước ô tô thứ hai 30 phút. Tính vận tốc của ô tô thứ nhất.
Gọi vận tốc của ô tô thứ nhất là \(x\;\;\left( {x > 12} \right)\,\,\left( {km/h} \right)\)
Khi đó vận tốc của ô tô thứ hai là \(x - 12\,\,\left( {km/h} \right)\)
Thời gian ô tô thứ nhất đi từ A đến B là \(\dfrac{{120}}{x}\,\,\left( h \right)\)
Thời gian ô tô thứ hai đi từ A đến B là \(\dfrac{{120}}{{x - 12}}\,\,\left( h \right)\)
Vì ô tô thứ nhất đến B trước ô tô thứ hai 30 phút = \(\dfrac{1}{2}\,\,\left( h \right)\) nên ta có phương trình:
\(\begin{array}{l}\;\;\;\;\;\dfrac{{120}}{{x - 12}} - \dfrac{{120}}{x} = \dfrac{1}{2}\\ \Leftrightarrow 240x - 240\left( {x - 12} \right) = x\left( {x - 12} \right)\\ \Leftrightarrow 240x - 240x + 2880 = {x^2} - 12x\\ \Leftrightarrow {x^2} - 12x - 2880 = 0\\ \Leftrightarrow \left( {x - 60} \right)\left( {x + 48} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 60 = 0\\x + 48 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 60\,\,\left( {tm} \right)\\x = - 48\,\,\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy vận tốc của ô tô thứ nhất là 60 km/h.
Bài 5.
Phương pháp:
a) Chứng minh tứ giác AOBM có tổng hai góc đối bằng 1800.
b) Sử dụng định lí Pytago tính MA, tính cos góc AOM.
c) Chứng minh tam giác MAC và tam giác MDA đồng dạng.
d) Chứng minh tứ giác ODCH nội tiếp.
Cách giải:
Cho đường tròn \(\left( {O;R} \right)\) và điểm M ở ngoài đường tròn \(\left( O \right)\) sao cho \(OM = 2R\). Từ điểm M vẽ hai tiếp tuyến MA, MB với đường tròn \(\left( O \right)\) (A, B là các tiếp điểm).
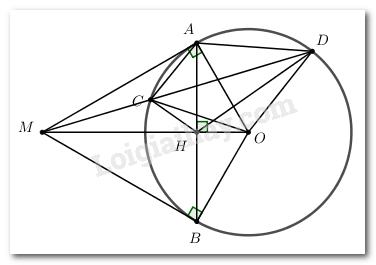
a) Chứng minh tứ giác AOBM nội tiếp
Ta có \(\angle OAM = \angle OBM = {90^0} \Rightarrow \angle OAM + \angle OBM = {180^0} \Rightarrow \) Tứ giác OAMB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Tính độ dài đoạn thẳng MA theo R và tính số đo \(\angle AOM\).
Áp dụng định lí Pytago trong tam giác vuông OAM có: \(AM = \sqrt {O{M^2} - O{A^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 \)
Ta có: \(\cos \angle AOM = \dfrac{{OA}}{{OM}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \Rightarrow \angle AOM = {60^0}\)
c) Từ M vẽ cát tuyến MCD đến đường tròn \(\left( O \right)\) (cát tuyến MCD không đi qua tâm và \(MC < MD\)). Chứng minh \(M{A^2} = MC.MD\).
Xét tam giác MAC và MDA có:
\(\angle MAC = \angle MDA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AC);
\(\angle AMD\) chung
\( \Rightarrow \Delta MAC \sim \Delta MDA\,\,\left( {g.g} \right) \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MC}}{{MA}} \Leftrightarrow M{A^2} = MC.MD\;\;\;\left( {dpcm} \right).\)
d) AB cắt MO tại H. Chứng minh \(\angle HDC = \angle HOC\)
Áp dụng hệ thức lượng trong tam giác vuông OAM có \(M{A^2} = MH.MO\)
\( \Rightarrow MC.MD = MH.MO \Rightarrow \dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MD}}\)
Xét tam giác MCH và tam giác MOD có:
\(\angle OMD\) chung;
\(\dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MD}}\,\,\left( {cmt} \right)\)
\( \Rightarrow \Delta MCH \sim \Delta MOD\,\,\left( {c.g.c} \right) \Rightarrow \angle MHC = \angle ODM = \angle ODC\) (hai góc tương ứng)
Mà \(\angle MHC + \angle OHC = {180^0}\) (kề bù) \( \Rightarrow \angle OHC + \angle ODC = {180^0} \Rightarrow \) Tứ giác ODCH là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
\( \Rightarrow \angle HDC = \angle HOC\) (Hai góc nội tiếp cùng chắn cung HC).













Danh sách bình luận