Đề thi vào 10 môn Toán An Giang năm 2021
Tải vềCâu 1 (3 điểm): Giải các phương trình và hệ phương trình sau đây:
Đề bài
Câu 1 (3 điểm): Giải các phương trình và hệ phương trình sau đây:
a) \(\left( {\sqrt 2 + 1} \right)x - \sqrt 2 = 2\)
b) \({x^4} + {x^2} - 6 = 0\)
c) \(\left\{ \begin{array}{l}2x + y = 11\\x - y = 4\end{array} \right.\)
Câu 2 (2 điểm): Cho hai hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right)\) và \(y = x + 2\) có đồ thị là đường thẳng \(\left( d \right).\)
a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng một hệ trục tọa độ.
b) Bằng phép tính, tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right).\)
Câu 3 (2 điểm): Cho phương trình bậc hai \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 3m - 4 = 0\) (\(m\) là tham số, \(x\) là ẩn số).
a) Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1};\,{x_2}.\)
b) Đặt \(A = x_1^2 + x_2^2 - {x_1}{x_2}.\) Tính \(A\) theo \(m\) và tìm \(m\) để \(A = 18.\)
Câu 4 (2 điểm): Cho bốn điểm \(A,\,\,B,\,\,C,\,\,D\) theo thứ tự lần lượt nằm trên nửa đường tròn đường kính \(AD.\) Gọi \(E\) là giao điểm của \(AC\) và \(BD.\) Kẻ \(EF \bot AD\,\,\,\left( {F \in AD} \right).\)
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
b) Chứng minh \(BD\) là tia phân giác của \(\angle CBF.\)
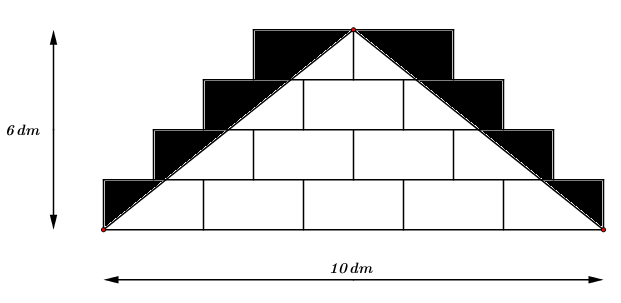
Câu 5 (1 điểm): Một bức tường được xây bằng các viên gạch hình chữ nhật bằng nhau và được bố trí như hình vẽ bên dưới. Phần sơn màu (tô đậm) là phần ngoài của một tam giác có cạnh đáy \(10\,dm\) và chiếu cao \(6\,dm.\) Tính diện tích phần tô đậm.
Lời giải chi tiết
Câu 1
Phương pháp:
a) Đưa phương trình về dạng \(ax + b = 0\) sau đó giải
b) Đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\), đưa phương trình ban đầu về dạng phương trình bậc hai ẩn \(t\), sau đó giải phương trình
c) Giải hệ phương trình bằng phương pháp cộng đại số
Cách giải:
a)
\(\begin{array}{l}\,\,\,\,\,\left( {\sqrt 2 + 1} \right)x - \sqrt 2 = 2\\ \Leftrightarrow \left( {\sqrt 2 + 1} \right)x = 2 + \sqrt 2 \\ \Leftrightarrow \left( {\sqrt 2 + 1} \right)x = \sqrt 2 \left( {1 + \sqrt 2 } \right)\\ \Leftrightarrow x = \sqrt 2 .\end{array}\)
Vậy phương trình có nghiệm:\(x = \sqrt 2 .\)
b) \({x^4} + {x^2} - 6 = 0\)
Đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\)
\( \Rightarrow \) Phương trình \( \Leftrightarrow {t^2} + t - 6 = 0\)
\(\begin{array}{l} \Leftrightarrow {t^2} - 2t + 3t - 6 = 0\\ \Leftrightarrow t\left( {t - 2} \right) + 3\left( {t - 2} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {t + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t - 2 = 0\\t + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\left( {tm} \right)\\t = - 3\,\,\,\left( {ktm} \right)\end{array} \right.\\ \Leftrightarrow {x^2} = 2\\ \Leftrightarrow x = \pm \sqrt 2 .\end{array}\)
Vậy phương trình có tập nghiệm: \(S = \left\{ { - \sqrt 2 ;\,\,\sqrt 2 } \right\}.\)
c) \(\left\{ \begin{array}{l}2x + y = 11\\x - y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 4\\3x = 15\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = x - 4\\x = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(S = \left( {5;\,\,1} \right).\)
Câu 2
Phương pháp:
a) Lập bảng giá trị để vẽ đồ thị
b) Tính biệt thức đen – ta, sau đó vận dụng điều kiện có 2 nghiệm phân biệt của phương trình bậc hai một ẩn
Cách giải:
a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng một hệ trục tọa độ.
+) Vẽ đồ thị hàm số: \(\left( P \right):\,\,\,y = {x^2}\)
Ta có bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = {x^2}\) |
\(4\) |
\(1\) |
\(0\) |
\(1\) |
\(4\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,\,y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\,\,4} \right),\,\,\left( { - 1;\,\,1} \right)\,,\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,1} \right)\) và \(\left( {2;\,\,4} \right).\)
+) Vẽ đồ thị hàm số: \(\left( d \right):\,\,y = x + 2\)
Ta có bảng giá trị:
|
\(x\) |
\(0\) |
\( - 2\) |
|
\(y = x + 2\) |
\(2\) |
\(0\) |
Vậy đồ thị hàm số \(\left( d \right):\,\,y = x + 2\) là đường thẳng đi qua các điểm \(\left( {0;\,\,2} \right)\) và \(\left( { - 2;\,\,0} \right).\)
Đồ thị hàm số:
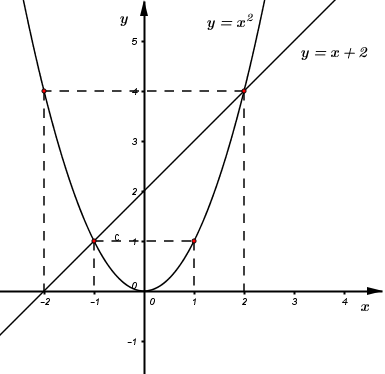
b) Bằng phép tính, tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right).\)
Phương trình hoành độ giao điểm của hai đồ thị hàm số \(\left( P \right)\) và \(\left( d \right)\) là:
\(\begin{array}{l}\,\,\,\,\,\,{x^2} = x + 2\\ \Leftrightarrow {x^2} - x - 2 = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\end{array}\)
Với \(x = - 1\)\( \Rightarrow y = {\left( { - 1} \right)^2} = 1.\)
Với \(x = 2\) \( \Rightarrow y = {2^2} = 4.\)
Vậy đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(\left( { - 1;\,\,1} \right)\) và \(\left( {2;\,\,4} \right).\)
Câu 3
Phương pháp:
a) Tính biệt thức đen – ta, sau đó vận dụng điều kiện có 2 nghiệm phân biệt của phương trình bậc hai một ẩn
b) Áp dụng ứng dụng của hệ thức Vi – ét và giả thiết của đề bài để tìm \(m\)
Cách giải:
a) Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1};\,{x_2}.\)
\({x^2} - 2\left( {m - 1} \right)x + {m^2} - 3m - 4 = 0\,\,\,\,\,\left( * \right)\)
Phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {m - 1} \right)^2} - \left( {{m^2} - 3m - 4} \right) > 0\\ \Leftrightarrow {m^2} - 2m + 1 - {m^2} + 3m + 4 > 0\\ \Leftrightarrow m + 5 > 0\\ \Leftrightarrow m > - 5.\end{array}\)
Vậy với \(m > - 5\) thì phương trình đã cho có hai nghiệm phân biệt \({x_1};\,\,{x_2}.\)
b) Đặt \(A = x_1^2 + x_2^2 - {x_1}{x_2}.\) Tính \(A\) theo \(m\) và tìm \(m\) để \(A = 18.\)
Với \(m > - 5\) thì phương trình đã cho có hai nghiệm phân biệt \({x_1};\,\,{x_2}.\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right) = 2m - 2\\{x_1}{x_2} = {m^2} - 3m - 4\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}A = x_1^2 + x_2^2 - {x_1}{x_2}\\\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - {x_1}{x_2}\\\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\\\,\,\,\,\, = 4{\left( {m - 1} \right)^2} - 3\left( {{m^2} - 3m - 4} \right)\\\,\,\,\,\, = 4\left( {{m^2} - 2m + 1} \right) - 3{m^2} + 9m + 12\\\,\,\,\,\,\, = 4{m^2} - 8m + 4 - 3{m^2} + 9m + 12\\\,\,\,\,\,\, = {m^2} + m + 16.\end{array}\)
\(\begin{array}{l} \Rightarrow A = 18\\ \Leftrightarrow {m^2} + m + 16 = 18\\ \Leftrightarrow {m^2} + m - 2 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\,\,\,\left( {tm} \right)\\m = - 2\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m \in \left\{ { - 2;\,\,1} \right\}\) thỏa mãn bài toán.
Câu 4
Phương pháp:
a) Áp dụng dấu hiệu nhận biết của tứ giác nội tiếp có tổng hai góc đối bằng \({180^0}\)
b) Sử dụng tính chất bắc cầu để chứng minh \( \Rightarrow BD\) là phân giác của \(\angle FBC.\,\,\)
Cách giải:
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
Ta có: \(\angle ABD\) là góc nội tiếp chắn nửa đường tròn đường kính \(AD\)
\( \Rightarrow \angle ABD = {90^0}\) hay \(\angle ABE = {90^0}\)
Xét tứ giác \(ABEF\) ta có: \(\angle ABE + \angle AFE = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow ABEF\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
b) Chứng minh \(BD\) là tia phân giác của \(\angle CBF.\)
Vì \(ABEF\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle FBE = \angle FAE\) (hai góc nội tiếp cùng chắn cung \(EF\))
Hay \(\angle CAD = \angle FBD.\)
Lại có: \(\angle CBD = \angle CAD\) (hai góc nội tiếp cùng chắn cung \(CD\))
\( \Rightarrow \angle CBD = \angle FBD\,\,\,\left( { = \angle CAD} \right)\)
\( \Rightarrow BD\) là phân giác của \(\angle FBC.\,\,\,\left( {dpcm} \right).\)
Câu 5
Phương pháp:
Tính diện tích của 1 viên gạch từ đó tính diện tích của bức tường, tính diện tich của hình tam giác và từ đó suy ra phần diện tích cần tính.
Cách giải:
Chiều rộng của một viên gạch là: \(6:4 = 1,5\,\,\left( {dm} \right).\)
Chiều dài của một viên gạch là: \(10:5 = 2\,\,\left( {dm} \right).\)
Diện tích của một viên gạch là: \(1,5.2 = 3\,\,\,\left( {d{m^2}} \right).\)
Tổng số viên gạch để xây bức tường là: \(2 + 3 + 4 + 5 = 14\) (viên).
Diện tích của bức tường đã xây là: \(3.14 = 42\,\,\left( {d{m^2}} \right).\)
Diện tích tam giác trong hình là: \(\dfrac{1}{2}.6.10 = 30\,\,\left( {d{m^2}} \right).\)
Diện tích phần sơn màu là: \(42 - 30 = 12\,\,\,\left( {d{m^2}} \right).\)













Danh sách bình luận