Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3
Đề bài
Cho khối nón có độ dài đường cao bằng \(2a\) và bán kính đáy bằng \(a.\) Thể tích của khối nón đã cho bằng:
-
A.
\(\dfrac{{2\pi {a^3}}}{3}\)
-
B.
\(\dfrac{{4\pi {a^3}}}{3}\)
-
C.
\(\dfrac{{\pi {a^3}}}{3}\)
-
D.
\(2\pi {a^3}\)
Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\,\,SA = a\) và \(SA \bot \left( {ABCD} \right).\) Thể tích khối chóp \(SABCD\) bằng
-
A.
\(\dfrac{{{a^3}}}{6}\)
-
B.
\(\dfrac{{2{a^3}}}{6}\)
-
C.
\({a^3}\)
-
D.
\(\dfrac{{{a^3}}}{3}\)
Trong không gian \(Oxyz,\) một vecto chỉ phương của đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{{z - 3}}{{ - 5}}\) có tọa độ là:
-
A.
\(\left( {1;\,\,2; - 5} \right)\)
-
B.
\(\left( {1;\,\,3;\,3} \right)\)
-
C.
\(\left( { - 1;\,\,3; - 3} \right)\)
-
D.
\(\left( { - 1; - 2; - 5} \right)\)
Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:
-
A.
\(2{\log _2}\dfrac{a}{b}\)
-
B.
\(\dfrac{1}{2}{\log _2}\dfrac{a}{b}\)
-
C.
\({\log _2}a - 2{\log _2}b\)
-
D.
\({\log _2}a - {\log _2}\left( {2b} \right)\)
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( { - 2; - 1;\,\,3} \right)\) và \(B\left( {0;\,\,3;\,\,1} \right).\) Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của \(AB.\) Một vecto pháp tuyến của \(\left( \alpha \right)\) có tọa độ là:
-
A.
\(\left( {2;\,\,4; - 1} \right)\)
-
B.
\(\left( {1;\,\,2; - 1} \right)\)
-
C.
\(\left( { - 1;\,\,1;\,\,2} \right)\)
-
D.
\(\left( {1;\,\,0;\,\,1} \right)\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 1,\,\,{u_2} = - 2.\) Mệnh đề nào sau đây đúng?
-
A.
\({u_{2019}} = - {2^{2018}}\)
-
B.
\({u_{2019}} = {2^{2019}}\)
-
C.
\({u_{2019}} = - {2^{2019}}\)
-
D.
\({u_{2019}} = {2^{2018}}\)
Hình dưới đây là đồ thị của hàm số nào?

-
A.
\(y = {x^2} - 2\)
-
B.
\(y = {x^4} + {x^2} - 2\)
-
C.
\(y = {x^4} - {x^2} - 2\)
-
D.
\(y = {x^2} + x - 2\)
Trong không gian \(Oxyz,\) cho điểm \(I\left( {1;\,\,2;\,\,5} \right)\) và mặt phẳng \(\left( \alpha \right):\,\,\,x - 2y + 2z + 2 = 0.\) Phương trình mặt cầu tâm \(I\) và tiếp xúc với \(\left( \alpha \right)\) là:
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 3\)
-
B.
\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 5} \right)^2} = 3\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 9\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 5} \right)^2} = 9\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Trên đoạn \(\left[ { - 3;\,3} \right],\) hàm số đã cho có mấy điểm cực trị?
-
A.
$4$
-
B.
$5$
-
C.
$2$
-
D.
$3$
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục bất kì trên đoạn \(\left[ {a;\,\,b} \right].\) Mênh đề nào sau đây đúng?
-
A.
\(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
-
B.
\(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
-
C.
\(\left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} } \right|dx = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
-
D.
\(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \left| {\int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} } \right|\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng:
-
A.
\(\left( {0;\,\,2} \right)\)
-
B.
\(\left( { - 2;\,0} \right)\)
-
C.
\(\left( { - 3; - 1} \right)\)
-
D.
\(\left( {2;\,3} \right)\)
Tất cả các nguyên hàm của hàm \(f\left( x \right) = \dfrac{1}{{\sqrt {3x - 2} }}\) là:
-
A.
\(2\sqrt {3x - 2} + C\)
-
B.
\(\dfrac{2}{3}\sqrt {3x - 2} + C\)
-
C.
\( - \dfrac{2}{3}\sqrt {3x - 2} + C\)
-
D.
\( - 2\sqrt {3x - 2} + C\)
Khi đặt \({3^x} = t\) thì phương trình \({9^{x + 1}} - {3^{x + 1}} - 30 = 0\) trở thành:
-
A.
\(3{t^2} - t - 10 = 0\)
-
B.
\(9{t^2} - 3t - 10 = 0\)
-
C.
\({t^2} - t - 10 = 0\)
-
D.
\(2{t^2} - t - 1 = 0\)
Từ các chữ số \(1;\,\,2;\,\,3;\,\,......;\,\,9\) lập được bao nhiêu số có 3 chữ số đôi một khác nhau.
-
A.
\({3^9}\)
-
B.
\(A_9^3\)
-
C.
\({9^3}\)
-
D.
\(C_9^3\)
Cho số phức \(z = - 2 + i.\) Trong hình bên điểm biểu diễn số phức \(\overline z \) là:
-
A.
M
-
B.
Q
-
C.
P
-
D.
N
Trong không gian \(Oxyz,\) cho hai đường thẳng \({\Delta _1}:\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{{y + 2}}{1} = \dfrac{{z - 3}}{2}\) và \({\Delta _2}:\,\,\dfrac{{x + 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{{ - 4}}.\) Góc giữa hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) bằng:
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({135^0}\)
Cho số phức \(z\) thỏa mãn \(z + 2\overline z = 6 + 2i.\) Điểm biểu diễn số phức \(z\) có tọa độ là:
-
A.
\(\left( {2; - 2} \right)\)
-
B.
\(\left( { - 2; - 2} \right)\)
-
C.
\(\left( {2;\,\,2} \right)\)
-
D.
\(\left( { - 2;\,\,2} \right)\)
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\,\,\dfrac{{x - 2}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{z}{2}\) và mặt phẳng \(\left( P \right):\,\,x + 2y - z - 5 = 0.\) Tọa độ giao điểm của \(d\) và \(\left( P \right)\) là:
-
A.
\(\left( {2;\,\,1; - 1} \right)\)
-
B.
\(\left( {3; - 1; - 2} \right)\)
-
C.
\(\left( {1;\,\,3; - 2} \right)\)
-
D.
\(\left( {1;\,\,3;\,\,2} \right)\)
Bất phương trình \({\log _4}\left( {{x^2} - 3x} \right) > {\log _2}\left( {9 - x} \right)\) có bao nhiêu nghiệm nguyên?
-
A.
vô số
-
B.
$1$
-
C.
$4$
-
D.
$3$
Hàm số \(y = {\left( {{x^3} - 3x} \right)^e}\) có bao nhiêu điểm cực trị?
-
A.
$2$
-
B.
$0$
-
C.
$3$
-
D.
$1$
Gọi \(\left( D \right)\) là hình phẳng giới hạn bởi các đường \(y = {2^x},\,\,y = 0,\,\,x = 0\) và \(x = 2.\) Thể tích \(V\) của khối tròn xoay tạo thành khi quay \(\left( D \right)\) quanh trục \(Ox\) được xác định bởi công thức:
-
A.
\(V = \pi \int\limits_0^2 {{2^{x + 1}}dx} \)
-
B.
\(V = \int\limits_0^2 {{2^{x + 1}}dx} \)
-
C.
\(V = \int\limits_0^2 {{4^x}dx} \)
-
D.
\(V = \pi \int\limits_0^2 {{4^x}dx} \)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:
Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Đồ thị hàm số \(y = \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}}\) có bao nhiêu đường tiệm cận?
-
A.
$4$
-
B.
$3$
-
C.
$1$
-
D.
$2$
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
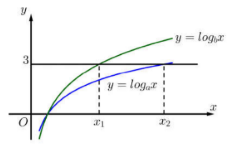
-
A.
\(\dfrac{1}{2}\)
-
B.
\(\sqrt 3 \)
-
C.
\(2\)
-
D.
\(\sqrt[3]{2}\)
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,\,\,AD = 2a,\,AC' = \sqrt 6 a.\) Thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) bằng:
-
A.
\(\dfrac{{\sqrt 3 {a^3}}}{3}\)
-
B.
\(\dfrac{{2{a^3}}}{3}\)
-
C.
\(2{a^3}\)
-
D.
\(2\sqrt 3 {a^3}\)
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} + x} \right){\left( {x - 2} \right)^2}\left( {{2^x} - 4} \right),\,\,\,\forall x \in \mathbb{R}.\) Số điểm cực trị của \(f\left( x \right)\) là:
-
A.
$2$
-
B.
$4$
-
C.
$3$
-
D.
$1$
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Diện tích xung quanh của hình trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông \(ABCD\) và \(A'B'C'D'\) là:
-
A.
\(\sqrt 2 \pi {a^2}\)
-
B.
\(2\pi {a^2}\)
-
C.
\(\pi {a^2}\)
-
D.
\(2\sqrt 2 \pi {a^2}\)
Gọi \({z_1},\,\,{z_2}\) là các nghiệm phức của phương trình \({z^2} - 2z + 3 = 0.\) Modul của \(z_1^3.z_2^4\) bằng:
-
A.
\(81\)
-
B.
\(16\)
-
C.
\(27\sqrt 3 \)
-
D.
\(8\sqrt 2 \)
Gọi \(m,\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2}\) trên đoạn \(\left[ { - 2;\,\,2} \right].\) Giá trị của \(m + M\) bằng:
-
A.
\(2\)
-
B.
\( - 2\)
-
C.
\(0\)
-
D.
\( - 4\)
Cho hình chóp đều \(SABCD\) có \(AB = 2a,\,\,SA = a\sqrt 5 .\) Góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng:
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({75^0}\)
Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng:
-
A.
\(\dfrac{{145}}{{729}}\)
-
B.
\(\dfrac{{448}}{{729}}\)
-
C.
\(\dfrac{{281}}{{729}}\)
-
D.
\(\dfrac{{154}}{{729}}\)
Biết rằng \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) trên khoảng \(\left( { - \infty ; + \infty } \right)\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f'\left( x \right){e^x}\) thỏa mãn \(F\left( 0 \right) = 1\), giá trị của \(F\left( { - 1} \right)\) bằng:
-
A.
\(\dfrac{7}{2}\)
-
B.
\(\dfrac{{5 - e}}{2}\)
-
C.
\(\dfrac{{7 - e}}{2}\)
-
D.
\(\dfrac{5}{2}\)
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(AB = 2a,\,\,AD = a,\,\,SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\). Khoảng cách giữa hai đường thẳng \(SC\) và \(BM\) bằng:
-
A.
\(\dfrac{{3\sqrt 3 a}}{4}\)
-
B.
\(\dfrac{{2\sqrt 3 a}}{3}\)
-
C.
\(\dfrac{{\sqrt 3 a}}{3}\)
-
D.
\(\dfrac{{\sqrt 3 a}}{2}\)
Cho hàm số \(f\left( x \right)\) có bảng xét dấu có đạo hàm như hình bên dưới
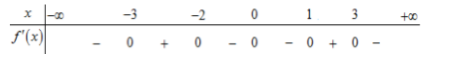
Hàm số \(y = f\left( {1 - 2x} \right)\) đồng biến trên khoảng
-
A.
\(\left( {0;\dfrac{3}{2}} \right)\)
-
B.
\(\left( { - \dfrac{1}{2};1} \right)\)
-
C.
\(\left( { - 2; - \dfrac{1}{2}} \right)\)
-
D.
\(\left( {\dfrac{3}{2};3} \right)\)
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| {w - i} \right| = 2,\,\,z + 2 = iw\). Gọi \({z_1},\,\,{z_2}\) lần lượt là các số phức mà tại đó \(\left| z \right|\) đạt giá trị nhỏ nhất và giá trị lớn nhất. Môđun \(\left| {{z_1} + {z_2}} \right|\) bằng:
-
A.
\(3\sqrt 2 \)
-
B.
\(3\)
-
C.
\(6\)
-
D.
\(6\sqrt 2 \)
Cho \(f\left( x \right) = {\left( {x - 1} \right)^3} - 3x + 3\). Đồ thị hình bên là của hàm số có công thức:
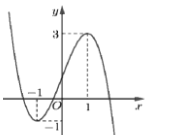
-
A.
\(y = - f\left( {x + 1} \right) - 1\)
-
B.
\(y = - f\left( {x + 1} \right) + 1\)
-
C.
\(y = - f\left( {x - 1} \right) - 1\)
-
D.
\(y = - f\left( {x - 1} \right) + 1\)
Người ta xếp hai quả cầu có cùng bán kính \(r\) vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là \(120\,\,c{m^3}\), thể tích của mỗi khối cầu bằng
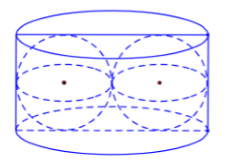
-
A.
\(10\,\,c{m^3}\)
-
B.
\(20\,\,c{m^3}\)
-
C.
\(30\,\,c{m^3}\)
-
D.
\(40\,\,c{m^3}\)
Biết \(\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{{{\cos }^2}x + \sin x\cos x + 1}}{{{{\cos }^4}x + \sin x{{\cos }^3}x}}dx} = a + b\ln 2 + c\ln \left( {1 + \sqrt 3 } \right)\), với \(a,\,\,b,\,\,c\) là các số hữu tỉ. Giá trị của \(abc\) bằng:
-
A.
\(0\)
-
B.
\( - 2\)
-
C.
\( - 4\)
-
D.
\( - 6\)
Trong không gian \(Oxyz\), cho hai đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = - 1 - 2t\\y = t\\z = - 1 + 3t\end{array} \right.,\,\,d':\,\,\left\{ \begin{array}{l}x = 2 + t'\\y = - 1 + 2t'\\z = - 2t'\end{array} \right.\) và mặt phẳng \(\left( P \right):\,\,x + y + z + 2 = 0\). Đường thẳng vuông góc với mặt phẳng \(\left( P \right)\) và cắt hai đường thẳng \(d,\,\,d'\) có phương trình là:
-
A.
\(\dfrac{{x - 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{1}\)
-
B.
\(\dfrac{{x - 1}}{1} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{{z - 1}}{{ - 4}}\)
-
C.
\(\dfrac{{x + 2}}{1} = \dfrac{{y + 1}}{1} = \dfrac{{z - 1}}{1}\)
-
D.
\(\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{2} = \dfrac{{z - 4}}{2}\)
Có bao nhiêu số nguyên \(m\) để phương trình \(x + 3 = m{e^x}\) có 2 nghiệm phân biệt?
-
A.
$7$
-
B.
$6$
-
C.
$5$
-
D.
Vô số
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {x - 1} \right) + {x^2} - 2x\) đồng biến trên khoảng?
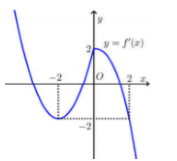
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( { - 1;0} \right)\)
-
C.
\(\left( {0;1} \right)\)
-
D.
\(\left( { - 2; - 1} \right)\)
Có bao nhiêu số nguyên \(a \in \left( { - 2019;2019} \right)\) để phương trình \(\dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} = x + a\) có hai nghiệm phân biệt?
-
A.
$0$
-
B.
$2022$
-
C.
$2014$
-
D.
$2015$
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( 0 \right) = 3\) và \(f\left( x \right) + f\left( {2 - x} \right) = {x^2} - 2x + 2\,\,\forall x \in \mathbb{R}\). Tích phân \(\int\limits_0^2 {xf'\left( x \right)dx} \) bằng:
-
A.
\( - \dfrac{4}{3}\)
-
B.
\(\dfrac{2}{3}\)
-
C.
\(\dfrac{5}{3}\)
-
D.
\(\dfrac{{ - 10}}{3}\)
Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) (với \(m\) là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?
-
A.
$2$
-
B.
$3$
-
C.
$5$
-
D.
$4$
Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích bằng \(V\). Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,E,\,\,F\) lần lượt là tâm các hình bình hành \(ABCD,\,\,A'B'C'D',\,\,ABB'A',\,\,BCC'B',\,\,CDD'C',\,\,DAA'D'\). Thể tích khối đa diện có các đỉnh \(M,\,\,P,\,\,Q,\,\,E,\,\,F,\,\,N\) bằng:
-
A.
\(\dfrac{V}{4}\)
-
B.
\(\dfrac{V}{2}\)
-
C.
\(\dfrac{V}{6}\)
-
D.
\(\dfrac{V}{3}\)
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh \(40\,\left( {cm} \right)\) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \(4{x^2} = {y^4}\) và \(4{\left( {\left| x \right| - 1} \right)^3} = {y^2}\) để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?
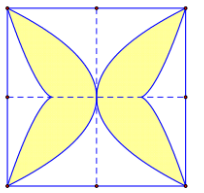
-
A.
\(506\,\,\left( {c{m^2}} \right)\)
-
B.
\(747\,\,\left( {c{m^2}} \right)\)
-
C.
\(507\,\,\left( {c{m^2}} \right)\)
-
D.
\(746\,\,\left( {c{m^2}} \right)\)
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| z \right| = 2,\,\,\left| {iw - 2 + 5i} \right| = 1\). Giá trị nhỏ nhất của \(\left| {{z^2} - wz - 4} \right|\) bằng:
-
A.
\(4\)
-
B.
\(2\left( {\sqrt {29} - 3} \right)\)
-
C.
\(8\)
-
D.
\(2\left( {\sqrt {29} - 5} \right)\)
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
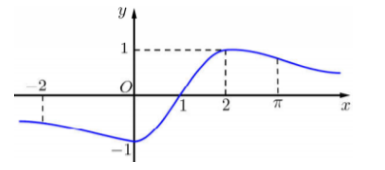
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
-
A.
\(m < f\left( 0 \right)\)
-
B.
\(m < f\left( 1 \right) - 1\)
-
C.
\(m < f\left( { - 1} \right) + 1\)
-
D.
\(m < f\left( 2 \right)\)
Trong không gian Oxyz , cho đường thẳng \(d:\,\,\dfrac{{x - 3}}{2} = \dfrac{{y - 4}}{1} = \dfrac{{z - 2}}{1}\) và 2 điểm \(A\left( {6;3; - 2} \right)\); \(B\left( {1;0; - 1} \right)\). Gọi \(\Delta \) là đường thẳng đi qua \(B\), vuông góc với \(d\) và thỏa mãn khoảng cách từ \(A\) đến \(\Delta \) là nhỏ nhất. Một vectơ chỉ phương của \(\Delta \) có tọa độ :
-
A.
\(\left( {1;1; - 3} \right)\)
-
B.
\(\left( {1; - 1; - 1} \right)\)
-
C.
\(\left( {1;2; - 4} \right)\)
-
D.
\(\left( {2; - 1; - 3} \right)\)
Lời giải và đáp án
Cho khối nón có độ dài đường cao bằng \(2a\) và bán kính đáy bằng \(a.\) Thể tích của khối nón đã cho bằng:
-
A.
\(\dfrac{{2\pi {a^3}}}{3}\)
-
B.
\(\dfrac{{4\pi {a^3}}}{3}\)
-
C.
\(\dfrac{{\pi {a^3}}}{3}\)
-
D.
\(2\pi {a^3}\)
Đáp án : A
Công thức tính thể tích của khối nón có bán kính đáy và chiều cao \(h:\;\;\;V = \dfrac{1}{3}\pi {R^2}h.\)
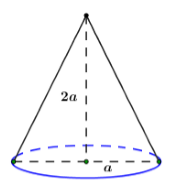
Thể tích khối nón đã cho là: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .2a.{a^2} = \dfrac{{2\pi {a^3}}}{3}.\)
Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\,\,SA = a\) và \(SA \bot \left( {ABCD} \right).\) Thể tích khối chóp \(SABCD\) bằng
-
A.
\(\dfrac{{{a^3}}}{6}\)
-
B.
\(\dfrac{{2{a^3}}}{6}\)
-
C.
\({a^3}\)
-
D.
\(\dfrac{{{a^3}}}{3}\)
Đáp án : D
Công thức tính thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là:\(V = \dfrac{1}{3}Sh.\)
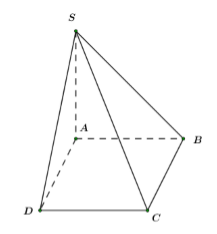
Ta có thể tích của khối chóp đã cho là:
\({V_{SABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a.{a^2} = \dfrac{{{a^3}}}{3}.\)
Trong không gian \(Oxyz,\) một vecto chỉ phương của đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{{z - 3}}{{ - 5}}\) có tọa độ là:
-
A.
\(\left( {1;\,\,2; - 5} \right)\)
-
B.
\(\left( {1;\,\,3;\,3} \right)\)
-
C.
\(\left( { - 1;\,\,3; - 3} \right)\)
-
D.
\(\left( { - 1; - 2; - 5} \right)\)
Đáp án : A
Đường thẳng \(d:\,\,\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\) nhận vecto \(\overrightarrow u = \left( {a;\,b;\,c} \right)\) làm 1 VTCP.
Đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{{z - 3}}{{ - 5}}\) nhận vecto \(\left( {1;\,2; - 5} \right)\) làm 1 VTCP
Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:
-
A.
\(2{\log _2}\dfrac{a}{b}\)
-
B.
\(\dfrac{1}{2}{\log _2}\dfrac{a}{b}\)
-
C.
\({\log _2}a - 2{\log _2}b\)
-
D.
\({\log _2}a - {\log _2}\left( {2b} \right)\)
Đáp án : C
Sử dụng các công thức: \(lo{g_a}\dfrac{b}{c} = lo{g_a}b - lo{g_a}c;\,\,\,{\log _{{a^m}}}b = \dfrac{1}{m}{\log _a}b;\,\,\,{\log _a}{b^n} = n{\log _a}b.\)
Ta có: \({\log _2}\dfrac{a}{{{b^2}}} = {\log _2}a - {\log _2}{b^2} = {\log _2}a - 2{\log _a}b.\)
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( { - 2; - 1;\,\,3} \right)\) và \(B\left( {0;\,\,3;\,\,1} \right).\) Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của \(AB.\) Một vecto pháp tuyến của \(\left( \alpha \right)\) có tọa độ là:
-
A.
\(\left( {2;\,\,4; - 1} \right)\)
-
B.
\(\left( {1;\,\,2; - 1} \right)\)
-
C.
\(\left( { - 1;\,\,1;\,\,2} \right)\)
-
D.
\(\left( {1;\,\,0;\,\,1} \right)\)
Đáp án : B
Mặt phẳng trung trực \(\left( \alpha \right)\) của đoạn thẳng \(AB\) nhận \(\overrightarrow {AB} \) làm một VTPT.
Mặt phẳng trung trực \(\left( \alpha \right)\) của đoạn thẳng \(AB\) nhận \(\overrightarrow {AB} \) làm một VTPT.
Ta có: \(\overrightarrow {AB} = \left( {2;\,\,4;\,\, - 2} \right) = 2\left( {1;\,2; - 1} \right)//\,\,\left( {1;\,\,2; - 1} \right)\)
\( \Rightarrow \left( \alpha \right)\) nhận vecto \(\left( {1;\,2; - 1} \right)\) làm 1 VTPT.
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 1,\,\,{u_2} = - 2.\) Mệnh đề nào sau đây đúng?
-
A.
\({u_{2019}} = - {2^{2018}}\)
-
B.
\({u_{2019}} = {2^{2019}}\)
-
C.
\({u_{2019}} = - {2^{2019}}\)
-
D.
\({u_{2019}} = {2^{2018}}\)
Đáp án : D
Công thức tổng quát của CSN có số hạng đầu là \({u_1}\) và công bội \(q:\;{u_n} = {u_1}{q^{n - 1}}.\)
Gọi \(q\) là công bội của CSN đã cho, ta có: \({u_1} = 1;\,\,{u_2} = - 2 \Rightarrow q = \dfrac{{{u_2}}}{{{u_1}}} = \dfrac{{ - 2}}{1} = - 2.\)
\( \Rightarrow {u_{2019}} = {u_1}.{q^{2018}} = 1.{\left( { - 2} \right)^{2018}} = {2^{2018}}.\)
Hình dưới đây là đồ thị của hàm số nào?

-
A.
\(y = {x^2} - 2\)
-
B.
\(y = {x^4} + {x^2} - 2\)
-
C.
\(y = {x^4} - {x^2} - 2\)
-
D.
\(y = {x^2} + x - 2\)
Đáp án : B
Dựa vào đồ thị hàm số, nhận biết các điểm thuộc đồ thị hàm số và các điểm cực trị của đồ thị từ đó chọn đáp án đúng.
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có dạng là 1 parabol có đỉnh là \(\left( {0; - 2} \right) \Rightarrow \) loại đáp án A, D.
Đồ thị hàm số đi qua các điểm \(\left( {1;\,\,0} \right)\) và \(\left( { - 1;\,\,0} \right),\) thay tọa độ các điểm này vào công thức hàm số ở đáp án B và C thấy chỉ có đáp án B thỏa mãn.
có 1 điểm cực trị có tọa là \(\left( {0; - 2} \right)\)
Trong không gian \(Oxyz,\) cho điểm \(I\left( {1;\,\,2;\,\,5} \right)\) và mặt phẳng \(\left( \alpha \right):\,\,\,x - 2y + 2z + 2 = 0.\) Phương trình mặt cầu tâm \(I\) và tiếp xúc với \(\left( \alpha \right)\) là:
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 3\)
-
B.
\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 5} \right)^2} = 3\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 9\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 5} \right)^2} = 9\)
Đáp án : C
Phương trình mặt cầu tâm \(I\left( {a;\,b;\,c} \right)\) và bán kính \(R:\,\,{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}.\)
Gọi \(R\) là bán kính mặt cầu cần tìm \( \Rightarrow R = d\left( {I;\,\,\left( \alpha \right)} \right) = \dfrac{{\left| {1 - 2.2 + 2.5 + 2} \right|}}{{\sqrt {1 + {{\left( { - 2} \right)}^2} + {2^2}} }} = \dfrac{9}{3} = 3.\)
Vậy mặt cầu tâm \(I\) và tiếp xúc với \(\left( \alpha \right)\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 9.\)
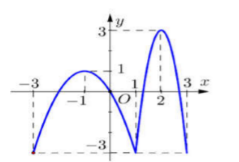
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.

Trên đoạn \(\left[ { - 3;\,3} \right],\) hàm số đã cho có mấy điểm cực trị?
-
A.
$4$
-
B.
$5$
-
C.
$2$
-
D.
$3$
Đáp án : D
Dựa vào đồ thị hàm số để nhận xét các điểm cực trị của hàm số.
Dựa vào đồ thị hàm số ta thầy, trên đoạn \(\left[ { - 3;\,\,3} \right],\) hàm số \(y = f\left( x \right)\) có 3 điểm cực trị là \(\left( { - 1;\,\,1} \right);\,\,\,\left( {1; - 3} \right);\,\,\left( {2;\,\,3} \right).\)
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục bất kì trên đoạn \(\left[ {a;\,\,b} \right].\) Mênh đề nào sau đây đúng?
-
A.
\(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
-
B.
\(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
-
C.
\(\left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} } \right|dx = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
-
D.
\(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \left| {\int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} } \right|\)
Đáp án : B
Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} .\)
Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} .\)
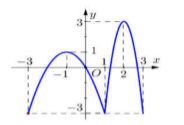
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng:

-
A.
\(\left( {0;\,\,2} \right)\)
-
B.
\(\left( { - 2;\,0} \right)\)
-
C.
\(\left( { - 3; - 1} \right)\)
-
D.
\(\left( {2;\,3} \right)\)
Đáp án : D
Dựa vào đồ thị hàm số để nhận xét các khoảng đồng biến và nghịch biến của hàm số.
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên các khoảng \(\left( { - 3;\, - 1} \right)\) và \(\left( {1;\,\,2} \right).\)
Hàm số nghịch biến trên các khoảng: \(\left( { - 1;\,1} \right)\) và \(\left( {2;\,\,3} \right).\)
Tất cả các nguyên hàm của hàm \(f\left( x \right) = \dfrac{1}{{\sqrt {3x - 2} }}\) là:
-
A.
\(2\sqrt {3x - 2} + C\)
-
B.
\(\dfrac{2}{3}\sqrt {3x - 2} + C\)
-
C.
\( - \dfrac{2}{3}\sqrt {3x - 2} + C\)
-
D.
\( - 2\sqrt {3x - 2} + C\)
Đáp án : B
Ta có: \(F\left( x \right) = \int {f\left( x \right)dx} \) thì \(F'\left( x \right) = f\left( x \right).\)
Đạo hàm các hàm số ở các đáp án rồi chọn đáp án đúng.
Ta có:
+) Đáp án A: \(\left( {2\sqrt {3x - 2} + C} \right)' = \dfrac{{2.3}}{{2\sqrt {3x - 2} }} = \dfrac{3}{{\sqrt {3x - 2} }} \ne \dfrac{1}{{\sqrt {3x - 2} }} \Rightarrow \) đáp án A sai.
+) Đáp án B: \(\left( {\dfrac{2}{3}\sqrt {3x - 2} + C} \right)' = \dfrac{{2.3}}{{3.2\sqrt {3x - 2} }} = \dfrac{1}{{\sqrt {3x - 2} }} \Rightarrow \) đáp án B đúng.
Khi đặt \({3^x} = t\) thì phương trình \({9^{x + 1}} - {3^{x + 1}} - 30 = 0\) trở thành:
-
A.
\(3{t^2} - t - 10 = 0\)
-
B.
\(9{t^2} - 3t - 10 = 0\)
-
C.
\({t^2} - t - 10 = 0\)
-
D.
\(2{t^2} - t - 1 = 0\)
Đáp án : A
Sử dụng công thức \({a^{m + n}} = {a^m}.{a^n}\) từ đó đặt ẩn phụ và chọn đáp án đúng.
Ta có: \({9^{x + 1}} - {3^{x + 1}} - 30 = 0 \Leftrightarrow {9.9^x} - {3.3^x} - 30 = 0 \Leftrightarrow 3.{\left( {{3^x}} \right)^2} - {3^x} - 10 = 0\,\,\,\left( * \right)\)
Đặt \({3^x} = t\) ta có phương trình \(\left( * \right) \Leftrightarrow 3{t^2} - t - 10 = 0.\)
Từ các chữ số \(1;\,\,2;\,\,3;\,\,......;\,\,9\) lập được bao nhiêu số có 3 chữ số đôi một khác nhau.
-
A.
\({3^9}\)
-
B.
\(A_9^3\)
-
C.
\({9^3}\)
-
D.
\(C_9^3\)
Đáp án : B
Chọn 3 số bất kì trong \(n\) số ta có: \(A_n^3\) cách chọn.
Cách 1: Gọi số cần tìm có dạng \(\overline {abc} \) là số cần lập.
Chọn 3 số \(a,\,\,b,\,\,c\) bất kì trong 9 số ta có: \(A_9^3\) cách chọn.
Cách 2: Gọi số cần tìm có dạng \(\overline {abc} \) là số cần lập.
Khi đó \(a\) có 9 cách chọn.
\(b \ne a \Rightarrow b\) có 8 cách chọn.
\(c \ne a,\,\,c \ne b \Rightarrow c\) có 7 cách chọn
\( \Rightarrow \) có \(9.8.7 = A_9^3 = 504\) cách chọn.
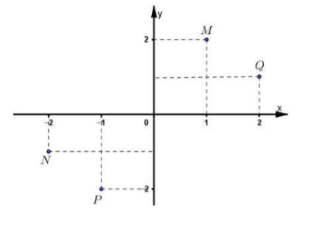
Cho số phức \(z = - 2 + i.\) Trong hình bên điểm biểu diễn số phức \(\overline z \) là:

-
A.
M
-
B.
Q
-
C.
P
-
D.
N
Đáp án : D
Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\)
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow M\left( {a;\,\,b} \right)\) là điểm biểu diễn số phức \(z.\)
Ta có: \(z = - 2 + i \Rightarrow \overline z = - 2 - i \Rightarrow N\left( { - 2; - 1} \right)\) là điểm biểu diễn số phức \(\overline z .\)
Trong không gian \(Oxyz,\) cho hai đường thẳng \({\Delta _1}:\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{{y + 2}}{1} = \dfrac{{z - 3}}{2}\) và \({\Delta _2}:\,\,\dfrac{{x + 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{{ - 4}}.\) Góc giữa hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) bằng:
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({135^0}\)
Đáp án : B
Cho hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) có các vecto chỉ phương lần lượt là: \(\overrightarrow {{u_1}} = \left( {{a_1};\,\,{b_1};\,\,{c_1}} \right)\) và \(\overrightarrow {{u_2}} = \left( {{a_2};\,\,{b_2};\,\,{c_2}} \right)\) thì góc giữa hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) được tính bằng công thức: \(\cos \alpha = \dfrac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \dfrac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\)
Ta có: \({\Delta _1}\) có VTCP là: \(\overrightarrow {{u_1}} = \left( { - 2;\,\,1;\,\,2} \right),\,\,\Delta \) có VTCP là: \(\overrightarrow {{u_2}} = \left( {1;\,\,1; - 4} \right).\)
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\left( {{\Delta _1};\,\,{\Delta _2}} \right)\) ta có:
\(\begin{array}{l}\cos \alpha = \dfrac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \dfrac{{\left| { - 2.1 + 1.1 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + 1 + {2^2}} .\sqrt {1 + 1 + {{\left( { - 4} \right)}^2}} }} = \dfrac{9}{{3.3\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.\\ \Rightarrow \alpha = {45^0}.\end{array}\)
Cho số phức \(z\) thỏa mãn \(z + 2\overline z = 6 + 2i.\) Điểm biểu diễn số phức \(z\) có tọa độ là:
-
A.
\(\left( {2; - 2} \right)\)
-
B.
\(\left( { - 2; - 2} \right)\)
-
C.
\(\left( {2;\,\,2} \right)\)
-
D.
\(\left( { - 2;\,\,2} \right)\)
Đáp án : A
Dựa vào biểu thức của đề bài để tìm số phức \(z.\)
Ta có:\({z_1} = {a_1} + {b_1}i;\,\,{z_2} = {a_2} + {b_2}i \Rightarrow {z_1} = {z_2} \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} = {b_2}\end{array} \right..\)
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow M\left( {a;\,\,b} \right)\) là điểm biểu diễn số phức \(z.\)
Gọi số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\) Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,z + 2\overline z = 6 + 2i \Leftrightarrow a + bi + 2\left( {a - bi} \right) = 6 + 2i\\ \Leftrightarrow 3a - bi = 6 + 2i \Leftrightarrow \left\{ \begin{array}{l}3a = 6\\ - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 2\end{array} \right. \Rightarrow z = 2 - 2i\end{array}\)
\( \Rightarrow M\left( {2; - 2} \right)\) là điểm biểu diễn số phức \(z.\)
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\,\,\dfrac{{x - 2}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{z}{2}\) và mặt phẳng \(\left( P \right):\,\,x + 2y - z - 5 = 0.\) Tọa độ giao điểm của \(d\) và \(\left( P \right)\) là:
-
A.
\(\left( {2;\,\,1; - 1} \right)\)
-
B.
\(\left( {3; - 1; - 2} \right)\)
-
C.
\(\left( {1;\,\,3; - 2} \right)\)
-
D.
\(\left( {1;\,\,3;\,\,2} \right)\)
Đáp án : D
Ta có: \(d:\,\,\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c} \Rightarrow d:\,\,\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right. \Rightarrow M\left( {{x_0} + at;\,\,{y_0} + bt;\,\,{z_0} + ct} \right)\) là một điểm thuộc đường thẳng \(d.\)
\(M = d \cap \left( P \right) \Rightarrow \) tọa độ điểm \(M\) thỏa mãn phương trình mặt phẳng \(\left( P \right).\) Từ đó tìm được \(t \Rightarrow \) tọa độ điểm \(M.\)
Ta có: \(d:\,\,\dfrac{{x - 2}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{z}{2} \Rightarrow d:\,\,\,\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 2t\end{array} \right. \Rightarrow M\left( {2 - t;\,1 + 2t;\,2t} \right)\) là một điểm thuộc đường thẳng \(d.\)
\(\begin{array}{l}M = d \cap \left( P \right) \Rightarrow 2 - t + 2\left( {1 + 2t} \right) - \left( {2t} \right) - 5 = 0\\ \Leftrightarrow t = 1 \Rightarrow M\left( {1;\,\,3;\,\,2} \right).\end{array}\)
Bất phương trình \({\log _4}\left( {{x^2} - 3x} \right) > {\log _2}\left( {9 - x} \right)\) có bao nhiêu nghiệm nguyên?
-
A.
vô số
-
B.
$1$
-
C.
$4$
-
D.
$3$
Đáp án : D
+) Tìm điều kiện xác định.
+) Giải bất phương trình logarit: \({\log _a}f\left( x \right) > {\log _a}g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a > 1\\f\left( x \right) > g\left( x \right)\end{array} \right.\\\left\{ \begin{array}{l}0 < a < 1\\f\left( x \right) < g\left( x \right)\end{array} \right.\end{array} \right..\)
Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 3x > 0\\9 - x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x\left( {x - 3} \right) > 0\\x < 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x > 3\\x < 0\end{array} \right.\\x < 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x < 0\\3 < x < 9\end{array} \right..\)
\(\begin{array}{l}{\log _4}\left( {{x^2} - 3x} \right) > {\log _2}\left( {9 - x} \right) \Leftrightarrow \dfrac{1}{2}{\log _2}\left( {{x^2} - 3x} \right) > {\log _2}\left( {9 - x} \right)\\ \Leftrightarrow {\log _2}\left( {{x^2} - 3x} \right) > 2{\log _2}\left( {9 - x} \right) \Leftrightarrow {\log _2}\left( {{x^2} - 3x} \right) > {\log _2}{\left( {9 - x} \right)^2}\\ \Leftrightarrow {x^2} - 3x > 81 - 18x + {x^2}\\ \Leftrightarrow 15x > 81 \Leftrightarrow x > \dfrac{{81}}{{15}} \Leftrightarrow x > \dfrac{{27}}{5}\end{array}\)
Kết hợp với điều kiện xác định ta có bất phương trình có tập nghiệm là: \(\dfrac{{27}}{5} < x < 9.\)
Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ {6;\,\,7;\,\,8} \right\}.\)
Hàm số \(y = {\left( {{x^3} - 3x} \right)^e}\) có bao nhiêu điểm cực trị?
-
A.
$2$
-
B.
$0$
-
C.
$3$
-
D.
$1$
Đáp án : D
Ta có: \(x = {x_0}\) là điểm cực trị của hàm số \(y = f\left( x \right) \Rightarrow f'\left( {{x_0}} \right) = 0.\)
Điều kiện: \({x^3} - 3x > 0 \Leftrightarrow x\left( {{x^2} - 3} \right) > 0 \Leftrightarrow x\left( {x - \sqrt 3 } \right)\left( {x + \sqrt 3 } \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - \sqrt 3 < x < 0\\x > \sqrt 3 \end{array} \right..\)
Ta có: \(y' = e\left( {3{x^2} - 3} \right){\left( {{x^3} - 3x} \right)^{e - 1}}.\)
\( \Rightarrow y' = 0 \Leftrightarrow \left( {3{x^2} - 3} \right){\left( {{x^3} - 3x} \right)^{e - 1}} = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right.\)
Ta có bảng xét dấu:
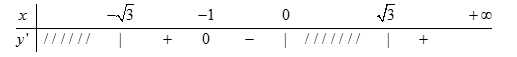
Dựa vào bảng xét dấu của hàm số ta thấy đạo hàm của hàm số chỉ đổi dấu qua 1 điểm \(x = - 1 \Rightarrow \) hàm số có 1 điểm cực trị.
Gọi \(\left( D \right)\) là hình phẳng giới hạn bởi các đường \(y = {2^x},\,\,y = 0,\,\,x = 0\) và \(x = 2.\) Thể tích \(V\) của khối tròn xoay tạo thành khi quay \(\left( D \right)\) quanh trục \(Ox\) được xác định bởi công thức:
-
A.
\(V = \pi \int\limits_0^2 {{2^{x + 1}}dx} \)
-
B.
\(V = \int\limits_0^2 {{2^{x + 1}}dx} \)
-
C.
\(V = \int\limits_0^2 {{4^x}dx} \)
-
D.
\(V = \pi \int\limits_0^2 {{4^x}dx} \)
Đáp án : D
Công thức tính thể tích hình phẳng được giới hạn bởi các đường thẳng \(x = a,\;x = b\;\;\left( {a < b} \right)\) và các đồ thị hàm số \(y = f\left( x \right),\;y = g\left( x \right)\) khi quay quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx.} \)
Ta có công thức tính thể tích hình phẳng đã cho là: \(V = \pi \int\limits_0^2 {{{\left( {{2^x}} \right)}^2}dx} = \pi \int\limits_0^2 {{4^x}dx} \)
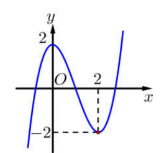
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Đáp án : A
Dựa vào đồ thị hàm số suy ra các khoảng đồng biến và nghịch biến của hàm số \(y = f\left( x \right)\) từ đó suy ra tính đồng biến và nghịch biến của hàm số \(y = - 2f\left( x \right)\).
Dựa vào đồ thị hàm số ta có \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;2} \right)\), suy ra f'(x) < 0 trên khoảng (0;2).
Xét hàm số: \(y = - 2f\left( x \right)\) ta có: \(y' = - 2f'\left( x \right)\).
Hàm số \(y = - 2f\left( x \right)\) đồng biến khi \(y' > 0 \Leftrightarrow - 2f'\left( x \right) > 0 \Leftrightarrow f'\left( x \right) < 0 \Leftrightarrow 0 < x < 2\).
Vậy hàm số \(y = - 2f\left( x \right)\) đồng biến \( \Leftrightarrow x \in \left( {0;2} \right)\).
Xét các đáp án thấy chỉ có khoảng (1;2) thuộc (0;2) nên đáp án A đúng.
Đồ thị hàm số \(y = \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}}\) có bao nhiêu đường tiệm cận?
-
A.
$4$
-
B.
$3$
-
C.
$1$
-
D.
$2$
Đáp án : B
+) Đường thẳng \(x = a\) được gọi là TCĐ của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \infty \).
+) Đường thẳng \(y = b\) được gọi là TCN của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b.\)
Điều kiện: \(x \ne 1.\)
\( \Rightarrow x = 1\) là đường TCĐ của đồ thị hàm số.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 + \sqrt {1 + \dfrac{1}{{{x^2}}}} }}{{1 - \dfrac{1}{x}}} = 2\)
\( \Rightarrow y = 2\) là 1 đường TCN của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \sqrt {1 + \dfrac{1}{{{x^2}}}} }}{{1 - \dfrac{1}{x}}} = 0\)
\( \Rightarrow y = 0\) là 1 đường TCN của đồ thị hàm số.
Vậy đồ thị hám số đã cho có 2 TCN và 1 TCĐ.
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:

-
A.
\(\dfrac{1}{2}\)
-
B.
\(\sqrt 3 \)
-
C.
\(2\)
-
D.
\(\sqrt[3]{2}\)
Đáp án : D
Dựa vào đồ thị hàm số, xác định các giá trị của \({x_1},\,{x_2}\) theo \(a\) và \(b.\) Từ đó tính giá trị của \(\dfrac{a}{b}.\)
Dựa vào đồ thị hàm số ta thấy \({x_1}\) là nghiệm của phương trình hoành độ giao điểm \({\log _b}{x_1} = 3 \Leftrightarrow {x_1} = {b^3}.\)
Và \({x_2}\) là nghiệm của phương trình hoành độ giao điểm \({\log _a}{x_2} = 3 \Leftrightarrow {x_2} = {a^3}.\)
Theo đề bài ta có: \({x_2} = 2{x_1} \Rightarrow {a^3} = 2{b^3} \Leftrightarrow \dfrac{{{a^3}}}{{{b^3}}} = 2 \Leftrightarrow \dfrac{a}{b} = \sqrt[3]{2}.\)
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,\,\,AD = 2a,\,AC' = \sqrt 6 a.\) Thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) bằng:
-
A.
\(\dfrac{{\sqrt 3 {a^3}}}{3}\)
-
B.
\(\dfrac{{2{a^3}}}{3}\)
-
C.
\(2{a^3}\)
-
D.
\(2\sqrt 3 {a^3}\)
Đáp án : C
Công thức tính thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) là: \(V = AA'.AB.AD.\)
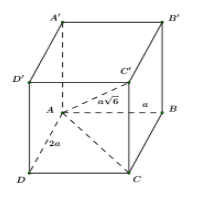
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \) (định lý Pitago)
Xét tam giác \(ACC'\) vuông tại \(C\) ta có:
\(\begin{array}{l}CC' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {6{a^2} - 5{a^2}} = a.\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = CC'.AB.AD = a.a.2a = 2{a^3}.\end{array}\)
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} + x} \right){\left( {x - 2} \right)^2}\left( {{2^x} - 4} \right),\,\,\,\forall x \in \mathbb{R}.\) Số điểm cực trị của \(f\left( x \right)\) là:
-
A.
$2$
-
B.
$4$
-
C.
$3$
-
D.
$1$
Đáp án : C
Số điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\) là số nghiệm bội lẻ của phương trình \(f'\left( x \right) = 0.\)
Ta có: \(f'\left( x \right) = 0\)
\(\begin{array}{l} \Leftrightarrow \left( {{x^2} + x} \right){\left( {x - 2} \right)^2}\left( {{2^x} - 4} \right) = 0\\ \Leftrightarrow x\left( {x + 1} \right){\left( {x - 2} \right)^2}\left( {{2^x} - {2^2}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x + 1 = 0\\x - 2 = 0\\{2^x} - {2^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\\x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,\left( {bội\,\,1} \right)\\x = - 1\,\,\,\,\,\left( {bội\,\,1} \right)\\x = 2\,\,\,\,\,\left( {bội\,\,\,3} \right)\end{array} \right..\end{array}\)
Ta thầy phương trình \(f'\left( x \right) = 0\) có 3 nghiệm phân biệt và các nghiệm này đều là nghiệm bội lẻ nên hàm số \(y = f\left( x \right)\) có 3 điểm cực trị.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Diện tích xung quanh của hình trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông \(ABCD\) và \(A'B'C'D'\) là:
-
A.
\(\sqrt 2 \pi {a^2}\)
-
B.
\(2\pi {a^2}\)
-
C.
\(\pi {a^2}\)
-
D.
\(2\sqrt 2 \pi {a^2}\)
Đáp án : A
Công thức tính diện tích xung quanh hình trụ có bán kính đáy \(R,\;\)chiều cao \(h:\;\;{S_{xq}} = 2\pi Rh.\)
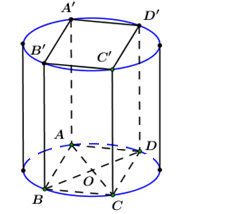
Ta có hình hộp \(ABCD.A'B'C'D'\) có các cạnh bằng \(a\)
\( \Rightarrow AA' = a\) là đường sinh của hình trụ.
Bán kính đáy của hình trụ là \(R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}.\)
\( \Rightarrow \) Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi Rl = 2\pi .\dfrac{{a\sqrt 2 }}{2}.a = \sqrt 2 \pi {a^2}.\)
Gọi \({z_1},\,\,{z_2}\) là các nghiệm phức của phương trình \({z^2} - 2z + 3 = 0.\) Modul của \(z_1^3.z_2^4\) bằng:
-
A.
\(81\)
-
B.
\(16\)
-
C.
\(27\sqrt 3 \)
-
D.
\(8\sqrt 2 \)
Đáp án : C
Giải phương trình đã cho tìm hai số phức \({z_1},\,\,{z_2}\) rồi tính modul của số phức đề bài yêu cầu.
Ta có: \({z^2} - 2z + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 1 + \sqrt 2 i \Rightarrow \left| {{z_1}} \right| = \sqrt {1 + 2} = \sqrt 3 \\{z_2} = 1 - \sqrt 2 i \Rightarrow \left| {{z_2}} \right| = \sqrt {1 + 2} = \sqrt 3 \end{array} \right..\)
\( \Rightarrow \left| {z_1^3.z_2^4} \right| = {\left| {{z_1}} \right|^3}.{\left| {{z_2}} \right|^4} = {\left( {\sqrt 3 } \right)^3}.{\left( {\sqrt 3 } \right)^4} = {\left( {\sqrt 3 } \right)^7} = 27\sqrt 3 .\)
Gọi \(m,\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2}\) trên đoạn \(\left[ { - 2;\,\,2} \right].\) Giá trị của \(m + M\) bằng:
-
A.
\(2\)
-
B.
\( - 2\)
-
C.
\(0\)
-
D.
\( - 4\)
Đáp án : B
Cách 1:
+) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách:
+) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\)
+) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó:
\(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\)
Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\)
Ta có: \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2} \Rightarrow f'\left( x \right) = 2 - \dfrac{\pi }{2}\sin \dfrac{{\pi x}}{2}.\)
Vì \( - 1 \le \sin \dfrac{{\pi x}}{2} \le 1 \Rightarrow - \dfrac{\pi }{2} \le \dfrac{\pi }{2}\sin \dfrac{{\pi x}}{2} \le \dfrac{\pi }{2} \Rightarrow 0 < 2 - \dfrac{\pi }{2} \le 2 - \dfrac{\pi }{2}\sin \dfrac{{\pi x}}{2} \le 2 + \dfrac{\pi }{2}\)
\( \Rightarrow f'\left( x \right) > 0\,\,\forall x \in \left[ { - 2;\,\,2} \right] \Rightarrow \) hàm số \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2}\) là hàm đồng biến trên \(\left[ { - 2;\,\,2} \right].\)
\(\begin{array}{l} \Rightarrow f\left( { - 2} \right) \le f\left( x \right) \le f\left( 2 \right)\,\,\,\forall x \in \left[ { - 2;\,\,2} \right].\\ \Rightarrow \left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 2;\,\,2} \right]} f\left( x \right) = f\left( 2 \right) = 3\\m = \mathop {\min }\limits_{\left[ { - 2;\,\,2} \right]} f\left( x \right) = f\left( { - 2} \right) = - 5\end{array} \right.\\ \Rightarrow M + m = 3 + \left( { - 5} \right) = - 2.\end{array}\)
Cho hình chóp đều \(SABCD\) có \(AB = 2a,\,\,SA = a\sqrt 5 .\) Góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng:
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({75^0}\)
Đáp án : C
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng thuộc hai mặt phẳng cùng vuông góc với giao tuyến của hai mặt phẳng.
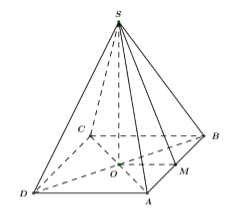
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
\(SABCD\) là hình chóp đều \( \Rightarrow SO \bot \left( {ABCD} \right).\)
Ta có: \(\left( {SAB} \right) \cap \left( {ABCD} \right) = \left\{ {AB} \right\}.\)
Gọi \(M\) là trung điểm của \(AB.\)
Ta có:\(OM \bot AB\,\,\left( {OM//AD,\,\,AD \bot AB} \right)\)
\(SM \bot AB\) do \(\Delta SAB\) là tam giác cân tại \(S.\)
\( \Rightarrow \angle \left( {\left( {SAB} \right),\,\,\left( {ABCD} \right)} \right) = \angle \left( {SM,\,\,OM} \right) = \angle SMO.\)
Ta có: \(SM = \sqrt {S{A^2} - M{A^2}} = \sqrt {5{a^2} - {a^2}} = 2a.\) (Định lý Pitago)
\(OM = \dfrac{1}{2}AD = a.\)
\(\begin{array}{l} \Rightarrow \cos SMO = \dfrac{{OM}}{{SM}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\\ \Rightarrow \angle SMO = {60^0}.\end{array}\)
Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng:
-
A.
\(\dfrac{{145}}{{729}}\)
-
B.
\(\dfrac{{448}}{{729}}\)
-
C.
\(\dfrac{{281}}{{729}}\)
-
D.
\(\dfrac{{154}}{{729}}\)
Đáp án : C
- Liệt kê các trường hợp có lợi cho biến cố và đếm số khả năng xảy ra.
- Tính xác suất và kết luận.
Số các số tự nhiên có 2 chữ số phân biệt là \(9.9 = 81 \Rightarrow n\left( \Omega \right) = {81^2}\).
Gọi A là biến cố: “ Hai số được viết ra có ít nhất một chữ số chung”
TH1: Hai bạn cùng viết hai số giống nhau \( \Rightarrow \) Có 81 cách.
TH2: Bạn Công viết số có dạng \(\overline {ab} \) và bạn Thành viết số có dạng \(\overline {ba} \).
\( \Rightarrow a \ne b \ne 0 \Rightarrow \) Có \(9.8 = 72\) cách.
TH3: Hai bạn chọn số chỉ có 1 chữ số trùng nhau.
+) Trùng số 0: Số cần viết có dạng \(\overline {a0} \), Công có 9 cách viết, Thành có 8 cách viết (Khác số Công viết)
\( \Rightarrow \) Có \(9.8 = 72\) cách.
+) Trùng số 1: Số cần viết có dạng \(\overline {a1} \,\,\left( {a \ne 0,\,\,a \ne 1} \right)\), hoặc \(\overline {1b} \,\,\left( {b \ne 1} \right)\).
Nếu Công viết số 10 , khi đó Thành có 8 cách viết số có dạng \(\overline {a1} \,\,\left( {a \ne 0,\,\,a \ne 1} \right)\) và 8 cách viết số có dạng \(\overline {1b} \,\,\left( {b \ne 1} \right)\) \( \Rightarrow \) Có 16 cách.
Nếu Công viết số có dạng \(\overline {1b} \,\,\left( {b \ne 0,\,\,b \ne 1} \right)\) \( \Rightarrow \) Công có 8 cách viết, khi đó Thành có 7 cách viết số có dạng \(\overline {a1} \,\,\left( {a \ne 0,\,\,a \ne 1} \right)\) và 8 cách viết số có dạng \(\overline {1b} \,\,\left( {b \ne 1} \right)\).
\( \Rightarrow \) Có \(8\left( {7 + 8} \right) = 120\) cách.
Nếu Công viết có dạng \(\overline {a1} \,\,\left( {a \ne 0,\,\,a \ne 1} \right)\) \( \Rightarrow \) Công có 8 cách viết, khi đó Thành có 7 cách viết số có dạng \(\overline {a1} \,\,\left( {a \ne 0,\,\,a \ne 1} \right)\) và 8 cách viết số có dạng \(\overline {1b} \,\,\left( {b \ne 1} \right)\).
\( \Rightarrow \) Có \(8\left( {7 + 8} \right) = 120\) cách.
\( \Rightarrow \) Có 256 cách viết trùng số 1.
Tương tự cho các trường hợp trùng số 2,3,4,5,6,7,8,9.
\( \Rightarrow n\left( A \right) = 81 + 72 + 72 + 256.9 = 2529\).
Vậy \(P\left( A \right) = \dfrac{{2529}}{{{{81}^2}}} = \dfrac{{281}}{{729}}\).
Biết rằng \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) trên khoảng \(\left( { - \infty ; + \infty } \right)\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f'\left( x \right){e^x}\) thỏa mãn \(F\left( 0 \right) = 1\), giá trị của \(F\left( { - 1} \right)\) bằng:
-
A.
\(\dfrac{7}{2}\)
-
B.
\(\dfrac{{5 - e}}{2}\)
-
C.
\(\dfrac{{7 - e}}{2}\)
-
D.
\(\dfrac{5}{2}\)
Đáp án : A
+) \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) nên \(\left( {x{e^x}} \right)' = f\left( { - x} \right)\).
+) Từ \(f\left( { - x} \right) \Rightarrow f\left( x \right)\).
+) \(F\left( x \right)\) là một nguyên hàm của \(f'\left( x \right){e^x} \Rightarrow F\left( x \right) = \int\limits_{}^{} {f'\left( x \right){e^x}dx} \).
+) Tính \(F\left( x \right),\) từ đó tính \(F\left( { - 1} \right)\).
Vì \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) nên \(\left( {x{e^x}} \right)' = f\left( { - x} \right) \Leftrightarrow f\left( { - x} \right) = {e^x} + x{e^x} = {e^x}\left( {1 + x} \right)\).
\( \Rightarrow f\left( x \right) = {e^{ - x}}\left( {1 - x} \right)\).
\(\begin{array}{l} \Rightarrow f'\left( x \right) = - {e^{ - x}}\left( {1 - x} \right) - {e^{ - x}} = - {e^{ - x}}\left( {2 - x} \right) = \left( {x - 2} \right){e^{ - x}}\\ \Rightarrow f'\left( x \right){e^x} = \left( {x - 2} \right){e^{ - x}}.{e^x} = x - 2\\ \Rightarrow F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {\left( {x - 2} \right)dx} = \dfrac{{{x^2}}}{2} - 2x + C\\F\left( 0 \right) = 1 \Rightarrow C = 1 \Rightarrow F\left( x \right) = \dfrac{{{x^2}}}{2} - 2x + 1\\ \Rightarrow F\left( { - 1} \right) = \dfrac{{{{\left( { - 1} \right)}^2}}}{2} - 2\left( { - 1} \right) + 1 = \dfrac{7}{2}\end{array}\)
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(AB = 2a,\,\,AD = a,\,\,SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\). Khoảng cách giữa hai đường thẳng \(SC\) và \(BM\) bằng:
-
A.
\(\dfrac{{3\sqrt 3 a}}{4}\)
-
B.
\(\dfrac{{2\sqrt 3 a}}{3}\)
-
C.
\(\dfrac{{\sqrt 3 a}}{3}\)
-
D.
\(\dfrac{{\sqrt 3 a}}{2}\)
Đáp án : B
Dựng mặt phẳng \((\alpha )\) chứa \(BM\) và song song \(SC\).
Khi đó $d\left( {BM,SC} \right) = d\left( {SC,\left( \alpha \right)} \right)$
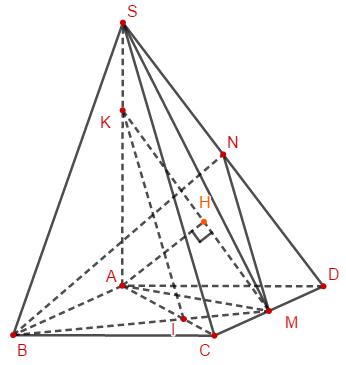
Gọi I là giao điểm của MB và AC, kẻ \(IK//SC\left( {K \in SA} \right)\), kẻ \(MN//SC\left( {N \in S{\rm{D}}} \right)\). Khi đó \(KI,MN \subset \left( {BMN} \right)\). Kẻ \(AH \bot KM\)
Do ABCD là hình chữ nhật có AB=2CD nên \(AM \bot BM \Rightarrow BM \bot \left( {SAM} \right)\)
\( \Rightarrow \left( {BMN} \right) \bot \left( {SAM} \right) \Rightarrow AH \bot \left( {BMN} \right)\)
Ta có AI=2CI (vì CM//AB và AB=2CM)
Suy ra AK=2KS và
\(\begin{array}{l}d\left( {SC,BM} \right) = d\left( {SC,\left( {BMN} \right)} \right) = d\left( {C,\left( {BMN} \right)} \right)\\ = \dfrac{1}{2}d\left( {A,\left( {BMN} \right)} \right) = \dfrac{1}{2}AH\end{array}\)
\(\begin{array}{l}AK = \dfrac{2}{3}SA = 2{\rm{a}};AM = AD\sqrt 2 = a\sqrt 2 \\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{K^2}}} + \dfrac{1}{{A{M^2}}} = \dfrac{1}{{4{{\rm{a}}^2}}} + \dfrac{1}{{2{{\rm{a}}^2}}} = \dfrac{3}{{4{{\rm{a}}^2}}}\\ \Rightarrow AH = \dfrac{{2a\sqrt 3 }}{3}\end{array}\)
Đối với lớp 12 có thể sử dụng phương pháp tọa độ như sau:
Đặt hệ trục toa độ như hình vẽ, chọn \(a = 1\). Khi đó ta có:
\(A\left( {0;0;0} \right),\,\,B\left( {2;0;0} \right),\,\,C\left( {2;1;0} \right);\,\,D\left( {0;1;0} \right);\,\,S\left( {0;0;3} \right)\)
\(M\) là trung điểm cạnh \(CD \Rightarrow M\left( {1;1;0} \right)\).
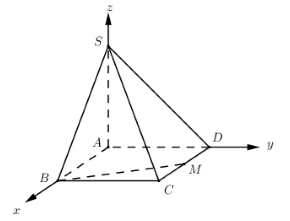
Ta có \(\overrightarrow {SC} = \left( { - 2; - 1;3} \right);\,\,\overrightarrow {BM} = \left( { - 1;1;0} \right);\,\,\overrightarrow {SB} = \left( {2;0; - 3} \right)\) \( \Rightarrow \left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right] = \left( { - 3; - 3; - 3} \right)\).
\( \Rightarrow d\left( {SC;BM} \right) = \dfrac{{\left| {\left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right].\overrightarrow {SB} } \right|}}{{\left| {\left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right]} \right|}} = \dfrac{{\left| { - 3.2 - 3.0 + \left( { - 3} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2}} }} = \dfrac{3}{{3\sqrt 3 }} = \dfrac{{\sqrt 3 }}{3}\)
Cho hàm số \(f\left( x \right)\) có bảng xét dấu có đạo hàm như hình bên dưới
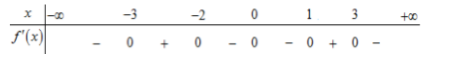
Hàm số \(y = f\left( {1 - 2x} \right)\) đồng biến trên khoảng
-
A.
\(\left( {0;\dfrac{3}{2}} \right)\)
-
B.
\(\left( { - \dfrac{1}{2};1} \right)\)
-
C.
\(\left( { - 2; - \dfrac{1}{2}} \right)\)
-
D.
\(\left( {\dfrac{3}{2};3} \right)\)
Đáp án : A
Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {a;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.
Ta có: \(y' = - 2f'\left( {1 - 2x} \right)\).
Với \(x = 1 \Rightarrow y'\left( 1 \right) = - 2f'\left( { - 1} \right) > 0 \Rightarrow \) Loại đáp án B, C, D.
Ngoài phương pháp thử HS có thể lập BXD \(y'\), tuy nhiên trong bài tập này, thử là phương pháp tối ưu nhất.
Cách tự luận:
\(\begin{array}{l}y' > 0 \Leftrightarrow - 2f'\left( {1 - 2x} \right) > 0\\ \Leftrightarrow f'\left( {1 - 2x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}1 - 2x < - 3\\ - 2 < 1 - 2x < 0\\0 < 1 - 2x < 1\\1 - 2x > 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\frac{1}{2} < x < \frac{3}{2}\\0 < x < \frac{1}{2}\\x < - 1\end{array} \right.\end{array}\)
Nên hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {0;\frac{3}{2}} \right),\left( {2; + \infty } \right)\)
(trong khoảng \(\left( {0;\frac{3}{2}} \right)\) chứa điểm \(x = \frac{1}{2}\) làm cho đạo hàm \(f'\left( {1 - 2x} \right) = 0\) vẫn được)
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| {w - i} \right| = 2,\,\,z + 2 = iw\). Gọi \({z_1},\,\,{z_2}\) lần lượt là các số phức mà tại đó \(\left| z \right|\) đạt giá trị nhỏ nhất và giá trị lớn nhất. Môđun \(\left| {{z_1} + {z_2}} \right|\) bằng:
-
A.
\(3\sqrt 2 \)
-
B.
\(3\)
-
C.
\(6\)
-
D.
\(6\sqrt 2 \)
Đáp án : C
Sử dụng phương pháp hình học.
Theo bài ra ta có:
\(\begin{array}{l}z + 2 = iw \Rightarrow w = \dfrac{{z + 2}}{i}\\\left| {w - i} \right| = 2 \Rightarrow \left| {\dfrac{{z + 2}}{i} - i} \right| = 2 \Leftrightarrow \left| {z + 2 + 1} \right| = 2 \Leftrightarrow \left| {z + 3} \right| = 2\end{array}\)
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \(I\left( { - 3;0} \right)\) bán kính \(R = 2\).
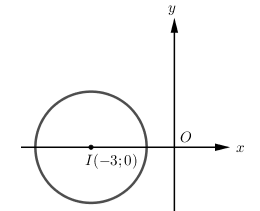
Gọi \(M\) là điểm biểu diễn số phức \(z\), dựa vào hình vẽ ta có:
\(\left\{ \begin{array}{l}{\left| z \right|_{\min }} \Leftrightarrow O{M_{\min }} \Leftrightarrow M\left( { - 1;0} \right) \Rightarrow {z_1} = - 1\\{\left| z \right|_{\max }} \Leftrightarrow O{M_{\max }} \Leftrightarrow M\left( { - 5;0} \right) \Rightarrow {z_2} = - 5\end{array} \right. \Rightarrow \left| {{z_1} + {z_2}} \right| = 6\).
Cho \(f\left( x \right) = {\left( {x - 1} \right)^3} - 3x + 3\). Đồ thị hình bên là của hàm số có công thức:

-
A.
\(y = - f\left( {x + 1} \right) - 1\)
-
B.
\(y = - f\left( {x + 1} \right) + 1\)
-
C.
\(y = - f\left( {x - 1} \right) - 1\)
-
D.
\(y = - f\left( {x - 1} \right) + 1\)
Đáp án : B
Xác định các hàm số ở các đáp án, thử điểm mà đồ thị hàm số đi qua để loại đáp án.
Đáp án A: \(y = - f\left( {x + 1} \right) - 1 = - {x^3} - 3\left( {x + 1} \right) + 3 - 1 = - {x^3} - 3x - 1\). Đồ thị hàm số đi qua điểm \(\left( {0; - 1} \right) \Rightarrow \) Loại.
Đáp án B: \(y = - f\left( {x + 1} \right) + 1 = - {x^3} - 3\left( {x + 1} \right) + 3 + 1 = - {x^3} + 3x + 1\). Đồ thị hàm số đi qua điểm \(\left( {0;1} \right) \Rightarrow \) Đáp án B có thể đúng.
Đáp án C: \(y = - {\left( {x - 2} \right)^3} - 3\left( {x - 1} \right) - 1 = - {x^3} + 6{x^2} - 15x + 10 = 0\). Đồ thị hàm số đi qua điểm \(\left( {0;10} \right) \Rightarrow \) Loại.
Đáp án D: \(y = - {\left( {x - 2} \right)^3} - 3\left( {x - 1} \right) + 1 = - {x^3} + 6{x^2} - 15x + 12 = 0\). Đồ thị hàm số đi qua điểm \(\left( {0;12} \right) \Rightarrow \) Loại.
Người ta xếp hai quả cầu có cùng bán kính \(r\) vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là \(120\,\,c{m^3}\), thể tích của mỗi khối cầu bằng

-
A.
\(10\,\,c{m^3}\)
-
B.
\(20\,\,c{m^3}\)
-
C.
\(30\,\,c{m^3}\)
-
D.
\(40\,\,c{m^3}\)
Đáp án : B
Thể tích khối cầu có bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\).
Thể tích khôi trụ có bán kính \(R\), chiều cao \(h\) là \(V = \pi {R^2}h\).
Dựa vào dữ kiện bài toán và hình vẽ \( \Rightarrow \) Hình trụ có chiều cao \(h = 2r\) và bán kính đáy \(R = 2r\).
\( \Rightarrow \) Thể tích khối trụ là \(V = \pi {\left( {2r} \right)^2}2r = 8\pi {r^3} = 120 \Leftrightarrow {r^3} = \dfrac{{120}}{{8\pi }} = \dfrac{{15}}{\pi }\).
Vậy thể tích mỗi khối cầu là \({V_c} = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi .\dfrac{{15}}{\pi } = 20\,\,\left( {c{m^3}} \right)\).
Biết \(\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{{{\cos }^2}x + \sin x\cos x + 1}}{{{{\cos }^4}x + \sin x{{\cos }^3}x}}dx} = a + b\ln 2 + c\ln \left( {1 + \sqrt 3 } \right)\), với \(a,\,\,b,\,\,c\) là các số hữu tỉ. Giá trị của \(abc\) bằng:
-
A.
\(0\)
-
B.
\( - 2\)
-
C.
\( - 4\)
-
D.
\( - 6\)
Đáp án : C
Chia cả tử và mẫu của phân thức trong dấu tích phân cho \({\cos ^2}x\) sau đó sử dụng phương pháp đổi biến, đặt \(t = \tan x\).
\(I = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{{{\cos }^2}x + \sin x\cos x + 1}}{{{{\cos }^4}x + \sin x{{\cos }^3}x}}dx} = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{1 + \tan x + 1 + {{\tan }^2}x}}{{{{\cos }^2}x\left( {1 + \tan x} \right)}}dx} = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{{{\tan }^2}x + \tan x + 2}}{{{{\cos }^2}x\left( {1 + \tan x} \right)}}dx} \)
Đặt \(t = \tan x \Rightarrow dt = \dfrac{1}{{{{\cos }^2}x}}dx\). Đổi cận \(\left\{ \begin{array}{l}x = \dfrac{\pi }{4} \Rightarrow t = 1\\x = \dfrac{\pi }{3} \Rightarrow t = \sqrt 3 \end{array} \right.\).
\(\begin{array}{l} \Rightarrow I = \int\limits_1^{\sqrt 3 } {\dfrac{{{t^2} + t + 2}}{{t + 1}}dt} = \int\limits_1^{\sqrt 3 } {\left( {t + \dfrac{2}{{t + 1}}} \right)dt} \\ = \left. {\dfrac{{{t^2}}}{2} + 2\ln \left| {t + 1} \right|} \right|_1^{\sqrt 3 } = \dfrac{3}{2} + 2\ln \left( {\sqrt 3 + 1} \right) - \dfrac{1}{2} - 2\ln 2 = 1 - 2\ln 2 + 2\ln \left( {1 + \sqrt 3 } \right)\\ \Rightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\\c = 2\end{array} \right. \Rightarrow abc = 1.\left( { - 2} \right).2 = - 4\end{array}\)
Trong không gian \(Oxyz\), cho hai đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = - 1 - 2t\\y = t\\z = - 1 + 3t\end{array} \right.,\,\,d':\,\,\left\{ \begin{array}{l}x = 2 + t'\\y = - 1 + 2t'\\z = - 2t'\end{array} \right.\) và mặt phẳng \(\left( P \right):\,\,x + y + z + 2 = 0\). Đường thẳng vuông góc với mặt phẳng \(\left( P \right)\) và cắt hai đường thẳng \(d,\,\,d'\) có phương trình là:
-
A.
\(\dfrac{{x - 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{1}\)
-
B.
\(\dfrac{{x - 1}}{1} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{{z - 1}}{{ - 4}}\)
-
C.
\(\dfrac{{x + 2}}{1} = \dfrac{{y + 1}}{1} = \dfrac{{z - 1}}{1}\)
-
D.
\(\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{2} = \dfrac{{z - 4}}{2}\)
Đáp án : A
+) Gọi \(\Delta \) là đường thẳng cần tìm.
+) Giả sử \(A = \Delta \cap d \Rightarrow A\left( { - 1 - 2t;t; - 1 + 3t} \right)\); \(B = \Delta \cap d' \Rightarrow B\left( {2 + t'; - 1 + 2t'; - 2t'} \right)\) \( \Rightarrow \overrightarrow {AB} \) là 1 VTCP của \(\Delta \)
+) \(\left( P \right)\) nhận \(\overrightarrow n \left( {1;1;1} \right)\) là 1 VTPT. Do \(\Delta \bot \left( P \right) \Rightarrow \overrightarrow {AB} \) và \(\overrightarrow n \) là 2 vectơ cùng phương. Tìm \(t,t'\).
+) Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) là có 1 VTCP \(\overrightarrow u \left( {a;b;c} \right)\): \(\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\).
Gọi \(\Delta \) là đường thẳng cần tìm.
Giả sử \(A = \Delta \cap d \Rightarrow A\left( { - 1 - 2t;t; - 1 + 3t} \right)\).
\(B = \Delta \cap d' \Rightarrow B\left( {2 + t'; - 1 + 2t'; - 2t'} \right)\).
\( \Rightarrow \overrightarrow {AB} = \left( {2t + t' + 3; - t + 2t' - 1; - 3t - 2t' + 1} \right)\) là 1 VTCP của \(\Delta \).
\(\left( P \right)\) nhận\(\overrightarrow n \left( {1;1;1} \right)\) là 1 VTPT.
Do \(\Delta \bot \left( P \right) \Rightarrow \overrightarrow {AB} \) và \(\overrightarrow n \) là 2 vectơ cùng phương.
\( \Rightarrow 2t + t' + 3 = - t + 2t' - 1 = - 3t - 2t' + 1 \Leftrightarrow \left\{ \begin{array}{l}3t - t' + 4 = 0\\2t + 4t' - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - 1\\t' = 1\end{array} \right.\)
\( \Rightarrow A\left( {1; - 1; - 4} \right),\,\,B\left( {3;1; - 2} \right) \Rightarrow \overrightarrow {AB} = \left( {2;2;2} \right)//\left( {1;1;1} \right)\).
Vậy phương trình đường thẳng \(\Delta :\,\,\dfrac{{x - 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{1}\).
Có bao nhiêu số nguyên \(m\) để phương trình \(x + 3 = m{e^x}\) có 2 nghiệm phân biệt?
-
A.
$7$
-
B.
$6$
-
C.
$5$
-
D.
Vô số
Đáp án : A
+) Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\).
+) Số nghiệm của phương trình \(m = f\left( x \right)\) là số giao điểm của đồ thị hàm số \(y = m\) và \(y = f\left( x \right)\).
+) Lập BBT hàm số \(y = f\left( x \right)\) và kết luận.
\(x + 3 = m{e^x} \Leftrightarrow m = \dfrac{{x + 3}}{{{e^x}}} = f\left( x \right)\,\,\left( * \right)\,\,\left( {Do\,\,{e^x} > 0\,\,\forall x \in \mathbb{R}} \right)\).
Để phương trình \(x + 3 = m{e^x}\) có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm phân biệt.
Xét hàm số \(f\left( x \right) = \dfrac{{x + 3}}{{{e^x}}}\) ta có: \(f'\left( x \right) = \dfrac{{{e^x} - \left( {x + 3} \right){e^x}}}{{{e^{2x}}}} = \dfrac{{ - x - 2}}{{{e^x}}} = 0 \Leftrightarrow x = - 2\).
BBT:
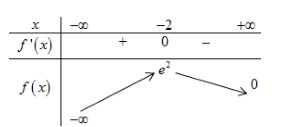
Số nghiệm của phương trình \(m = f\left( x \right)\) là số giao điểm của đồ thị hàm số \(y = m\) và \(y = f\left( x \right)\).
Dựa vào BBT ta có phương trình \(\left( * \right)\) có 2 nghiệm phân biệt \( \Rightarrow 0 < m < {e^2}\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2;3;4;5;6;7} \right\}\).
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {x - 1} \right) + {x^2} - 2x\) đồng biến trên khoảng?

-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( { - 1;0} \right)\)
-
C.
\(\left( {0;1} \right)\)
-
D.
\(\left( { - 2; - 1} \right)\)
Đáp án : A
Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {a;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.
Ta có: \(y' = f'\left( {x - 1} \right) + 2x - 2 = 0\) \( \Leftrightarrow f'\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\).
Đặt \(t = x - 1\) ta có \(f'\left( t \right) + 2t = 0\) \( \Leftrightarrow f'\left( t \right) - \left( { - 2t} \right) = 0\).
Vẽ đồ thị hàm số \(y = f'\left( t \right)\) và \(y = - 2t\) trên cùng mặt phẳng tọa độ ta có:
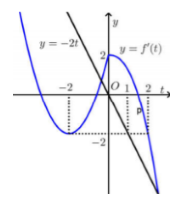
Xét \(y' \ge 0 \Leftrightarrow f'\left( t \right) \ge - 2t \Rightarrow \) Đồ thị hàm số \(y = f'\left( t \right)\) nằm trên đường thẳng \(y = - 2t\).
Xét \(x \in \left( {1;2} \right) \Rightarrow t \in \left( {0;1} \right) \Rightarrow \) thỏa mãn.
Xét \(x \in \left( { - 1;0} \right) \Rightarrow t \in \left( { - 2; - 1} \right) \Rightarrow \) Không thỏa mãn.
Xét \(x \in \left( {0;1} \right) \Rightarrow t \in \left( { - 1;0} \right) \Rightarrow \) Không thỏa mãn.
Xét \(x \in \left( { - 2; - 1} \right) \Rightarrow t \in \left( { - 3; - 2} \right) \Rightarrow \) Không thỏa mãn.
Có bao nhiêu số nguyên \(a \in \left( { - 2019;2019} \right)\) để phương trình \(\dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} = x + a\) có hai nghiệm phân biệt?
-
A.
$0$
-
B.
$2022$
-
C.
$2014$
-
D.
$2015$
Đáp án : D
+) Cô lập \(m\), đưa phương trình về dạng \(a = f\left( x \right)\).
+) Số nghiệm của phương trình \(a = f\left( x \right)\) là số giao điểm của đồ thị hàm số \(y = a\) và \(y = f\left( x \right)\).
+) Lập BBT hàm số \(y = f\left( x \right)\) và kết luận
\(\dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} = x + a \Leftrightarrow f\left( x \right) = \dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} - x = a\,\,\left( * \right)\).
Xét hàm số \(f\left( x \right) = \dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} - x\).
ĐKXĐ: \(\left\{ \begin{array}{l}x + 5 > 0\\\ln \left( {x + 5} \right) \ne 0\\{3^x} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 5\\x + 5 \ne 1\\{3^x} \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 5\\x \ne - 4\\x \ne 0\end{array} \right.\)
\( \Rightarrow D = \left( { - 5; - 4} \right) \cup \left( { - 4;0} \right) \cup \left( {0; + \infty } \right)\).
Ta có:
$f'\left( x \right) = - \frac{1}{{\left( {x + 5} \right){{\ln }^2}\left( {x + 5} \right)}} - \frac{{{3^x}\ln 3}}{{{{\left( {{3^x} - 1} \right)}^2}}} - 1 < 0,\forall x \in D$
BBT:
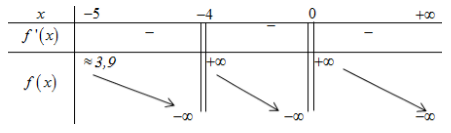
Từ BBT suy ra phương trình (*) có 2 nghiệm \( \Leftrightarrow a \ge 4\).
Kết hợp ĐK \( \Rightarrow a \in \left\{ {4;...;2018} \right\}\). Vậy có 2015 giá trị của \(a\) thỏa mãn.
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( 0 \right) = 3\) và \(f\left( x \right) + f\left( {2 - x} \right) = {x^2} - 2x + 2\,\,\forall x \in \mathbb{R}\). Tích phân \(\int\limits_0^2 {xf'\left( x \right)dx} \) bằng:
-
A.
\( - \dfrac{4}{3}\)
-
B.
\(\dfrac{2}{3}\)
-
C.
\(\dfrac{5}{3}\)
-
D.
\(\dfrac{{ - 10}}{3}\)
Đáp án : D
Sử dụng phương pháp tích phân từng phần.
\(\int\limits_0^2 {xf'\left( x \right)dx} = \int\limits_0^2 {xd\left( {f\left( x \right)} \right)} = \left. {xf\left( x \right)} \right|_0^2 - \int\limits_0^2 {f\left( x \right)dx} = 2f\left( 2 \right) - \int\limits_0^2 {f\left( x \right)dx} \)
Theo bài ra ta có:
\(f\left( x \right) + f\left( {2 - x} \right) = {x^2} - 2x + 2\,\,\forall x \in \mathbb{R} \Rightarrow f\left( 0 \right) + f\left( 2 \right) = 2 \Rightarrow f\left( 2 \right) = 2 - f\left( 0 \right) = - 1\).
\( \Rightarrow \int\limits_0^2 {xf'\left( x \right)dx} = - 2 - \int\limits_0^2 {f\left( x \right)dx} = - 2 - \int\limits_0^2 {f\left( t \right)dt} \).
Đặt \(t = 2 - x \Rightarrow dt = - dx\). Đổi cận \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 2\\x = 2 \Rightarrow t = 0\end{array} \right.\).
\(\begin{array}{l} \Rightarrow \int\limits_0^2 {f\left( t \right)dx} = - \int\limits_2^0 {f\left( {2 - x} \right)dx} = \int\limits_0^2 {f\left( {2 - x} \right)dx} \\ \Rightarrow \int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {f\left( {2 - x} \right)dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {f\left( x \right)dx} + \int\limits_0^2 {f\left( {2 - x} \right)dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {\left[ {f\left( x \right) + f\left( {2 - x} \right)} \right]dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {\left( {{x^2} - 2x + 2} \right)dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \left. {\left( {\dfrac{{{x^3}}}{3} - {x^2} + 2x} \right)} \right|_0^2 = \dfrac{8}{3}\\ \Rightarrow \int\limits_0^2 {f\left( x \right)dx} = \dfrac{4}{3}\end{array}\)
Vậy \(\int\limits_0^2 {xf'\left( x \right)dx} = - 2 - \dfrac{4}{3} = - \dfrac{{10}}{3}\).
Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) (với \(m\) là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?
-
A.
$2$
-
B.
$3$
-
C.
$5$
-
D.
$4$
Đáp án : D
Số điểm cực trị của hàm số \(y = \left| {f\left( x \right)} \right|\) = số cực trị của hàm số \(y = f\left( x \right)\) + số giao điểm của đồ thị hàm số với trục hoành. (Hàm đa thức hoặc hàm số xác định \(\forall x \in \mathbb{R}\))
Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) có TXĐ \(D = \mathbb{R}\).
Xét hàm số \(g\left( x \right) = \dfrac{x}{{{x^2} + 1}} - m\) ta có:
\(g'\left( x \right) = \dfrac{{{x^2} + 1 - x.2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \dfrac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0 \Leftrightarrow x = \pm 1\).
\( \Rightarrow \) Hàm số \(y = g\left( x \right)\) có 2 điểm cực trị.
Xét phương trình hoành độ giao điểm \(\dfrac{x}{{{x^2} + 1}} - m = 0 \Leftrightarrow \dfrac{{x - m\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = 0 \Leftrightarrow - m{x^2} + x - m = 0\), phương trình có \(\Delta = 1 - 4{m^2}\) chưa xác định dấu nên có tối đa 2 nghiệm.
Vậy hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) có tối đa \(2 + 2 = 4\) cực trị.
Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích bằng \(V\). Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,E,\,\,F\) lần lượt là tâm các hình bình hành \(ABCD,\,\,A'B'C'D',\,\,ABB'A',\,\,BCC'B',\,\,CDD'C',\,\,DAA'D'\). Thể tích khối đa diện có các đỉnh \(M,\,\,P,\,\,Q,\,\,E,\,\,F,\,\,N\) bằng:
-
A.
\(\dfrac{V}{4}\)
-
B.
\(\dfrac{V}{2}\)
-
C.
\(\dfrac{V}{6}\)
-
D.
\(\dfrac{V}{3}\)
Đáp án : C
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng .
Sử dụng công thức tính nhanh thể tích khối bát diện đều cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{3}\).
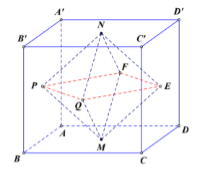
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng 1 \( \Rightarrow {V_{ABCD.A'B'C'D'}} = 1 = V\).
Dễ thấy \(MNPQEF\) là khối bát diện đều cạnh cạnh \(QE = \dfrac{1}{2}BD = \dfrac{{\sqrt 2 }}{2}\).
Vậy \({V_{MNPQEF}} = \dfrac{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^3}\sqrt 2 }}{3} = \dfrac{1}{6} = \dfrac{V}{6}\).
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh \(40\,\left( {cm} \right)\) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \(4{x^2} = {y^4}\) và \(4{\left( {\left| x \right| - 1} \right)^3} = {y^2}\) để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?

-
A.
\(506\,\,\left( {c{m^2}} \right)\)
-
B.
\(747\,\,\left( {c{m^2}} \right)\)
-
C.
\(507\,\,\left( {c{m^2}} \right)\)
-
D.
\(746\,\,\left( {c{m^2}} \right)\)
Đáp án : B
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
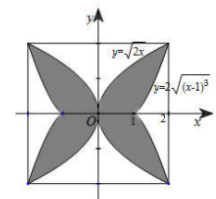
Gắn hệ trục tọa độ như hình vẽ.
Diện tích phần tô đậm là \(S = 4\left[ {\int\limits_0^1 {\left( {\sqrt {2x} - 0} \right)dx} + \int\limits_1^2 {\left( {\sqrt {2x} - 2\sqrt {{{\left( {x - 1} \right)}^3}} } \right)dx} } \right] = \dfrac{{112}}{{15}}\,\,\left( {d{m^2}} \right) \approx 747\,\,\left( {c{m^2}} \right)\).
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| z \right| = 2,\,\,\left| {iw - 2 + 5i} \right| = 1\). Giá trị nhỏ nhất của \(\left| {{z^2} - wz - 4} \right|\) bằng:
-
A.
\(4\)
-
B.
\(2\left( {\sqrt {29} - 3} \right)\)
-
C.
\(8\)
-
D.
\(2\left( {\sqrt {29} - 5} \right)\)
Đáp án : C
Theo bài ra ta có :
+) \(\left| z \right| = 2 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \({I_1}\left( {0;0} \right)\) bán kính \({R_1} = 2\).
\(\left| i \right|\left| {w - \dfrac{{2 - 5i}}{i}} \right| = 1 \Leftrightarrow \left| {w - \left( { - 5 - 2i} \right)} \right| = 1\)
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(w\) là đường tròn tâm \({I_2}\left( { - 5; - 2} \right)\) bán kính \({R_2} = 1\).
Đặt \(T = \left| {{z^2} - wz - 4} \right| = \left| {{z^2} - wz - z.\overline z } \right| = \left| z \right|\left| {z - w - \overline z } \right| = 2\left| {z - w - \overline z } \right|\)
Đặt \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi \Rightarrow z - \overline z = 2bi\).
\( \Rightarrow T = 2\left| {2bi - w} \right|\).
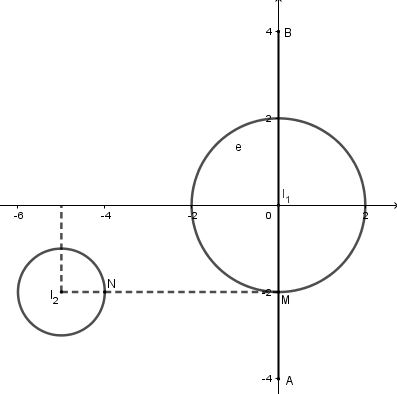
Gọi \(M\left( {0;2b} \right)\) là điểm biểu diễn số phức \(2bi\), \(N\) là điểm biểu diễn số phức \(w\).
\( \Rightarrow T = 2M{N_{\min }} \Leftrightarrow M{N_{\min }}\).
Do \(\left| z \right| = 2 \Rightarrow {a^2} + {b^2} = 4 \Leftrightarrow - 2 \le b \le 2 \Leftrightarrow - 4 \le 2b \le 4\).
\( \Rightarrow \) Tập hợp các điểm \(M\) là đoạn \(AB\) với \(A\left( { 0;-4} \right),\,\,B\left( {0;4} \right)\).
Dựa vào hình vẽ ta thấy \(M{N_{\min }} = 4 \Leftrightarrow N\left( { - 4; - 2} \right),M\left( {0; - 2} \right)\).
Vậy \({T_{\min }} = 2.4 = 8\).
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên

Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
-
A.
\(m < f\left( 0 \right)\)
-
B.
\(m < f\left( 1 \right) - 1\)
-
C.
\(m < f\left( { - 1} \right) + 1\)
-
D.
\(m < f\left( 2 \right)\)
Đáp án : B
- Biến đổi bất phương trình về dạng \(g(x)>m\).
- Xét hàm \(y=g(x)\) và tìm GTNN của \(g(x)\).
- Bài toán thỏa khi \(m<\mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\)
\(\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}\).
Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT đồ thị hàm số \(y = f\left( x \right)\) như sau:
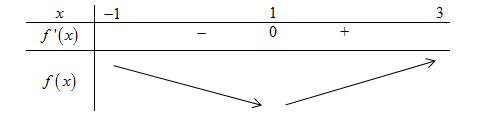
Dựa vào BBT ta thấy \(f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]\).
\(\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow - 1 \le - \sin \dfrac{{\pi x}}{2} \le 1\end{array}\)
\( \Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1\).
Vậy \(m < f\left( 1 \right) - 1\).
Trong không gian Oxyz , cho đường thẳng \(d:\,\,\dfrac{{x - 3}}{2} = \dfrac{{y - 4}}{1} = \dfrac{{z - 2}}{1}\) và 2 điểm \(A\left( {6;3; - 2} \right)\); \(B\left( {1;0; - 1} \right)\). Gọi \(\Delta \) là đường thẳng đi qua \(B\), vuông góc với \(d\) và thỏa mãn khoảng cách từ \(A\) đến \(\Delta \) là nhỏ nhất. Một vectơ chỉ phương của \(\Delta \) có tọa độ :
-
A.
\(\left( {1;1; - 3} \right)\)
-
B.
\(\left( {1; - 1; - 1} \right)\)
-
C.
\(\left( {1;2; - 4} \right)\)
-
D.
\(\left( {2; - 1; - 3} \right)\)
Đáp án : A
+) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(B\) và vuông góc với \(d \Rightarrow \left( P \right):\,\,2x + y + z - 1 = 0\). \(\Delta \) đi qua \(B\) và vuông góc với \(d \Rightarrow \Delta \subset \left( P \right)\).
+) Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(\left( P \right)\) và \(\Delta \) ta có \(AH \le AK\).
+) Do đó để khoảng cách từ \(A\) đến \(\Delta \) là nhỏ nhất \( \Rightarrow H \in \Delta \Rightarrow \Delta \) nhận \(\overrightarrow {BH} \) là 1 VTCP.
Gọi \(\left( P \right)\) là mặt phẳng đi qua \(B\) và vuông góc với \(d \Rightarrow \left( P \right):\,\,2x + y + z - 1 = 0\).
\(\Delta \) đi qua \(B\) và vuông góc với \(d \Rightarrow \Delta \subset \left( P \right)\).
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(\left( P \right)\) và \(\Delta \) ta có \(AH \le AK\).
Do đó để khoảng cách từ \(A\) đến \(\Delta \) là nhỏ nhất \( \Rightarrow H \in \Delta \).
Phương trình \(AH\) đi qua \(A\) và nhận \(\overrightarrow {{u_d}} = \left( {2;1;1} \right)\) là 1 VTCP là \(\left\{ \begin{array}{l}x = 6 + 2t\\y = 3 + t\\z = - 2 + t\end{array} \right.\).
\(\begin{array}{l}H \in AH \Rightarrow H\left( {6 + 2t;3 + t; - 2 + t} \right)\\H \in \left( P \right) \Rightarrow 2\left( {6 + 2t} \right) + 3 + t - 2 + t - 1 = 0 \Leftrightarrow 6t + 12 = 0 \Leftrightarrow t = - 2\\ \Rightarrow H\left( {2;1; - 4} \right)\end{array}\)
\(\Delta \) đi qua \(B,\,\,H\) nhận \(\overrightarrow {BH} \left( {1;1; - 3} \right)\) là 1 VTCP.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |









