Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 9
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 9
Đề bài
Cho góc hình học $uOv$ có số đo $50^\circ $. Xác định số đo của góc lượng giác $\left( {Ou,Ov} \right)$ trong hình dưới đây?

-
A.
$50^\circ $.
-
B.
$330^\circ $.
-
C.
\( - 50^\circ .\)
-
D.
$130^\circ .$
Cho góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo là \(\frac{\pi }{4}\). Số đo của các góc lượng giác nào sau đây có cùng tia đầu là \(Ou\) và tia cuối là \(Ov\)?
-
A.
\(\frac{{3\pi }}{4}\)
-
B.
\(\frac{{5\pi }}{4}\)
-
C.
\(\frac{{7\pi }}{4}\)
-
D.
\(\frac{{9\pi }}{4}\)
Góc có số đo \(\frac{{7\pi }}{4}\) radian bằng bao nhiêu độ?
-
A.
\({315^o}\)
-
B.
\({45^o}\)
-
C.
\({345^o}\)
-
D.
\({275^o}\)
Một đường tròn có bán kính 15 cm. Tìm độ dài cung tròn có góc ở tâm bằng \({30^o}\).
-
A.
\(\frac{{5\pi }}{2}\)
-
B.
\(\frac{{5\pi }}{3}\)
-
C.
\(\frac{{2\pi }}{5}\)
-
D.
\(\frac{\pi }{3}\)
Công thức nào sau đây sai?
-
A.
\(\cos (a - b) = \cos a\cos b + \sin a\sin b\)
-
B.
\(\cos (a + b) = \cos a\cos b + \sin a\sin b\)
-
C.
\(\sin (a - b) = \sin a\cos b - \cos a\sin b\)
-
D.
\(\sin (a + b) = \sin a\cos b + \cos a\sin b\)
Cho dãy số \(({u_n})\) với \({u_n} = 3n + 1,\forall n \in {N^*}\). Giá trị của \({u_3}\) bằng
-
A.
7
-
B.
28
-
C.
10
-
D.
12
Dãy số nào sau đây là dãy số tăng?
-
A.
\( - 1;\,\,0;\,\,3;\,\,8;\,\,16.\)
-
B.
\(1;\,\,4;\,\,16;\,\,9;\,\,25.\)
-
C.
\(0;\,\,3;\,\,8;\,\,24;\,\,15.\)
-
D.
\(0;\,\,3;\,\,12;\,\,9;\,\,6.\)
Xét tính bị chặn của dãy số sau: ${u_n} = 3n - 1$.
-
A.
Bị chặn.
-
B.
Bị chặn trên.
-
C.
Bị chặn dưới.
-
D.
Không bị chặn dưới.
Trong các dãy số sau, dãy số nào là một cấp số cộng?
-
A.
1; -2; -4; -6; -8
-
B.
1; -3; -6; -9; -12
-
C.
1; -3; -7; -11; -15
-
D.
1; -3; -5; -7; -9
Cho dãy số $ - 1;1; - 1;1; - 1;...$ Khẳng định nào sau đây là đúng?
-
A.
Dãy số này không phải là cấp số nhân.
-
B.
Số hạng tổng quát ${u_n} = {1^n} = 1$.
-
C.
Dãy số này là cấp số nhân có ${u_1} = - 1;q = - 1$.
-
D.
Số hạng tổng quát ${u_n} = {\left( { - 1} \right)^{2n}}$.
Mệnh đề nào sai trong các mệnh đề sau?
-
A.
Nếu ba điểm $A,\,\,B,\,\,C$ là ba điểm chung của hai mặt phẳng $(P)$ và $(Q)$ thì $A,\,\,B,\,\,C$ thẳng hàng.
-
B.
Nếu ba điểm $A,\,\,B,\,\,C$ thẳng hàng và hai mặt phẳng $(P)$ và $(Q)$ có điểm chung là $A$ thì $B,\,C$ cũng là hai điểm chung của $(P)$ và $(Q)$.
-
C.
Nếu ba điểm $A,\,\,B,\,\,C$ là ba điểm chung của hai mặt phẳng $(P)$ và $(Q)$ phân biệt thì $A,\,\,B,\,\,C$ không thẳng hàng.
-
D.
Nếu ba điểm $A,\,\,B,\,\,C$ thẳng hàng và $A,\,\,B$ là hai điểm chung của $(P)$ và $(Q)$ thì $\,C$ cũng là điểm chung của $(P)$ và $(Q)$.
Cho tứ diện ABCD. Gọi M là trung điểm của đoạn thẳng BC. Giao tuyến của hai mặt phẳng (AMD) và (BCD) là đường thẳng nào dưới đây?
-
A.
CD
-
B.
BC
-
C.
MA
-
D.
MD
Cho hàm số \(y = \sin x\). Khi đó
a) \(\sin x < 0\) khi \( - \frac{\pi }{2} < x < 0\)
b) Hàm số \(y = \sin x\) lẻ với mọi \(x \in \mathbb{R}\)
c) Phương trình \(\sin x = 1\) có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
d) Hàm số \(y = \sin x\) có chặn dưới là 0
Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn 75% giá trị trong năm liền trước đó.
a) Giá trị của máy photocopy sau 1 năm sử dụng là: \({T_1} = 37,5\) triệu đồng.
b) Giá trị của máy photocopy sau 2 năm sử dụng lớn hơn 30 triệu đồng.
c) Giá trị tiêu hao của chiếc máy photocopy đó sau khoảng thời gian 5 năm kể từ khi mua là \(11,8652\) triệu đồng.
d) Sau 7 năm thì giá trị của máy photocopy con 10% có với giá trị ban đầu.
Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày ($0 \leq t < 24$) cho bởi công thức $h = 3\cos\left( {\dfrac{\pi}{6}t + 1} \right) + 12$. Hỏi thời điểm muộn nhất trong ngày mà độ sâu của mực nước trong kênh thấp nhất là mấy giờ (làm tròn kết quả đến hàng đơn vị)?
Một CLB Toán học tổ chức trò chơi sử dụng đồng xu để xếp thành một cái tháp. Nhóm đã sử dụng 60723 đồng xu để xếp một mô hình tháp. Biết rằng tầng dưới cùng có 3809 đồng xu và cứ lên thêm một tầng thì số đồng xu giảm đi 120 đồng xu. Hỏi mô hình tháp có tất cả bao nhiêu tầng?
Cô Ngọc mua một chiếc ô tô giá 600 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị của ô tô giảm đi 8% (so với năm trước đó). Giả sử sau bốn năm, cô bán xe bằng giá trị còn lại của xe và thêm tiền để mua xe mới giá 800 triệu thì cô phải bù thêm bao nhiêu tiền? (Các phép toán làm tròn đến hàng triệu).
Cho hình chóp S.ABCD có AB // CD, AB = 2CD. Gọi I là trung điểm của cạnh SA. Giao tuyến của hai mặt phẳng (SAB) và (IDC) là đường thẳng IJ. Biết J là điểm nằm trên cạnh SB và IJ = kAB. Tính k.
Lời giải và đáp án
Cho góc hình học $uOv$ có số đo $50^\circ $. Xác định số đo của góc lượng giác $\left( {Ou,Ov} \right)$ trong hình dưới đây?

-
A.
$50^\circ $.
-
B.
$330^\circ $.
-
C.
\( - 50^\circ .\)
-
D.
$130^\circ .$
Đáp án : A
Dựa vào khái niệm góc lượng giác.
Góc ngược chiều kim đồng hồ nên có giá trị dương là 50 độ.
Cho góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo là \(\frac{\pi }{4}\). Số đo của các góc lượng giác nào sau đây có cùng tia đầu là \(Ou\) và tia cuối là \(Ov\)?
-
A.
\(\frac{{3\pi }}{4}\)
-
B.
\(\frac{{5\pi }}{4}\)
-
C.
\(\frac{{7\pi }}{4}\)
-
D.
\(\frac{{9\pi }}{4}\)
Đáp án : D
Góc lượng giác có cùng tia đầu và tia cuối với (Ou, Ov) là \(x = \frac{\pi }{4} + k2\pi \).
Góc lượng giác có cùng tia đầu và tia cuối với (Ou, Ov) là \(x = \frac{\pi }{4} + k2\pi \).
Khi k = 1 thì \(x = \frac{\pi }{4} + 2\pi = \frac{{9\pi }}{4}\).
Góc có số đo \(\frac{{7\pi }}{4}\) radian bằng bao nhiêu độ?
-
A.
\({315^o}\)
-
B.
\({45^o}\)
-
C.
\({345^o}\)
-
D.
\({275^o}\)
Đáp án : A
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\).
Ta có: \(\frac{{7\pi }}{4}rad = \frac{{7\pi }}{4}.\frac{{{{180}^o}}}{\pi } = {315^o}\).
Một đường tròn có bán kính 15 cm. Tìm độ dài cung tròn có góc ở tâm bằng \({30^o}\).
-
A.
\(\frac{{5\pi }}{2}\)
-
B.
\(\frac{{5\pi }}{3}\)
-
C.
\(\frac{{2\pi }}{5}\)
-
D.
\(\frac{\pi }{3}\)
Đáp án : A
Một cung của đường tròn bán kính R và có số đo \(\alpha\) rad thì có độ dài \(l=R\alpha\).
Đổi \({30^o} = \frac{\pi }{6}\) rad.
Ta có \(l = R\alpha = 15.\frac{\pi }{6} = \frac{{5\pi }}{2}\).
Công thức nào sau đây sai?
-
A.
\(\cos (a - b) = \cos a\cos b + \sin a\sin b\)
-
B.
\(\cos (a + b) = \cos a\cos b + \sin a\sin b\)
-
C.
\(\sin (a - b) = \sin a\cos b - \cos a\sin b\)
-
D.
\(\sin (a + b) = \sin a\cos b + \cos a\sin b\)
Đáp án : B
Dựa vào công thức cộng lượng giác.
B sai vì \(\cos (a + b) = \cos a\cos b - \sin a\sin b\).
Cho dãy số \(({u_n})\) với \({u_n} = 3n + 1,\forall n \in {N^*}\). Giá trị của \({u_3}\) bằng
-
A.
7
-
B.
28
-
C.
10
-
D.
12
Đáp án : C
Thay \(n = 3\) vào \({u_n} = 3n + 1,\forall n \in {N^*}\).
Thay \(n = 3\) vào \({u_n} = 3n + 1,\forall n \in {N^*}\) ta được \({u_4} = 3.3 + 1 = 10\).
Dãy số nào sau đây là dãy số tăng?
-
A.
\( - 1;\,\,0;\,\,3;\,\,8;\,\,16.\)
-
B.
\(1;\,\,4;\,\,16;\,\,9;\,\,25.\)
-
C.
\(0;\,\,3;\,\,8;\,\,24;\,\,15.\)
-
D.
\(0;\,\,3;\,\,12;\,\,9;\,\,6.\)
Đáp án : A
\(({u_n})\) là dãy tăng khi và chỉ khi \({u_{n + 1}} > {u_n}\) với mọi \(n \in {\mathbb{N}^*}\).
Chỉ có dãy số A có các số hạng đứng sau luôn lớn hơn số hạng đứng liền trước.
Xét tính bị chặn của dãy số sau: ${u_n} = 3n - 1$.
-
A.
Bị chặn.
-
B.
Bị chặn trên.
-
C.
Bị chặn dưới.
-
D.
Không bị chặn dưới.
Đáp án : C
Dãy số bị chặn nếu nó vừa bị chặn dưới, vừa bị chặn trên.
Tìm giá trị nhỏ nhất, giá trị lớn nhất mà một số hạng của dãy số có thể đạt.
Dãy \(({u_n})\) với \(n \in {\mathbb{N}^*}\) có \(n \ge 1 \Leftrightarrow 3n \ge 3 \Leftrightarrow 3n - 1 \ge 2\).
Vậy dãy bị chặn dưới bởi 2.
Không có giá trị M nào để \({u_n} \le M\) với mọi \(n \in {\mathbb{N}^*}\) nên dãy không bị chặn trên.
Trong các dãy số sau, dãy số nào là một cấp số cộng?
-
A.
1; -2; -4; -6; -8
-
B.
1; -3; -6; -9; -12
-
C.
1; -3; -7; -11; -15
-
D.
1; -3; -5; -7; -9
Đáp án : C
Dãy số \(\left( {{u_n}} \right)\) có tính chất \({u_{n + 1}} = {u_n} + d\) thì được gọi là một cấp số cộng.
Ta thấy dãy số 1; -3; -7; -11; -15 là một cấp số cộng có số hạng đầu và công sai d = -4.
Cho dãy số $ - 1;1; - 1;1; - 1;...$ Khẳng định nào sau đây là đúng?
-
A.
Dãy số này không phải là cấp số nhân.
-
B.
Số hạng tổng quát ${u_n} = {1^n} = 1$.
-
C.
Dãy số này là cấp số nhân có ${u_1} = - 1;q = - 1$.
-
D.
Số hạng tổng quát ${u_n} = {\left( { - 1} \right)^{2n}}$.
Đáp án : C
Dựa vào các định nghĩa cấp số nhân, số hạng tổng quát của cấp số nhân.
Dãy số này là cấp số nhân có ${u_1} = - 1;q = - 1$.
Số hạng tổng quát: \({u_n} = ( - 1).{( - 1)^{n - 1}} = {( - 1)^{n - 1 + 1}} = {( - 1)^n}\).
Mệnh đề nào sai trong các mệnh đề sau?
-
A.
Nếu ba điểm $A,\,\,B,\,\,C$ là ba điểm chung của hai mặt phẳng $(P)$ và $(Q)$ thì $A,\,\,B,\,\,C$ thẳng hàng.
-
B.
Nếu ba điểm $A,\,\,B,\,\,C$ thẳng hàng và hai mặt phẳng $(P)$ và $(Q)$ có điểm chung là $A$ thì $B,\,C$ cũng là hai điểm chung của $(P)$ và $(Q)$.
-
C.
Nếu ba điểm $A,\,\,B,\,\,C$ là ba điểm chung của hai mặt phẳng $(P)$ và $(Q)$ phân biệt thì $A,\,\,B,\,\,C$ không thẳng hàng.
-
D.
Nếu ba điểm $A,\,\,B,\,\,C$ thẳng hàng và $A,\,\,B$ là hai điểm chung của $(P)$ và $(Q)$ thì $\,C$ cũng là điểm chung của $(P)$ và $(Q)$.
Đáp án : C
Dựa vào lý thuyết các tính chất được thừa nhận về đường thẳng và mặt phẳng.
Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến.
Vậy C sai.
Cho tứ diện ABCD. Gọi M là trung điểm của đoạn thẳng BC. Giao tuyến của hai mặt phẳng (AMD) và (BCD) là đường thẳng nào dưới đây?
-
A.
CD
-
B.
BC
-
C.
MA
-
D.
MD
Đáp án : D
Tìm 2 điểm chung của 2 mặt phẳng.
Ta có (AMD) và (BCD) có điểm chung là M, D nên giao tuyến là MD.
Cho hàm số \(y = \sin x\). Khi đó
a) \(\sin x < 0\) khi \( - \frac{\pi }{2} < x < 0\)
b) Hàm số \(y = \sin x\) lẻ với mọi \(x \in \mathbb{R}\)
c) Phương trình \(\sin x = 1\) có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
d) Hàm số \(y = \sin x\) có chặn dưới là 0
a) \(\sin x < 0\) khi \( - \frac{\pi }{2} < x < 0\)
b) Hàm số \(y = \sin x\) lẻ với mọi \(x \in \mathbb{R}\)
c) Phương trình \(\sin x = 1\) có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
d) Hàm số \(y = \sin x\) có chặn dưới là 0
a) Dựa vào góc phần tư của đường tròn lượng giác.
b) Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\).
- Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định.
- Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định.
c) Giải phương trình lượng giác \(\sin x = a\):
- Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm.
- Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành:
\(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\).
d) Xét tập giá trị của hàm số \(y = \sin x\).
a) Đúng. \( - \frac{\pi }{2} < x < 0\) suy ra điểm biểu diễn góc x thuộc góc phần tư thứ IV. Khi đó \(\sin x < 0\).
b) Đúng. Tập xác định: D = R. Mặt khác, \(f( - x) = \sin ( - x) = - \sin x = - f(x)\). Vậy \(y = \sin x\) là hàm số lẻ.
c) Sai. Do \(\sin \frac{\pi }{2} = 1\) nên \(\sin x = \sin \frac{\pi }{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k2\pi }\\{x = \pi - \frac{\pi }{2} + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k2\pi \) với \(k \in \mathbb{Z}\).
d) Sai. Hàm số \(y = \sin x\) có chặn dưới là -1.
Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn 75% giá trị trong năm liền trước đó.
a) Giá trị của máy photocopy sau 1 năm sử dụng là: \({T_1} = 37,5\) triệu đồng.
b) Giá trị của máy photocopy sau 2 năm sử dụng lớn hơn 30 triệu đồng.
c) Giá trị tiêu hao của chiếc máy photocopy đó sau khoảng thời gian 5 năm kể từ khi mua là \(11,8652\) triệu đồng.
d) Sau 7 năm thì giá trị của máy photocopy con 10% có với giá trị ban đầu.
a) Giá trị của máy photocopy sau 1 năm sử dụng là: \({T_1} = 37,5\) triệu đồng.
b) Giá trị của máy photocopy sau 2 năm sử dụng lớn hơn 30 triệu đồng.
c) Giá trị tiêu hao của chiếc máy photocopy đó sau khoảng thời gian 5 năm kể từ khi mua là \(11,8652\) triệu đồng.
d) Sau 7 năm thì giá trị của máy photocopy con 10% có với giá trị ban đầu.
Áp dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\).
a) Đúng. Giá trị của máy photocopy sau 1 năm sử dụng là \({T_1} = 50.75\% = 37,5\) (triệu đồng).
b) Sai. Giá trị của máy photocopy sau 2 năm sử dụng là \({T_2} = {T_1}.75\% = 28,125\) (triệu đồng).
c) Sai. Giá trị của máy photocopy sau n năm sử dụng lập thành một cấp số nhân với số hạng đầu bằng 50 (triệu đồng), công bội 75%.
Giá trị của máy photocopy sau 5 năm sử dụng là \(50.{\left( {75\% } \right)^5}\) (triệu đồng).
Giá trị tiêu hao là \(50 - 50.{\left( {75\% } \right)^5} \approx 38,1348\) (triệu đồng).
d) Sai. Giá trị của máy photocopy sau 7 năm sử dụng là \(50.{\left( {75\% } \right)^7}\) (triệu đồng).
Giá trị của máy photocopy sau 7 năm so với giá ban đầu là \(\frac{{50.{{\left( {75\% } \right)}^7}}}{{50}} \approx 13,35\% \).
Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày ($0 \leq t < 24$) cho bởi công thức $h = 3\cos\left( {\dfrac{\pi}{6}t + 1} \right) + 12$. Hỏi thời điểm muộn nhất trong ngày mà độ sâu của mực nước trong kênh thấp nhất là mấy giờ (làm tròn kết quả đến hàng đơn vị)?
Dựa vào tập giá trị của hàm cos để tìm GTNN.
Mực nước thấp nhất khi h đạt GTNN, khi đó:
\(\cos \left( {\frac{\pi }{6}t + 1} \right) = - 1 \Leftrightarrow \frac{\pi }{6}t + 1 = \pi + k2\pi \)
\( \Leftrightarrow \frac{t}{6} + \frac{1}{\pi } = 1 + 2k \Leftrightarrow t = - \frac{6}{\pi } + 6 + 12k\) \(\left( {k \in \mathbb{Z}} \right)\).
Mà \(0 \le t < 24 \Leftrightarrow 0 \le - \frac{6}{\pi } + 6 + 12k < 24 \Leftrightarrow - 0,34 \le k < 1,66\).
Vì \(k \in \mathbb{Z}\) nên k = 0 hoặc k = 1.
Thời điểm muộn nhất mà mực nước trong kênh thấp nhất là:
\(t = - \frac{6}{\pi } + 6 + 12.1 \approx 16\) (giờ).
Một CLB Toán học tổ chức trò chơi sử dụng đồng xu để xếp thành một cái tháp. Nhóm đã sử dụng 60723 đồng xu để xếp một mô hình tháp. Biết rằng tầng dưới cùng có 3809 đồng xu và cứ lên thêm một tầng thì số đồng xu giảm đi 120 đồng xu. Hỏi mô hình tháp có tất cả bao nhiêu tầng?
Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng.
Vì tầng dưới cùng của mô hình tháp có 3809 đồng xu và cứ lên thêm một tầng thì số đồng xu giảm đi 120 đồng nên ta có một cấp số cộng với số hạng đầu ${u_1} = 3809$ công sai d = -120.
Gọi n là số tầng của tháp nên $n \in {\mathbb{N}^*}$.
Theo đề bài ta có:
\({S_n} = 60723 \Leftrightarrow 3809n + \frac{{n\left( {n - 1} \right)\left( { - 120} \right)}}{2} = 60723\)
\( \Leftrightarrow - 60{n^2} + 3869n - 60723 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}n = 27\\n = \frac{{2249}}{{60}} \approx 37,48\end{array} \right.\)
Vì $n \in \mathbb{Z}$ và với n = 27 thì tầng trên cùng có 689 đồng xu.
Vậy tháp có 27 tầng.
Cô Ngọc mua một chiếc ô tô giá 600 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị của ô tô giảm đi 8% (so với năm trước đó). Giả sử sau bốn năm, cô bán xe bằng giá trị còn lại của xe và thêm tiền để mua xe mới giá 800 triệu thì cô phải bù thêm bao nhiêu tiền? (Các phép toán làm tròn đến hàng triệu).
Áp dụng công thức số hạng tổng quát của cấp số nhân:
\({u_n} = {u_1}{q^{n-1}}\).
Giá trị chiếc xe của cô Ngọc mỗi năm lập thành một cấp số nhân với số hạng đầu \({u_1} = 600\), công bội \(q = 100\% - 8\% = 92\% = 0,92\).
Sau 1 năm, giá trị của chiếc xe là \({u_2}\). Sau 2 năm, giá trị của chiếc xe là \({u_3}\).
Giá trị của chiếc xe sau 4 năm là \({u_5} = {u_1}{q^4} = 600.0,{92^4} \approx 429,835776\) (triệu đồng).
Số tiền cô Ngọc phải bù là \(800 - 429,835776 \approx 370\) (triệu đồng).
Cho hình chóp S.ABCD có AB // CD, AB = 2CD. Gọi I là trung điểm của cạnh SA. Giao tuyến của hai mặt phẳng (SAB) và (IDC) là đường thẳng IJ. Biết J là điểm nằm trên cạnh SB và IJ = kAB. Tính k.
Áp dụng tính chất của hai đường thẳng song song.

Vì AB // CD và I là giao điểm của (SAB) và (IDC) nên giao tuyến của (SAB) và (IDC) là đường thẳng x đi qua I và song song với AB, CD.
Theo đề bài, J thuộc x và J thuộc SB nên J là giao điểm của SB và x.
Theo định lí Thales, vì IJ // AB nên \(\frac{{IS}}{{AI}} = \frac{{SJ}}{{JB}} = 1\) hay J là trung điểm của SB.
Khi đó IJ là đường trung bình của tam giác SAB nên \(IJ = \frac{{AB}}{2} = CD\).
Vậy k = 0,5.
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản.
\(\cos x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \cos x = \cos \frac{\pi }{6} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + k2\pi }\\{x = - \frac{\pi }{6} + k2\pi }\end{array}} \right.\) \((k \in \mathbb{Z})\).
+ Sử dụng kiến thức về hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
+ Sử dụng kiến thức về góc nhân đôi để tính:
\(\tan 2\alpha = \frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }}\);
\(\sin 2\alpha = 2\sin \alpha \cos \alpha \).
+ Sử dụng kiến thức về công thức cộng để tính:
\(\cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \);
\(\tan \left( {\alpha - \beta } \right) = \frac{{\tan \alpha - \tan \beta }}{{1 + \tan \alpha \tan \beta }}\).
Vì \(\frac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha < 0\).
Do đó, \(\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {{\left( {\frac{3}{4}} \right)}^2}} = - \frac{{\sqrt 7 }}{4}\).
a) \(\sin 2\alpha = 2\sin \alpha \cos \alpha \)
\(= 2.\frac{3}{4}.\frac{{ - \sqrt 7 }}{4} = \frac{{ - 3\sqrt 7 }}{8}\).
b) \(\cos \left( {\alpha + \frac{\pi }{3}} \right) = \cos \alpha \cos \frac{\pi }{3} - \sin \alpha \sin \frac{\pi }{3}\)
\(= \frac{{ - \sqrt 7 }}{4}.\frac{1}{2} - \frac{3}{4}.\frac{{\sqrt 3 }}{2} = \frac{{ - \sqrt 7 - 3\sqrt 3 }}{8}\).
c) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{3}{4}}}{{\frac{{ - \sqrt 7 }}{4}}} = \frac{{ - 3\sqrt 7 }}{7}\);
\(\tan 2\alpha = \frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = 3\sqrt 7 \);
\(\tan \left( {2\alpha - \frac{\pi }{4}} \right) = \frac{{\tan 2\alpha - \tan \frac{\pi }{4}}}{{1 + \tan 2\alpha .\tan \frac{\pi }{4}}} = \frac{{3\sqrt 7 - 1}}{{1 + 3\sqrt 7 .1}}\)
\(= \frac{{{{\left( {3\sqrt 7 - 1} \right)}^2}}}{{\left( {3\sqrt 7 - 1} \right)\left( {1 + 3\sqrt 7 } \right)}} = \frac{{32 - 3\sqrt 7 }}{{31}}\).
Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
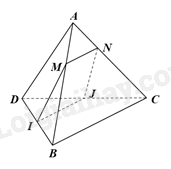
a) Tam giác ABC có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên MN // BC (định lí Thalès đảo).
b) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Do đó, IJ // BC.
Mà MN // BC nên IJ // MN, do đó, MNJI là hình thang.
Hình thang MNJI là hình bình hành khi và chỉ khi MI // NJ // AD.
Mà I là trung điểm của BD. Do đó, MI là đường trung bình của tam giác ADB.
Suy ra M là trung điểm của AB.
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 10
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay (2frac{1}{5}) vòng theo chiều kim đồng hồ?
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
Câu 1: Giá trị biểu thức \(P = {\cos ^2}\frac{\pi }{3} - \tan \frac{\pi }{4} + {\cot ^2}\frac{\pi }{6} + \sin \frac{\pi }{2}\) là:
Câu 1: Cho góc lượng giác (Ov, Ow) có số đo là \(\frac{{4\pi }}{5}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{7\pi }}{5}\). Số đo góc lượng giác (Ou, Ov) là:
Câu 1: Cho góc lượng giác (Ou, Ov) có số đo là (frac{{2pi }}{5}), góc lượng giác (Ou, Ow) có số đo là (frac{{3pi }}{5}). Số đo góc lượng giác (Ov, Ow) là:
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận