50 bài tập Sóng dừng mức độ nhận biết, thông hiểu
Làm đề thiCâu hỏi 1 :
Khoảng cách giữa một nút và một bụng sóng liên tiếp trong hiện tượng sóng dừng là
- A bằng một nửa bước sóng.
- B bằng một bước sóng.
- C bằng 2 lần bước sóng.
- D bằng một phần tư bước sóng.
Đáp án: D
Phương pháp giải:
Phương pháp: Sử dụng lí thuyết về sóng dừng
Lời giải chi tiết:
Đáp án D
Khoảng cách giữa một nút và một bụng sóng liên tiếp trong hiện tượng sóng dừng là một phần tư bước sóng.
Câu hỏi 2 :
Khi có hiện tượng sóng dừng xảy ra trên sợi dây đàn hồi, khoảng cách giữa hai nút sóng liên tiếp bằng
- A một phần tư bước sóng
- B một nửa bước sóng
- C hai lần bước sóng
- D một bước sóng
Đáp án: B
Phương pháp giải:
Phương pháp: Sử dụng lí thuyết về sóng dừng
Lời giải chi tiết:
Đáp án B
Khi có hiện tượng sóng dừng, khoảng cách giữa nút sóng liên tiếp là một nửa bước sóng
Câu hỏi 3 :
Trên một sợi dây đang có sóng dừng, sóng truyền trên dây có bước sóng là λ. Khoảng cách giữa hai nút sóng liên tiếp bằng
- A
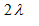
- B
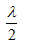
- C
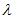
- D
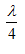
Đáp án: B
Phương pháp giải:
Phương pháp: Khoảng cách giữa hai nút liên tiếp là $${\lambda \over 2}$$
Lời giải chi tiết:
Đáp án B
Trên sợi dây có sóng dừng khoảng cách giứa hai nút liên tiếp là một nửa bước sóng
Câu hỏi 4 :
Nhận xét nào sau đây là sai khi nói về các hiện tượng sóng dừng:
- A Khoảng cách giữa hai nút sóng hay hai bụng sóng liên tiếp bằng nửa bước sóng
- B Sóng dừng trên dây đàn là sóng ngang, trong cột khí của ống sáo, kèn là sóng dọc
- C Mọi điểm nằm giữa hai nút sóng liền kề luôn dao động cùng pha.
- D Bụng sóng và nút sóng dịch chuyển với tốc độ bằng tốc độ lan truyền sóng
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết đại cương về sóng cơ học.
Lời giải chi tiết:
Đáp án D
Bụng sóng và nút sóng luôn cố định
Câu hỏi 5 :
Trên một sợi dây đang có sóng dừng. Hai điểm trên sợi dây cách nhau π/3 thì độ lệch pha có thể là
- A 0,5π.
- B π.
- C 2π/3
- D π/3.
Đáp án: B
Phương pháp giải:
Phương pháp: Áp dụng lý thuyết về sóng dừng
Lời giải chi tiết:
Đáp án B
+ Với hiện tượng sóng dừng thì các phần tử chỉ có thể dao động cùng pha hoặc ngược pha.
Câu hỏi 6 :
Khi sóng cơ truyền trên sợi dây bị phản xạ tại đầu cố định thì
- A tần số của sóng phản xạ luôn nhỏ hơn tần số của sóng tới
- B sóng phản xạ luôn cùng pha với sóng tới ở điểm phản xạ
- C sóng phản xạ luôn ngược pha với với sóng tới ở điểm phản xạ
- D tần số của sóng phản xạ luôn lớn hơn tần số của sóng tới
Đáp án: C
Phương pháp giải:
Phương pháp: Sử dụng lí thuyết về sóng phản xạ
Lời giải chi tiết:
Đáp án C
Cách giải:
Khi sóng cơ truyền trên sợi dây bị phản xạ tại đầu cố định thì sóng phản xạ luôn luôn ngược pha với sóng tới ở điểm phản xạ
=> Chọn C
Câu hỏi 7 :
Một sợi dây đàn hồi AB có chiều dài 15cm và hai đầu cố định. Khi chưa có sóng thì M và N là hai điểm trên dây với với AM = 4cm và BN = 8 cm. Khi xuất hiện sóng dừng, quan sát thấy trên dây có 5 bụng sóng và biên độ của bụng là 1cm. Tỉ số giữa khoảng cách lớn nhất và khoảng cách nhỏ nhất giữa hai điểm M, N xấp xỉ bằng
- A 1,5
- B 1,4
- C 1,3
- D 1,2
Đáp án: D
Phương pháp giải:
Phương pháp: Sử dung công thức sóng dừng trên dây 2 đầu cố định $l = k\frac{\lambda }{2}$
+ Biên độ sóng dừng: $a = A\sin \left( {\frac{{2\pi d}}{\lambda }} \right)cm$
Lời giải chi tiết:
Đáp án D
Cách giải:
Ta có: $l = k\frac{\lambda }{2} \leftrightarrow 15 = 5\frac{\lambda }{2} \to \lambda = 6cm$
Biên độ sóng: $a = 1\sin \left( {\frac{{2\pi d}}{\lambda }} \right)cm$
Ta có: Biên độ sóng tại M và tại N đều bằng $\frac{{\sqrt 3 }}{2}cm$ nhưng ngược pha nhau
Theo định lý pytago: $M{N_{{\text{max}}}} = \sqrt {{{\left( {2.0.5\sqrt 3 } \right)}^2} + {3^2}} = 2\sqrt 3 cm$
d = AN - AM = (15 - 8) - 4 = 3cm = MNmin
=> tỉ số $\frac{{M{N_{{\text{max}}}}}}{{M{N_{\min }}}} = \frac{{2\sqrt 3 }}{3} = 1,155$ => Chọn D
Câu hỏi 8 :
Trên một sợi dây đàn hồi đang có sóng dừng . Khoảng cách từ một nút đến một bụng kề nó bằng
- A một phần tư bước sóng
- B một bước sóng
- C hai bước sóng
- D nửa bước sóng
Đáp án: A
Lời giải chi tiết:
Đáp án A
Câu hỏi 9 :
Dây đàn hồi AB dài 24cm với đầu A cố định, đầu B nối với nguồn sóng. M và N là hai điểm trên dây thành 3 đoạn bằng nhau khi dây duỗi thẳng. Khi trên dây xuất hiện sóng dừng, quan sát thấy có hai bụng và biên độ của bụng sóng là \(2\sqrt 3 cm\), B gần sát một nút sóng. Tỉ số khoảng cách lớn nhất và nhỏ nhất giữa vị trí của M và của N khi dây dao động là:
- A 1,5
- B 1,4
- C 1,25
- D 1,2
Đáp án: C
Phương pháp giải:
Phương pháp:Điều kiện có sóng dừng trên dây hai đầu cố định
Công thức tính biên độ của sóng dừng
Lời giải chi tiết:
Đáp án C
Cách giải:
AM = MN = NB = 8cm
Trên dây có sóng dừng với 2 bụng sóng \( \Rightarrow l = 2.\frac{\lambda }{2} = 24 \Rightarrow \lambda = 24cm\)
Công thức tính biên độ của sóng \(A = 2\sqrt 3 \sin \frac{{2\pi .d}}{\lambda }\) (d là khoảng cách tính từ điểm khảo sát đến nút gần nhất)
Thay dM và dN vào công thức ta thấy biên độ sóng tại M và N đều bằng 3cm nhưng ngược pha nhau
=> Khoảng cách lớn nhất giữa M và N là: \(M{N_{\max }} = \sqrt {{{\left( {2.3} \right)}^2} + {8^2}} = 10cm\)
Khoảng cách nhỏ nhất giữa M và N là: MNmin = 8cm
=> Tỉ số khoảng cách lớn nhất và nhỏ nhất là: 10/8 = 1,25
Câu hỏi 10 :
Một sợi dây đàn hồi căng ngang đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là điểm bụng gần A nhất, I là trung điểm của AB với AB = 10 cm. Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại I là 0,2s. Quãng đường sóng truyền đi trong thời gian 2s là
- A 1 m
- B 0,5 m
- C 2 m
- D 1,5 m
Đáp án: A
Phương pháp giải:
Phương pháp: Khoảng cách giữa 1 nút và bụng gần nhất là $\frac{\lambda }{4}$
+ Quãng đường sóng truyền đi: S = v.t
Lời giải chi tiết:
Đáp án A
Cách giải:
Vì B là điểm bụng gần nút A nhất $AB = \frac{\lambda }{4} = 10 \to \lambda = 40cm$
Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại I là: $\frac{T}{4} = 0,2{\text{s}} \to T = 0,8{\text{s}}$
Vận tốc truyền sóng: $v = \frac{\lambda }{T} = \frac{{0,4}}{{0,8}} = 0,5m/s$
Quãng đường sóng truyền đi trong thời gian 2s là: S = v.t = 0,5 .2 = 1m
=> Chọn A
Câu hỏi 11 :
Một sợi dây có chiều dài 1m hai đầu cố định. Kích thích cho sợi dây dao động với tần số f thì trên dây xuất hiện sóng dừng. Biết tần số chỉ có thể thay đổi trong khoảng từ 300Hz đến 450Hz. Tốc độ truyền dao động là 320m/s. Tần số sóng bằng
- A 320Hz
- B 400 Hz
- C 420 Hz
- D 300 Hz
Đáp án: A
Phương pháp giải:
Phương pháp: Điều kiện có sóng dừng trên dây hai đầu cố định
Lời giải chi tiết:
Đáp án A
Cách giải:
Ta có:\(l = k{\lambda \over 2} = k{v \over {2f}} \Rightarrow f = {{kv} \over {2l}} = {{k.320} \over {2.1}} = 160k\)
Mà:\(300 \leqslant 160k \leqslant 450 \Rightarrow 1,875 \leqslant k \leqslant 2,8125 \Rightarrow k = 2 \Rightarrow f = 320Hz\)
Câu hỏi 12 :
Một nam châm điện có dòng điện xoay chiều tần số 50Hz đi quA. Đặt nam châm điện phía trên một dây thép AB căng ngang với hai đầu cố định, chiều dài sợi dây 60cm. Ta thấy trên dây có sóng dừng với 2 bó sóng. Tính vận tốc sóng truyền trên dây?
- A 60 m/s
- B 60 cm/s
- C 6 m/s
- D 30 m/s
Đáp án: A
Phương pháp giải:
Phương pháp: Điều kiện có sóng dừng trên dây
Lời giải chi tiết:
Đáp án A
Cách giải:
Tần số của nam châm điện f = 50Hz
Ta có chu kì sóng trên dây: f’ = 2f = 100Hz
l = 60 cm, k = 2 (số bó sóng)
Mặt khác: $l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to v = \frac{{l.2f}}{k} = \frac{{0,6.2.100}}{2} = 60m/s$
=> Chọn A
Câu hỏi 13 :
Sóng dừng trên sợi dây hai đầu cố định có chiều dài l = 10 cm; bước sóng λ = 2 cm số bụng sóng là
- A 6
- B 5
- C 11
- D 10
Đáp án: D
Phương pháp giải:
Phương pháp: Áp dụng điều kiện có sóng dừng trên sợi dây có hai đầu cố định \(l = k\frac{\lambda }{2}\)
Lời giải chi tiết:
Đáp án D
Cách giải:
Số bụng sóng xuất hiện trên sợi dây là \(l = k\frac{\lambda }{2} = > 10 = 10.\frac{2}{2} = 10\)
Câu hỏi 14 :
Trên một sợi dây dài 2,1m đang có sóng dừng với tần số 100 Hz người ta thấy ngoài hai đầu cố định còn có 6 điểm khác luôn đứng yên. Vận tốc truyền sóng trên dây là
- A 84 m/s
- B 30 m/s
- C 60 cm/s
- D 60 m/s
Đáp án: A
Phương pháp giải:
Phương pháp : Áp dụng điều kiện có sóng dừng trên sợi dây có hai đầu cố định \(l = k\frac{\lambda }{2}\)
Lời giải chi tiết:
Đáp án A
Cách giải :
Khi sóng dừng xuất hiện trên sợi dây có hai đầu cố định với 6 nút sóng tương ứng với 5 bó sóng khi đó ta có: \(l = k\frac{\lambda }{2} = > 2,1 = 5\frac{\lambda }{2} = > \lambda = 0,84m\)
Vận tốc truyền sóng trên dây là \(v = \lambda f = 0,84.100 = 84m/s\)
Câu hỏi 15 :
Xét hiện tượng sóng dừng trên dây đàn hồi nhẹ AB. Đầu A dao động theo phương vuông góc với sợi dây có biên độ A. Khi đầu B cố định thì sóng phản xạ tại B sẽ
- A ngược pha với sóng tới tại tại B
- B lệch pha π/3 với sóng tới tại B
- C vuông pha với sóng tới tại B
- D cùng pha với sóng tới tại B
Đáp án: A
Lời giải chi tiết:
Đáp án A
Khi đầu B cố định thì sóng phản xạ tại A sẽ ngược pha với sóng tới tại B
Câu hỏi 16 :
Dây AB căng nằm ngang dài 2m, hai đầu A và B cố định, tạo một sóng dừng trên dây với tần số 50Hz, trên đoạn AB thấy có 5 nút sóng. Tốc độ truyền sóng trên dây là:
- A 100m/s
- B 50m/s
- C 25cm/s
- D 2,5cm/s
Đáp án: B
Phương pháp giải:
Phương pháp: Sử dụng công thức sóng dừng trên dây 2 đầu cố định: $l = k\frac{\lambda }{2} = k\frac{v}{{2f}}$
Lời giải chi tiết:
Đáp án B
Cách giải:
Ta có, trên AB có 5 nút sóng => số bụng sóng k = 4
Chiều dài dây: $l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to v = \frac{{l.2f}}{k} = \frac{{2.2.50}}{4} = 50m/s$
=> Chọn B
Câu hỏi 17 :
Trên một sợi dây căng ngang với hai đầu cố định đang có sóng dừng. Quan sát những điểm có cùng biên độ a (0 < a < amax) thì thấy chúng cách đều nhau và khoảng cách giữa hai điểm liên tiếp bằng 15cm. Bước sóng của sóng trên dây có giá trị bằng:
- A 60cm
- B 90cm
- C 30cm
- D 45cm
Đáp án: A
Phương pháp giải:
Phương pháp: Không tính bụng và nút thì các điểm liên tiếp cách đều và có biên độ bằng nhau cách nhau khoảng d = λ/4
Lời giải chi tiết:
Đáp án A
Cách giải:
Theo bài ra ta có: \(\frac{\lambda }{4} = 15cm \Rightarrow \lambda = 60cm\)
Câu hỏi 18 :
Sóng dừng được tạo thành trên một sợi dây đàn hồi có phương trình \(u = 2\sin \frac{{\pi x}}{4}c{\text{os}}\left( {20\pi t + \frac{\pi }{2}} \right)\), trong đóu là li độ dao động của một phần tử trên dây là vị trí cân bằng của nó cách gốc toạ độ O một đoạn bằng x (x tính bằng cm, t tính bằng s). Tốc độ truyền sóng trên sợi dây này bằng
- A 80cm/s
- B 40cm/s
- C 20cm/s
- D 60cm/s
Đáp án: A
Phương pháp giải:
Phương pháp: Đồng nhất với phương trình sóng dừng và áp dụng công thức tốc độ truyền sóng v = λ/T
Lời giải chi tiết:
Đáp án A
Cách giải:
Ta có:
\(\left\{ \matrix{
{{2\pi x} \over \lambda } = {{\pi x} \over 4} \hfill \cr
\omega = 20\pi \hfill \cr} \right. \Rightarrow \left\{ \matrix{
\lambda = 8cm \hfill \cr
T = {1 \over {10}}s \hfill \cr} \right. \Rightarrow v = {\lambda \over T} = 80cm/s\)
Câu hỏi 19 :
Một sợi dây dài 1,2m, hai đầu cố định. Khi tạo sóng dừng trên dây, ta đếm được có tất cả 5 nút trên dây (kể cả 2 đầu). Bước sóng của dao động là:
- A 30cm
- B 24cm
- C 60cm
- D 48cm
Đáp án: C
Lời giải chi tiết:
Chọn đáp án C
+ Điều kiện để có sóng dừng trên dây với hai đầu cố định \(l = n\frac{\lambda }{2}\) với n là số bó sóng, trên dây có 5 nút \( \to n = 4\).
\( \to \lambda = \frac{{2.1,2}}{4} = 60\,\,cm.\)
Câu hỏi 20 :
Trong sóng dừng trên dây, hiệu số pha của hai điểm trên dây nằm đối xứng qua một nút là
- A π rad .
- B 0 rad.
- C 0,5π rad.
- D 0,25π rad.
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Khi xảy ra sóng dừng, hai điểm đối xứng nhau qua một nút thì dao động ngược pha nhau \( \to \Delta \varphi = \pi \).
Câu hỏi 21 :
Nút, bụng của sóng dừng là gì ?
Lời giải chi tiết:
Nút là những điểm tại đó biên độ giao động bằng không.
Bụng là những điểm tại đó biên độ giao động cực đại
Câu hỏi 22 :
Trên một sợi dây đàn hồi đang có sóng dừng. Biết tần số 20 Hz và tốc độ truyền sóng là 80cm/s Khoảng cách từ một nút đến một bụng kề nó bằng
- A 6 cm
- B 2cm
- C 4 cm
- D 1 cm
Đáp án: D
Phương pháp giải:
Khoảng cách từ một nút đến một bụng kề nó bằng λ/4
Lời giải chi tiết:
Đáp án D
Bước sóng: λ = v/f = 80/20 = 4cm
=> Khoảng cách từ một nút đến một bụng kề nó bằng: λ/4 = 4/4 = 1cm
Câu hỏi 23 :
Một sợi dây dài 2 m với hai đầu cố định, đang có sóng dừng. Sóng truyền trên dây với tốc độ 20 m/s. Biết rằng tần số của sóng truyền trên dây có giá trị trong khoảng từ 11Hz đến 19Hz. Tính cả hai đầu dây, số nút sóng trên dây là
- A 5
- B 3
- C 4
- D 2
Đáp án: C
Phương pháp giải:
Áp dụng điều kiện có sóng dừng trên sợi dây có hai đầu cố định \(l = k\frac{\lambda }{2}\)
Lời giải chi tiết:
Đáp án C
Theo bài ra ta có \(\begin{array}{l}l = k\frac{\lambda }{2} = k\frac{v}{{2f}} = > f = \frac{{kv}}{{2l}} = 5k(k \in N)\\11 \le 5k \le 19 = > k = 3\end{array}\). Vậy kể cả hai đầu dây số nút sóng trên dây là 4
Câu hỏi 24 :
Một sợi dây AB đàn hồi, căng ngang dài ℓ = 240cm, hai đầu cố định đang có sóng dừng ổn định. Bề rộng của bụng sóng là 4a. Khoảng cách gần nhất giữa hai điểm dao động cùng pha có cùng biên độ bằng \(a\sqrt 3 \)
là 10 cm. Số bụng sóng trên AB là
- A 4
- B 8
- C 6
- D 10
Đáp án: B
Lời giải chi tiết:
Bụng sóng rộng 4a = > biên độ bụng sóng là 2a.
\(\begin{array}{l}
2a.\left| {\sin \left( {\frac{{2\pi (d - x)}}{\lambda }} \right)} \right| = a\sqrt 3 \\
\sin \left( {\frac{{2\pi (d - x)}}{\lambda }} \right) = \sin \frac{\pi }{3}\\
d = \frac{\lambda }{4};x = 5cm\\
= > \lambda = 60cm
\end{array}\)
Số bụng sóng là:
\(l = n.\frac{\lambda }{2} = > n = 240:30 = 8\)
Câu hỏi 25 :
Đo tốc độ truyền sóng trên một sợi dây đàn hồi bằng cách bố trí thí nghiệm sao cho có sóng dừng trên dây. Tần số sóng hiển thị trên máy phát tần số f = 120 Hz, khoảng cách giữa 3 nút sóng liên tiếp là 20 cm. Kết quả đo tốc độ truyền sóng trên dây là:
- A 16 m/s.
- B 120 m/s.
- C 12 m/s.
- D 24 m/s.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Câu hỏi 26 :
Trên một sợi dây đàn hồi dài 1m, hai đầu cố định, có sóng dừng với 2 bụng sóng. Bước sóng của sóng truyền trên đây là
- A 1m.
- B 0,5m.
- C 2m
- D 0,25m
Đáp án: A
Phương pháp giải:
Điều kiện có sóng dừng trên dây có hai đầu cố định: \(\ell =k\frac{\lambda }{2}\)
Lời giải chi tiết:
Có hai bụng sóng tương đương với có 2 bó sóng.
Ta có \(\ell =k\frac{\lambda }{2}=2.\frac{\lambda }{2}\)= 1m nên bước sóng λ = 1m
Câu hỏi 27 :
Xét hiện tượng sóng dừng trên một sợi dây AB đàn hồi. Nếu đầu A nối với nguồn dao động, đầu B cố định thì sóng tới và sóng phản xạ tại B sẽ
- A ngược pha
- B vuông pha
- C lệch pha π/4
- D cùng pha
Đáp án: A
Phương pháp giải:
Nếu vật cản cố định thì sóng phản xạ ngược pha so với sóng tới
Lời giải chi tiết:
Đầy B cố định thì sóng phản xạ ngược pha sóng tới.
Chọn A
Câu hỏi 28 :
Chọn câu trả lời đúng. Ứng dụng của hiện tượng sóng dừng là để
- A xác định tần số sóng
- B xác định chu kỳ sóng
- C xác định năng lượng sóng
- D Xác định tốc độ truyền sóng
Đáp án: D
Phương pháp giải:
Ứng dụng của hiện tượng sóng dừng là để xác định tốc độ truyền sóng
Lời giải chi tiết:
Ứng dụng của hiện tượng sóng dừng là để xác định tốc độ truyền sóng
Chọn D
Câu hỏi 29 :
Trên một sợi dây dài 1,5m , có sóng dừng được tạo ra, ngoài 2 đầu dây người ta thấy trên dây còn có 4 điểm không dao động . Biết tốc độ truyền sóng trên sợi dây là 45m/s. Tần số sóng bằng
- A 60Hz
- B 75Hz.
- C 45Hz
- D 90Hz.
Đáp án: B
Phương pháp giải:
Sóng dừng trên dây hai đầu cố định thì thõa mãn đk chiều dài dây :
\(l = k.\frac{\lambda }{2}\)
với k là số bụng sóng.
Áp dụng công thức:
\(\lambda = \frac{v}{f}\)
Lời giải chi tiết:
Trên dây ngoài 2 đầu dây người ta thấy trên dây còn có 4 điểm không dao động vậy có 5 bụng.
Ta có:
\(l = k.\frac{\lambda }{2} \Leftrightarrow 1,5 = 5.\frac{\lambda }{2} \Rightarrow \lambda = 0,6m\)
Áp dụng công thức:
\(\lambda = \frac{v}{f} \Rightarrow f = \frac{v}{\lambda } = \frac{{45}}{{0,6}} = 75Hz\)
Chọn B
Câu hỏi 30 :
Sóng truyền trên một sợi dây. Ở đầu dây cố định pha của sóng tới và của sóng phản xạ chênh nhau một lượng bằng bao nhiêu?
- A $\frac{3\pi }{2}+2k\pi $
- B $2k\pi $.
- C $\frac{\pi }{2}+2k\pi $.
- D $\left( 2k+1 \right)\pi $.
Đáp án: D
Phương pháp giải:
Tính chất của sóng dừng, sóng tới và sóng phản xạ luôn ngược pha nhau
Lời giải chi tiết:
Sóng truyền trên sợi dây, tại đầu cố định sóng tới và sóng phản xạ luôn ngược pha nhau .
Đáp án D
Câu hỏi 31 :
Trên một sợi dây dài 0,9 m có sóng dừng. Kể cả hai nút ở hai đầu dây thì trên dây có 10 nút sóng. Biết tần số của sóng truyền trên dây là 200Hz. Sóng truyền trên dây có tốc độ là:
- A 40 cm/s.
- B 90 cm/s.
- C 40 m/s.
- D 90 m/s.
Đáp án: C
Phương pháp giải:
Lí thuyết về sóng dừng trên dây hai đầu cố định.
Lời giải chi tiết:
Cách giải:
Số bó sóng trên dây là 9 → \(9\frac{\lambda }{2} = 0,9m \Rightarrow \lambda = 0,2m\)
Tốc độ truyền sóng trên dây v = λf = 0,2.200 = 40 m/s
→ Chọn C
Câu hỏi 32 :
Dùng dòng điện xoay chiều có tần số f cung cấp cho loa điện động trong bộ thí nghiệm sóng dừng trên dây để tạo nguồn dao động. Khi đó nguồn dao động với
- A Chu kì bằng 2T.
- B tần số bằng 2f.
- C Tần số bằng f.
- D Chu kì bằng T.
Đáp án: B
Phương pháp giải:
Dao động cưỡng bức
Lời giải chi tiết:
dòng điện tần số f gây ra dao động tần số 2f trên loa điện động, tức là ta đã đặt một ngoại lực cưỡng bức tần số 2f vào dây, nên dây sẽ dao động với tần số 2f
Câu hỏi 33 :
Trên một sợi dây đàn hồi dài 1,8 m, hai đầu cố định, đang có sóng dừng với 6 bụng sóng. Biết sóng truyền trên dây có tần số 100 Hz. Tốc độ truyền sóng trên dây là
- A 10 m/s
- B 20 m/s
- C 60 m/s
- D 600 m/s
Đáp án: C
Phương pháp giải:
Áp dụng công thức sóng dừng hai đầu cố định:
\(\text{l = k}\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{2}}\), trong đó: k là số bụng sóng
Lời giải chi tiết:
Ta có: \(\text{l = k}\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{2}}\Rightarrow \text{ }\!\!\lambda\!\!\text{ = }\frac{\text{2}\text{.l}}{\text{k}}\text{ = }\frac{\text{2}\text{.1,8}}{\text{6}}\text{ = 0,6 (m)}\)
Tốc độ truyền sóng trên dây:
\(\text{v = }\!\!\lambda\!\!\text{ }\text{.f}=0,6.100=\text{60 (m/s)}\)
Chọn C
Câu hỏi 34 :
Trên một dợi dây đàn hồi dài 1,2 m, hai đầu cố định, đang có sóng dừng, biết bước sóng λ = 0,4 m. Số bụng sóng trên dây là
- A 3
- B 7
- C 4
- D 6
Đáp án: D
Phương pháp giải:
Điều kiện có sóng dừng trên dây hai đầu cố định:
\(l = k.\frac{\lambda }{2}\)
với k là số bụng sóng
Lời giải chi tiết:
Áp dụng công thức \(l = k.\frac{\lambda }{2}\) . Suy ra k = 6.
Vậy trên dây có 6 bụng.
Chọn D
Câu hỏi 35 :
Sóng truyền trên một sợi dây có hai đầu cố định với bước sóng 60cm. Trên dây có sóng dừng với khoảng cách giữa hai điểm nút liên tiếp là:
- A 120cm
- B 15cm
- C 30cm
- D 60cm
Đáp án: C
Phương pháp giải:
Phương pháp:
Khoảng cách giữa hai nút liên tiếp là \(\frac{\lambda }{2}\)
Lời giải chi tiết:
Cách giải:
Khoảng cách giữa hai nút liên tiếp là \(\frac{\lambda }{2} = \frac{{60}}{2} = 30cm\)
Chọn C
Câu hỏi 36 :
Trên một sợi dây đàn hồi đang có sóng dừng. Biết khoảng cách ngắn nhất giữa một nút sóng và vị trí cân bằng của một bụng sóng là 0,25 m. Sóng truyền trên dây với bước sóng là:
- A 1,5 m
- B 2,0 m.
- C 0,5 m
- D
1,0 m
Đáp án: D
Phương pháp giải:
Biết khoảng cách ngắn nhất giữa một nút sóng và vị trí cân bằng của một bụng sóng là: \(\frac{\lambda }{4}\).
Lời giải chi tiết:
Biết khoảng cách ngắn nhất giữa một nút sóng và vị trí cân bằng của một bụng sóng là: \(\frac{\lambda }{4}\).
Sóng truyền trên dây với bước sóng là: \(\lambda =4.0,25=1(m)\)
Chọn D
Câu hỏi 37 :
Trên một sợi dây đàn hồi dài 0,8 m hai đầu cố định đang có sóng dừng với 5 nút sóng (kể cả hai đầu dây). Biết khoảng thời gian giữa hai lần liên tiếp mà mọi điểm trên dây đều có cùng li độ bằng 0,1 s. Tốc độ truyền sóng trên dây bằng
- A
4,0 m/s.
- B
1,6 m/s.
- C
1,0 m/s.
- D
2,0 m/s.
Đáp án: D
Phương pháp giải:
Áp dụng công thức điều kiện có sóng dừng với hai đầu cố định \(l = k\frac{\lambda }{2}\), số nút là (k + 1) và công thức của tốc độ truyền sóng
Lời giải chi tiết:
\(l = k\frac{\lambda }{2} \Rightarrow \lambda = \frac{{2l}}{k} = \frac{{2.0,8}}{4} = 0,4(m)\)
Khoảng thời gian giữa hai lần liên tiếp mà mọi điểm trên dây đều có cùng li độ là \(\frac{T}{2} = 0,1 \Rightarrow T = 0,2(s)\)
Tốc độ truyền sóng trên dây: \(v = \frac{\lambda }{T} = \frac{{0,4}}{{0,2}} = 2(m/s)\)
Chọn D
Câu hỏi 38 :
Một sợi dây đàn hồi dài 30cm có hai đầu cố định. Trên dây đang có sóng dừng với 3 bụng sóng. Sóng trên dây có bước sóng là
- A
20cm
- B
40cm
- C
10cm
- D
60cm
Đáp án: A
Phương pháp giải:
Điều kiện tồn tại sóng dừng trên dây với hai đầu cố định là: \(L=k\frac{\lambda }{2}\)
Với k là số bó sóng hoặc số bụng sóng trên dây. Số nút sóng trên dây lúc này là k + 1.
Lời giải chi tiết:
Ta có: \(L=k\frac{\lambda }{2}\Leftrightarrow 30=3\frac{\lambda }{2}\Leftrightarrow \lambda =20\left( cm \right)\)
Chọn A
Câu hỏi 39 :
Một sợi dây dài 48cm có hai đầu cố định. Trên dây đang có sóng dừng với 2 bụng sóng. Sóng truyền trên dây có bước sóng là
- A 48cm
- B
24cm
- C
96cm
- D
32cm
Đáp án: A
Phương pháp giải:
Điều kiện tồn tại sóng dừng trên dây với hai đầu cố định là: \(L=k\frac{\lambda }{2}\)
Với k là số bó sóng hoặc số bụng sóng trên dây. Số nút sóng trên dây lúc này là k + 1.
Lời giải chi tiết:
Ta có: \(L=k\frac{\lambda }{2}\Leftrightarrow 48=2\frac{\lambda }{2}\Leftrightarrow \lambda =48\left( cm \right)\)
Chọn A
Câu hỏi 40 :
Một dây đàn dài 40 cm, căng ở hai đầu cố định, khi dây dao động với tần số 600Hz ta quan sát trên dây có sóng dừng với hai bụng sóng. Tốc độ sóng trên dây là
- A V = 120 m/s
- B v = 480 m/s
- C v = 240 m/s
- D v = 79,8 m/s
Đáp án: C
Phương pháp giải:
Sóng dừng trên dây hai đầu cố định thì :
\(l = k.\frac{\lambda }{2} = k.\frac{v}{{2f}}\)
Với k là số bụng sóng (bó sóng).
Lời giải chi tiết:
Từ điều kiện có sóng dừng trên dây hai đầu cố định ta có :
\(l = k.\frac{\lambda }{2} = k.\frac{v}{{2f}} \Rightarrow v = \frac{{2lf}}{k} = \frac{{2.0,4.600}}{2} = {240_{}}(m/s)\)
Chọn C.
Câu hỏi 41 :
Quan sát sóng dừng trên một sợi dây đàn hồi, người ta thấy khoảng thời gian giữa 2 thời điểm gần nhất mà dây duỗi thẳng là 0,1s, khoảng cách giữa 2 điểm luôn đứng yên kề nhau là 5 cm. Tốc độ truyền sóng trên dây là
- A 25 cm/s
- B 50 cm/s
- C 20 cm/s
- D 100 cm/s
Đáp án: B
Phương pháp giải:
Khoảng thời gian liên tiếp hai lần dây duỗi thẳng là nửa chu kì.
Khoảng cách giữa hai nút liên tiếp là \(\frac{\lambda }{2}\)
Áp dụng công thức tính bước sóng \(\lambda = v.T = \frac{v}{f}\)
Lời giải chi tiết:
Khoảng thời gian liên tiếp hai lần dây duỗi thẳng là nửa chu kì nên:
\(\frac{T}{2} = 0,1 \Rightarrow T = 0,2s\)
Khoảng cách giữa hai nút liên tiếp là \(\frac{\lambda }{2}\) nên ta có
\(\frac{\lambda }{2} = 5 \Rightarrow \lambda = {10_{}}cm\)
Áp dụng công thức tính bước sóng :
\(\lambda = v.T \Rightarrow v = \frac{\lambda }{T} = \frac{{10}}{{0,2}} = {50_{}}(cm/s)\)
Chọn B.
Câu hỏi 42 :
Một sợi dây căng ngang với hai đầu cố định. Trên dây đang có sóng dừng với k nút sóng kể cả hai đầu, tốc độ truyền sóng trên dây là v. Chiều dài của sợi dây là
- A \(\left( {k + 1} \right)\dfrac{v}{{2f}}\)
- B \(\left( {k - 1} \right)\dfrac{v}{{2f}}\)
- C \(k\dfrac{v}{{4f}}\)
- D \(\left( {2k + 1} \right)\dfrac{v}{{4f}}\)
Đáp án: B
Phương pháp giải:
Sử dụng biểu thức tính chiều dài sóng dừng trên dây hai đầu cố định: \(l = k\dfrac{\lambda }{2}\)
Với k = số bụng sóng = số nút sóng -1
Lời giải chi tiết:
Ta có trên dây có \(k\) nút sóng
\( \Rightarrow \) Chiều dài sóng dừng trên dây hai đầu cố định: \(l = \left( {k - 1} \right)\dfrac{\lambda }{2} = \left( {k - 1} \right)\dfrac{v}{{2f}}\)
Chọn B.
Câu hỏi 43 :
Sóng dừng trên dây với hai đầu cố định có bước sóng \(\lambda \). Khi sợi dây duỗi thẳng thì tỉ số giữa chiều dài sợi dây và bước sóng bằng
- A \(n + 0,5\) với \(n = 1,2,3...\))
- B \(n\) với \(n = 1,2,3...\))
- C \(2n\) với \(n = 1,2,3...\))
- D \(0,5n\) với \(n = 1,2,3...\))
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết về sóng dừng trên dây
Lời giải chi tiết:
Ta có sóng dừng trên dây 2 đầu cố định: \(l = \dfrac{{k\lambda }}{2}\)
\( \Rightarrow \) Khi sợi dây duỗi thẳng thì tỉ số giữa chiều dài sợi dây và bước sóng: \(\dfrac{l}{\lambda } = \dfrac{k}{2} = \dfrac{n}{2}\) với \(n = 1,2,3,...\)
Chọn D
Câu hỏi 44 :
Cho sợi dây hai đầu cố định, sóng trên dây có tốc độ không đổi. Khi sóng trên dây có tần số f thì xảy ra sóng dừng với n nút (kể cả hai đầu dây). Nếu sóng có tần số 3f thì trên dây có sóng dừng với
- A 3n bụng
- B (3n -1) bụng
- C (3n-3) bụng
- D (3n-2) bụng
Đáp án: C
Phương pháp giải:
Sử dụng biểu thức sóng dừng trên dây 2 đầu cố định: \(l = \dfrac{{k\lambda }}{2}\)
Lời giải chi tiết:
Ta có, chiều dài của dây: \(l = \dfrac{{k\lambda }}{2} = \dfrac{{kv}}{{2f}} = \left( {n - 1} \right)\dfrac{v}{{2f}}\) (2)
+ Khi sóng trên dây có tần số \(f' = 3f\) khi đó \(l = \dfrac{{mv}}{{2f'}} = m\dfrac{v}{{6f}}\) (1)
Lấy \(\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(3\left( {n - 1} \right) = m\)
\( \Rightarrow \) Số bụng khi sóng có tần số \(3f\) là \(\left( {3n - 3} \right)\) bụng.
Chọn C
Câu hỏi 45 :
Một sợi dây AB có chiều dài 60cm được căng ngang, khi sợi dây dao động với tần số 100Hz thì trên dây có sóng dừng và trong khoảng giữa A, B có 2 nút sóng. Tốc độ truyền sóng trên dây là
- A 40m/s.
- B 20m/s.
- C 40cm/s.
- D 4m/s.
Đáp án: A
Lời giải chi tiết:
Chọn đáp án A
+ Khoảng giữa AB có 2 nút sóng\( \to \)trên dây có 4 nút sóng với số bó sóng\(n = 3\).
\( \to \) Vận tốc truyền sóng trên dây\(l = 3\frac{v}{{2f}} \to v = \frac{{2lf}}{3} = \frac{{2.0,6.100}}{3} = 40\,\,{m /s}.\)
Câu hỏi 46 :
Trên một sợi dây dài 80m đang có sóng dừng ổn định, người ta đếm được 4 bó sóng. Bước sóng của sóng dừng trên dây này là
- A 20 cm
- B 160 cm
- C 40 cm
- D 80cm
Đáp án: C
Phương pháp giải:
Áp dụng điều kiện có sóng dừng trên sợi dây có hai đầu cố định
Lời giải chi tiết:
Áp dụng điều kiện có sóng dừng trên sợi dây có hai đầu cố định ta có:
\(l = k{\lambda \over 2} = > 80 = 4{\lambda \over 2} = > \lambda = 40cm\)
Câu hỏi 47 :
Một sợi dây đàn hồi có sóng dừng. Trên dây A là một bụng sóng dao động với biên độ là aA, điểm B có vị trí cân bằng cách vị trí cân bằng của của A một đoạn bằng một phần sáu bước sóng sẽ dao động với biên độ
- A \(\dfrac{{{a_A}}}{2}\)
- B \(\dfrac{{\sqrt 3 {a_A}}}{2}\)
- C \(\dfrac{{{a_A}}}{{\sqrt 2 }}\)
- D \(\dfrac{{{a_A}}}{4}\)
Đáp án: A
Phương pháp giải:
Biên độ của điểm cách bụng 1 khoảng d: \(a = {a_{bung}}.\left| {cos\dfrac{{2\pi d}}{\lambda }} \right|\)
Lời giải chi tiết:
Biên độ của B là: \({a_B} = {a_A}.\left| {cos\dfrac{{2\pi .\dfrac{\lambda }{6}}}{\lambda }} \right| = \dfrac{{{a_A}}}{2}\)
Chọn A.
Câu hỏi 48 :
Một sợi dây căng ngang, một đầu cố định, đầu còn lại gắn với cần rung của măý phát âm tần. Khi có song dừng trên dây thì tần số hiển thi trên máy phát âm tần là 20Hz. Khoảng thời gian giữa 5 lần liên tiếp sợi dây duỗi thẳng là
- A 0,1s
- B 0,5s
- C 0,25s
- D 0,2s
Đáp án: A
Lời giải chi tiết:
Hai lần duỗi thẳng liên tiếp cách nhau nửa chu kì nên 5 lần liên tiếp duỗi thẳng cách nhau 4 lần nửa chu kì tức là 2 chu kì.
\(\Delta t = 2T = 2.\frac{1}{f} = 2.\frac{1}{{20}} = 0,1s\)
Câu hỏi 49 :
Sóng dừng trên dây có phương trình u = 2Asin(25πx)sin(50πt)cm trong đó u là li độ của một điểm trên dây, x đo bằng m, t đo bằng dây. Tìm tốc độ truyền sóng?
- A 2cm/s
- B 200 cm/s
- C 4 cm/s
- D 4 m/s
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về phương trình sóng dừng
Lời giải chi tiết:
Phương trình sóng dừng u = 2Asin(25πx)sin(50πt)cm
Suy ra tần số f = 25 Hz, bước sóng 25πx = 2πx/λ => λ = 0,08 m
Do đó vận tốc truyền sóng v = λf = 0,08.25 = 2 m/s = 200 cm/s
Chọn B
Câu hỏi 50 :
Quan sát sóng dừng trên dây căng ngang, ta thấy các điểm (M, M1, M2,…) không phải là các bụng sóng cũng không phải là các nút sóng dao động với biên độ AM > 0 thì thấy các điểm này cách đều nhau nhau khoảng bằng 10 cm. Tìm bước sóng?
- A 30 cm.
- B 50 cm.
- C
40 cm.
- D 60 cm.
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết về sóng dừng, vòng tròn lượng giác
Lời giải chi tiết:
Ta có hình vẽ sau
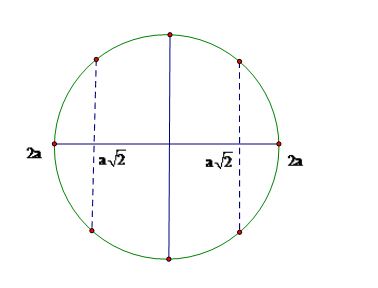
Thấy rằng những điểm có biên độ bằng nhau và cách đều nhau những khoảng 10 cm = λ/4 => λ = 40 cm
Chọn C
Tổng hợp 50 bài tập Sóng dừng mức độ vận dụng (Phần 1) được giải chi tiết giúp các em đạt điểm cao trong các kì thi
Tổng hợp 50 bài tập Sóng dừng mức độ vận dụng (Phần 2) được giải chi tiết giúp các em đạt điểm cao trong các kì thi
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng (Phần 1)
- 50 bài tập Động cơ không đồng bộ ba pha mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ nhận biết, thông hiểu
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng (Phần 1)
- 50 bài tập Động cơ không đồng bộ ba pha mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ nhận biết, thông hiểu









