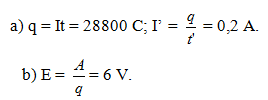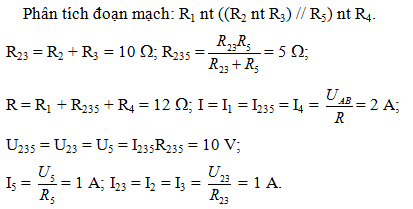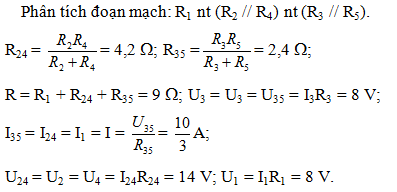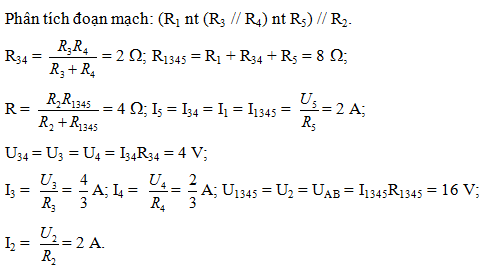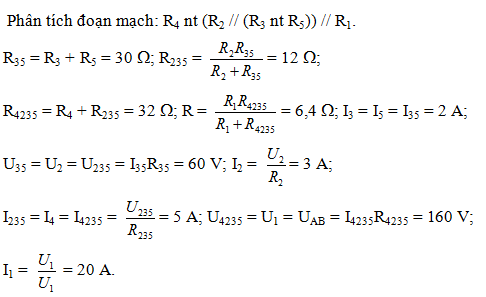30 bài tập Phương pháp giải một số bài toán về toàn mạch mức độ vận dụng (Phần 1)
Làm đề thiCâu hỏi 1 :
Một bộ acquy có thể cung cấp dòng điện 4 A liên tục trong 2 giờ thì phải nạp lại.
a) Tính cường độ dòng điện mà acquy này có thể cung cấp liên tục trong 40 giờ thì phải nạp lại.
b) Tính suất điện động của acquy này nếu trong thời gian hoạt động trên đây nó sản sinh ra một công là 172,8 kJ.
Lời giải chi tiết:
Câu hỏi 2 :
Cho đoạn mạch gồm điện trở R1 = 100Ω mắc nối tiếp với điện trở R2 = 200Ω, hiệu điện thế giữa hai đầu đoạn mạch là 12V. Hiệu điện thế giữa hai đầu điện trở R1 là:
- A U1 = 1V
- B U1 = 8V
- C U1 = 4V
- D U1 = 6V
Đáp án: C
Lời giải chi tiết:
Do hai điện trở mắc nối tiếp nên ta có: \({R_{12}} = {R_1} + {R_2} = 100 + 200 = 300\Omega = > I = {U \over {{R_{12}}}} = {{12} \over {300}} = 0,04A\)
Hiệu điện thế giữa hai đầu điện trở R1 là: \({U_1} = I.{R_1} = 0,04.100 = 4V\)
Câu hỏi 3 :
Hai bóng đèn có điện trở 5Ω mắc song song và nối vào một nguồn có điện trở trong 1Ω thì cường độ dòng điện trong mạch là 12/7 A. Khi tháo một bóng đèn ra thì cường độ dòng điện trong mạch là
- A 6/5 A.
- B 1A.
- C 5/6A.
- D 0A
Đáp án: B
Phương pháp giải:
Áp dụng định luật Ôm cho toàn mạch \(I = \frac{U}{{r + R}}\)
Lời giải chi tiết:
Hai bóng đèn giống nhau có điện trở 5 Ω mắc song song và mắc vào một nguồn có điện trở trong r = 1Ω.
Áp dụng định luật Ôm cho toàn mạch ta có
\(I = \frac{U}{{r + \frac{{R.R}}{{R + R}}}} = \frac{U}{{1 + 2,5}} = \frac{{12}}{7} = > U = \frac{{12}}{7}.3,5 = 6V\)
Khi tháo bớt một bóng đèn thì
\(I' = \frac{U}{{r + R}} = \frac{6}{{1 + 5}} = 1A\)
Câu hỏi 4 :
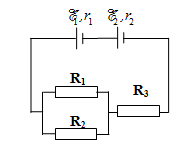
Cho mạch điện có sơ đồ như hình vẽ, trong đó suất điện động và điện trở trong của các nguồn điện tương ứng là = 1,5V, r1 = 1 ; = 3V, r2 = 2. Các điện trở ở mạch ngoài là R1 = R2 = 12 và
R3 = 1. Tính:
a) Cường độ dòng điện qua điện trở R3.
b) Công suất và hiệu suất của bộ nguồn.
Lời giải chi tiết:
Câu hỏi 5 :
Cho mạch điện như hình vẽ. Trong đó R1 = R2 = 4Ω; R3 = 6Ω; R4 = 3Ω; R5 = 10Ω; UAB = 24 V. Tính điện trở tương đương của đoạn mạch AB và cường độ dòng điện qua từng điện trở.
- A R = 6Ω; I1 = I4 = 1A; I2 = I3 = I5 = 2A
- B R = 6Ω; I1 = I4 = 2A; I2 = I3 = I5 = 1A
- C R = 12Ω; I1 = I4 = 2A; I2 = I3 = I5 = 2A
- D R = 12Ω; I1 = I4 = 2A; I2 = I3 = I5 = 1A
Đáp án: D
Lời giải chi tiết:
Chọn D
Câu hỏi 6 :
Cho mạch điện như hình vẽ. Trong đó R1 = R3 = R5 = 3Ω; R2 = 8Ω; R4 = 6Ω; U5 = 6 V. Tính điện trở tương đương của đoạn mạch AB và cường độ dòng điện chạy qua từng điện trở.
- A \(R = 4\Omega ;{I_1} = {I_5} = 2A;{I_3} = {4 \over 3}A;{I_4} = {2 \over 3}A;{I_2} = 2A\)
- B \(R = 8\Omega ;{I_1} = {I_5} = 2A;{I_3} = {4 \over 3}A;{I_4} = {2 \over 3}A;{I_2} = 2A\)
- C \(R = 4\Omega ;{I_1} = {I_5} = 1A;{I_3} = {4 \over 3}A;{I_4} = {2 \over 3}A;{I_2} = 2A\)
- D \(R = 8\Omega ;{I_1} = {I_5} = 2A;{I_3} = {2 \over 3}A;{I_4} = {4 \over 3}A;{I_2} = 2A\)
Đáp án: A
Lời giải chi tiết:
Chọn A
Câu hỏi 7 :
Cho mạch điện như hình vẽ. Trong đó R1 = 8Ω; R3 = 10Ω; R2 = R4 = R5 = 20Ω; I3 = 2 A. Tính điện trở tương đương của đoạn mạch AB và cường độ dòng điện trên từng điện trở.
- A \(R = 32\Omega ;{I_1} = 4A;{I_2} = 3A;{I_3} = {I_5} = 2A;{I_4} = 5A\)
- B \(R = 32\Omega ;{I_1} = 20A;{I_2} = 3A;{I_3} = {I_5} = 2A;{I_4} = 5A\)
- C \(R = 6,4\Omega ;{I_1} = 20A;{I_2} = 3A;{I_3} = {I_5} = 2A;{I_4} = 5A\)
- D \(R = 6,4\Omega ;{I_1} = 4A;{I_2} = 3A;{I_3} = {I_5} = 2A;{I_4} = 5A\)
Đáp án: C
Lời giải chi tiết:
CChọn C
Câu hỏi 8 :
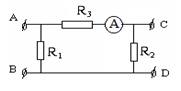
Cho mạch điện như hình vẽ.
Nếu đặt vào AB hiệu điện thế 100 V thì người ta có thể lấy ra ở hai đầu CD một hiệu điện thế UCD = 40 V và ampe kế chỉ 1A.
Nếu đặt vào CD hiệu điện thế 60 V thì người ta có thể lấy ra ở hai đầu AB hiệu điện thế UAB = 15 V. Coi điện trở của ampe kế không đáng kể. Tính giá trị của mỗi điện trở.
- A \({R_1} = 30\Omega ;{R_2} = 40\Omega ;{R_3} = 50\Omega \)
- B \({R_1} = 20\Omega ;{R_2} = 40\Omega ;{R_3} = 60\Omega \)
- C \({R_1} = 20\Omega ;{R_2} = 30\Omega ;{R_3} = 40\Omega \)
- D \({R_1} = 30\Omega ;{R_2} = 40\Omega ;{R_3} = 60\Omega \)
Đáp án: B
Lời giải chi tiết:
chọn B
Câu hỏi 9 :
Cho mạch điện như hình vẽ.
Biết R3 = R4.
Nếu nối hai đầu AB vào hiệu điện thế 120 V thì cường độ dòng điện qua R2 là 2 A và UCD = 30 V.
Nếu nối 2 đầu CD vào hiệu điện thế 120 V thì UAB = 20 V.
Tính giá trị của mỗi điện trở.
- A \({R_1} = 20\Omega ;{R_2} = 40\Omega ;{R_3} = 30\Omega \)
- B \({R_1} = 20\Omega ;{R_2} = 40\Omega ;{R_3} = 60\Omega \)
- C \({R_1} = 30\Omega ;{R_2} = 40\Omega ;{R_3} = 60\Omega \)
- D \({R_1} = 20\Omega ;{R_2} = 50\Omega ;{R_3} = 60\Omega \)
Đáp án: B
Lời giải chi tiết:
bChọn B
Câu hỏi 11 :
Cho mạch điện như hình vẽ. Trong đó R1 = 2,4Ω; R3 = 4Ω; R2 = 14Ω; R4 = R5 = 6Ω; I3 = 2 A. Tính điện trở tương đương của đoạn mạch AB và hiệu điện thế giữa hai đầu các điện trở.
- A R = 12Ω; U2 = U4 = 8V; U1 = 8V; U3 = U5 = 14V
- B R = 12Ω; U2 = U4 = 14V; U1 = 6V; U3 = U5 = 8V
- C R = 12Ω; U2 = U4 = 14V; U1 = 4V; U3 = U5 = 8V
- D R = 9Ω; U2 = U4 = 14V; U1 = U3 = U5 = 8V
Đáp án: D
Lời giải chi tiết:
Chọn D
Câu hỏi 12 :
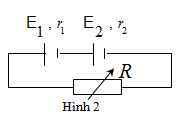
Cho mạch điện như hình vẽ 2
Bộ nguồn có hai nguồn: E = 1,5 V; r1 = 0,25 Ω; và = 4,5 V;
r2 = 0,75 Ω; R là biến trở.
a) Tính suất điện động và điện trở trong của bộ nguồn.
b) Tính cường độ dòng điện chạy qua mạch chính khi R = 2 Ω.
c) Tìm giá trị của R để công suất tiêu thụ của biến trở R đạt giá trị cực đại
Lời giải chi tiết:
Câu hỏi 13 :
Đặt vào hai đầu đoạn chứa biến trở R một nguồn điện 1 chiều ξ = 20 V và điện trở trong r. Thay đổi giá trị của biến trở thì thấy khi R1 = 2 Ω và R2 = 12,5 Ω thì giá trị công suất của mạch là như nhau. Công suất tiêu thụ cực đại trên mạch là
- A 10 W.
- B 30 W.
- C 40 W
- D 20 W.
Đáp án: C
Phương pháp giải:
Phương pháp: Áp dụng công thức tính công suất tiêu thụ của toàn mạch
$$P = {I^2}\left( {R + r} \right) = {{{\xi ^2}R} \over {{{\left( {R + r} \right)}^2}}} = {{{\xi ^2}R} \over {{R^2} + 2{\rm{Rr}} + {r^2}}}.$$
Lời giải chi tiết:
Đáp án C
+ Công suất tiêu thụ trên mạch $$P = {I^2}\left( {R + r} \right) = {{{\xi ^2}R} \over {{{\left( {R + r} \right)}^2}}} = {{{\xi ^2}R} \over {{R^2} + 2{\rm{Rr}} + {r^2}}}.$$
Ta thu được phương trình bậc hai với ẩn R: $${{\rm{R}}^2} - \left( {{{{\xi ^2}} \over P} - 2{{r}}} \right)R + {r^2} = 0.$$ Phương trình cho ta hai nghiệm thỏa mãn $${{\rm{R}}_1}{R_2} = {r^2} \Rightarrow r = 5\,\Omega .$$
+ Mặt khác$$P = {{{\xi ^2}R} \over {{R^2} + 2{\rm{Rr}} + {r^2}}} = {{{\xi ^2}} \over {R + {{{r^2}} \over R} + 2{\rm{r}}}} \to {P_{\max }}$$khi R = r và $${P_{\max }} = {{{\xi ^2}} \over {2r}} = 40\,\,W.$$
Câu hỏi 14 :
Cho mạch điện có sơ đồ như hình bên:
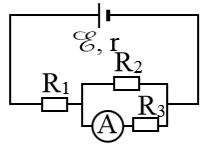
E = 12 V; R1 = 4 Ω; R2 = R3 = 10 Ω. Bỏ qua điện trở của ampe kế A và dây nối. Số chỉ của ampe kế là 0,6 A. Giá trị điện trở trong r của nguồn điện là
- A 1,2 Ω.
- B 0,5 Ω.
- C 1,0 Ω.
- D 0,6 Ω.
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính hiệu điện thế, cường độ dòng điện và điện trở tương của của đoạn mạch mắc nối tiếp và song song
Sử dụng biểu thức định luật Ôm cho toàn mạch: I = E/(r + RN)
Lời giải chi tiết:
Từ sơ đồ mạch điện ta có (R3//R2) ntR1
Hiệu điện thế của U3 là : \({U_3} = {I_A}.{R_3} = 0,6.10 = 6V\)
Do R3 // R2 nên ta có U2 = U3= 6V
Cường độ dòng điện qua R2 là: \({I_2} = {{{U_2}} \over {{R_2}}} = {6 \over {10}} = 0,6V\)
Cường độ dòng điện chạy trong mạch là I = I3 + I2 = 0,6 + 0,6 = 1,2A
Điện trở toàn mạch là: \({R_b} = {R_1} + {{{R_2}.{R_3}} \over {{R_2} + {R_3}}} = 4 + {{10.10} \over {10 + 10}} = 9\Omega \)
Áp dụng định luật Ohm cho toàn mạch ta có : \(I = {\zeta \over {r + {R_b}}} \Rightarrow 1,2 = {{12} \over {r + 9}} \Rightarrow r = 1\Omega \)
Câu hỏi 15 :
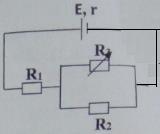
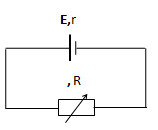
Cho sơ đồ mạch điện như hình vẽ: r = 2Ω, R1 = 4Ω, R2 = 6Ω, R3 là một biến trở. Thay đổi biến trở R3 đến giá trị nào thì công suất trên R3 đạt giá trị cực đại
- A 1Ω
- B 3Ω.
- C 4Ω.
- D 2Ω
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính công suất tỏa nhiệt trên điện trở, bất đẳng thức Cô-si
Lời giải chi tiết:
Cường độ dòng điện trong mạch kín được tính theo công thức
\(I = \frac{E}{{{R_1} + \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} + r}} = \frac{E}{{6 + \frac{{6{R_3}}}{{6 + {R_3}}}}} = \frac{{E\left( {{R_3} + 6} \right)}}{{12{R_3} + 36}}\)
Ta có \({U_{23}} = I{R_{23}} = \frac{{E\left( {{R_3} + 6} \right)}}{{12{R_3} + 36}}.\frac{{6{R_3}}}{{{R_3} + 6}} = \frac{{E.6{R_3}}}{{12{R_3} + 36}}\)
Công suất tỏa nhiệt trên điện trở R3 được tính theo công thức
\[{P_3} = \frac{{U_3^2}}{{{R_3}}} = \frac{{U_{23}^2}}{{{R_3}}} = \frac{{{{\left( {\frac{{E.6{R_3}}}{{12{R_3} + 36}}} \right)}^2}}}{{{R_3}}} = \frac{{36E{R_3}}}{{{{\left( {12 + 36{R_3}} \right)}^2}}} = \frac{{3E}}{{12{{\left( {\frac{1}{{\sqrt {{R_3}} }} + 3\sqrt {{R_3}} } \right)}^2}}}\]
Để P3max thì \[{\left( {\frac{1}{{\sqrt {{R_3}} }} + 3\sqrt {{R_3}} } \right)_{\min }} \Rightarrow \frac{1}{{\sqrt {{R_3}} }} = 3\sqrt {{R_3}} \](theo bất đẳng thức Cô-si)
Suy ra R3 = 3Ω
Chọn B
Câu hỏi 16 :
Cho mạch điện gồm R1 = 5Ω, ampe kế và dây nối có điện trở nhỏ, vôn kế có điện trở rất lớn, suất điện động của nguồn E = 3V, điện trở trong r, ampe kế chỉ 0,3A và vôn kế chỉ 1,2V. Tìm điện trở trong r?
- A 0,5Ω
- B 1Ω
- C 0,75 Ω
- D 0,25 Ω
Đáp án: B
Phương pháp giải:
Sử dụng công thức định luật Ôm cho toàn mạch
Lời giải chi tiết:
Số chỉ ampe kế chính là cường độ dòng điện trong mạch chính I = 0,3 A
Vì R1 nt R2 nên I1 = I2 = I = 0,3A
Số chỉ vôn kế là hiệu điện thế hai đầu điện trở R2
U2 = UV = 1,2V
Điện trở R2 được xác định theo công thức R2 = U2/I2 = 4Ω
Điện trở tương đương của đoạn mạch RTD = R1 + R2 = 9Ω
Áp dụng biểu thức định luật Ôm cho toàn mạch ta có
\(I = {E \over {{R_{TD}} + r}} \Rightarrow r = {E \over I} - {R_{TD}} = {3 \over {0,3}} - 9 = 1\Omega \)
Chọn B
Câu hỏi 17 :
Một nguồn điện có suất điện động E = 12 V và điện trở trong 2 Ω. Nối điện trở R vào hai cực của nguồn điện thành mạch kín thì công suất tiêu thụ điện trên điện trở R bằng 16 W. Biết R > 2 Ω, giá tri của điện trở R bằng
- A 3 Ω.
- B 6 Ω.
- C 5 Ω.
- D 4 Ω.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Ta có
\(\eqalign{
& P = {I^2}R = \left( {{E \over {R + r}}} \right)R = > {R^2} + 2rR + {r^2} = {{{E^2}} \over P}R = > {R^2} + \left( {2r - {{{E^2}} \over P}} \right)R + r = 0 \cr
& = > {R^2} + \left( {2.2 - {{{{12}^2}} \over {16}}} \right)R + {2^2} = 0 = > \left\{ \matrix{
R = 4\Omega \hfill \cr
R = 1\Omega \hfill \cr} \right. \cr} \)
Câu hỏi 18 :
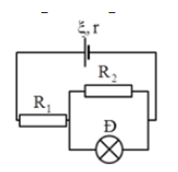
Cho mạch điện có sơ đồ như hình vẽ: ξ = 12 V; R1 = 5 Ω; R2 = 12 Ω; bóng đèn Đ: 6 V – 3 W. Bỏ qua điện trở các dây nối. Để đèn sáng bình thường thì điện trở trong r của nguồn có giá trị
- A 1 Ω.
- B 2 Ω.
- C 5 Ω.
- D 5,7 Ω.
Đáp án: A
Phương pháp giải:
Áp dụng công thức tính cồng suất của dòng điện
Lời giải chi tiết:
Đáp án A.
+ Điện trở và cường độ dòng điện định mức của đèn
\({{\rm{R}}_d} = {{{\rm{U}}_d^2} \over {{{\rm{P}}_d}}} = {{{6^2}} \over 3} = 12\Omega ;{\rm{ }}{{\rm{I}}_d} = {{{{\rm{P}}_d}} \over {{{\rm{U}}_d}}} = {3 \over 6} = 0,5{\rm{A}}{\rm{.}}\)
Cường độ dòng điện qua \({{\rm{I}}_2}{\rm{:}}{{\rm{I}}_2} = {{{{\rm{U}}_{\rm{d}}}} \over {{{\rm{P}}_2}}} = {6 \over {12}} = 0,5{\rm{A}} \to {{\rm{I}}_{\rm{m}}} = 1{\rm{A}}{\rm{.}}\)
+ Cường độ dòng điện qua mạch \({{\rm{I}}_{\rm{m}}} = {\xi \over {{{\rm{R}}_{\rm{N}}} + {\rm{r}}}} \leftrightarrow 1 = {{12} \over {5 + {{12.12} \over {12 + 12}} + {\rm{r}}}} \to {\rm{r = 1}}\Omega {\rm{.}}\)
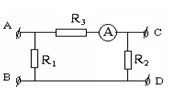
Câu hỏi 19 :
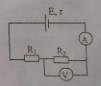
Cho mạch điện có sơ đồ như hình vẽ: \(r = 1,5\Omega ;{R_1} = {R_3} = 10\Omega ;{R_2} = 5\Omega \).Bỏ qua điện trở của ampe kế và dây nối. Số chỉ của ampe kế là 1,2 A.Công suất của nguồn điện là
- A 24 W.
- B 30 W.
- C 18 W.
- D 37,5 W.
Đáp án: B
Phương pháp giải:
Áp dụng định luật Ohm cho toàn mạch và công thức tính công suất của toản mạch
Lời giải chi tiết:
Đáp án B
\(\left\{ \begin{array}{l}{U_{AB}} = {R_3}{I_A} = 12V = > {I_1} = {I_2} = \frac{{{R_3}{I_A}}}{{{R_{12}}}} = > I = {I_A} + \frac{{{R_3}{I_A}}}{{{R_{12}}}} = 2A\\{U_{AB}} = \xi - Ir = > \xi = 15V = > {P_{nguon}} = \xi I = (12 + 2.1,5).2 = 30W\end{array} \right.\)
Câu hỏi 20 :
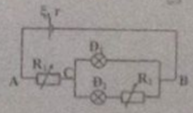
Cho mạch điện như hình vẽ. Biết \(E = 6,6V;r = 0,12\Omega \). Đèn Đ1 loại 6V-3W; đèn Đ2 loại 2,5V-1,25W. Điều chỉnh R1 và R2 sao cho hai đèn sáng bình thường. Giá trị của R2 là
- A 7Ω
- B 6Ω
- C 8Ω
- D 5Ω
Đáp án: A
Phương pháp giải:
Biểu thức cường độ âm I = U/R
Lời giải chi tiết:
Cường độ dòng điện qua đèn 2: \({I_2} = {P_2}:{U_2} = 0,5A\)
Hiệu điện thế hai đầu R2 là: \({U_{{R_2}}} = {U_{{D_1}}} - {U_{{D_2}}} = 6 - 2,5 = 3,5\)
Giá trị điện trở R2 là: \({R_2} = {{{U_2}} \over {{I_2}}} = 7\Omega \)
Câu hỏi 21 :
Cho mạch điện như hình vẽ. Biết suất điện động của nguồn ξ = 12 V, điện trở trong r = 1 Ω, mạch ngoài gồm điện trở R1 = 3 Ω, R2 = 6 Ω, R3 = 5 Ω. Hiệu điện thế giữa hai đầu điện trở R2 là
- A 3,5 V.
- B 4,8 V.
- C 2,5 V.
- D 4.5 V.
Đáp án: B
Lời giải chi tiết:
Đáp án B
+ Hiệu điện thế U2 giữa hai đầu điện trở R2 :
\({U_2} = I{R_2} = {{\xi {R_2}} \over {{R_1} + {R_2} + {R_3} + r}} = {{12.6} \over {3 + 6 + 5 + 1}} = 4,8V.\)
Câu hỏi 22 :
Cho mạch điện như hình vẽ. Trong đó, nguồn điện có suất điện động E, điện trở trong r = 2 Ω ; mạch ngoài là biến trở R. Thay đổi giá trị của biến trở và đo công suất tỏa nhiệt trên biến trở thì thấy có những cặp giá trị R1 và R2 ứng với cùng một công suất. Một trong những cặp giá trị đó có R1 = 1Ω ; giá trị R2 bằng
- A 2Ω.
- B 3Ω.
- C 4Ω.
- D 5Ω.
Đáp án: C
Lời giải chi tiết:
Đáp án C
Khi công suất mạch ngoài cực đại thì có hai giá trị của biến trở thỏa mãn điều kiện R1 .R2 = r2 .Với R1 = 1Ω thì R2 = 4Ω.
Câu hỏi 23 :
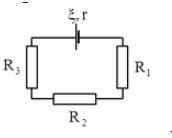
Cho mạch điện như hình vẽ. Các điện trở có giá trị bằng nhau R = 6 Ω. Nguồn điện có suất điện động ɛ = 3 V, điện trở trong r = 2 Ω. Điện trở của các dây nối và khoá K không đáng kể. Cường độ dòng điện chạy qua nguồn khi đóng khoá K có giá trị bằng
- A 1,5 (A).
- B 0,75(A).
- C 0,15 (A).
- D 0,6(A).
Đáp án: D
Lời giải chi tiết:
Đáp án D
Khi khóa k đóng ta có điện trở mạch ngoài được xác định bởi biểu thức \({R_{td}} = \frac{R}{2} = 3\Omega \)
Áp dụng định luật Ohm cho toàn mạch ta xác định được cường độ dòng điện chạy qua mạch là
\(I = \frac{\xi }{{{R_{td}} + r}} = \frac{3}{{3 + 2}} = 0,6A\)
Câu hỏi 26 :
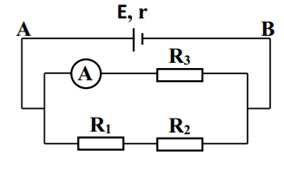
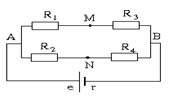
Cho mạch điện như hình vẽ. Trong đó R1 = R3 = R5 = 3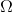 
; R2 = 8 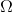; R4 = 6 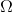; U5 = 6 V. Tính điện trở tương đương của đoạn mạch AB và cường độ dòng điện chạy qua từng điện trở
Lời giải chi tiết:
Câu hỏi 27 :
Cho mạch điện như hình vẽ. Trong đó R1 = 8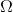 
; R3 = 10 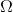; R2 = R4 = R5 = 20 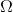; I3 = 2 A.
Tính điện trở tương đương của đoạn mạch AB, hiệu điện thế và cường độ dòng điện trên từng điện trở
Lời giải chi tiết:
Câu hỏi 28 :
Cho mạch điện như hình vẽ.
Nếu đặt vào AB hiệu điện thế 100 V thì người ta có thể lấy ra ở hai đầu CD một hiệu điện thế UCD = 40 V và ampe kế chỉ 1A.
Nếu đặt vào CD hiệu điện thế 60 V thì người ta có thể lấy ra ở hai đầu AB hiệu điện thế UAB = 15 V. Coi điện trở của ampe kế không đáng kể. Tính giá trị của mỗi điện trở.
Lời giải chi tiết:
Câu hỏi 29 :
Cho mạch điện như hình vẽ.
Biết R3 = R4.
Nếu nối hai đầu AB vào hiệu điện thế 120 V thì cường độ dòng điện qua R2 là 2 A và UCD = 30 V.
Nếu nối 2 đầu CD vào hiệu điện thế 120 V thì UAB = 20 V.
Tính giá trị của mỗi điện trở.
Lời giải chi tiết:
Câu hỏi 30 :
Cho mạch điện như hình vẽ. Trong đó E = 48 V; r = 2 \(\Omega \); R1 = 2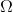 
; R2 = 8 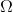; R3 = 6 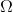; R4 = 16 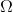. Điện trở của các dây nối không đáng kể. Tính hiệu điện thế giữa hai điểm M và N. Muốn đo UMN phải mắc cực dương của vôn kế với điểm nào?
Lời giải chi tiết:
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- 40 bài tập Dòng điện trong chân không mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất khí mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất điện phân mức độ vận dụng
- 40 bài tập Dòng điện trong chất điện phân mức độ nhận biết, thông hiểu
- 40 bài tập dòng điện trong kim loại mức độ vận dụng
- 50 bài tập Định luật Ôm đối với toàn mạch mức độ vận dụng (Phần 2)
- 40 bài tập Dòng điện trong chân không mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất khí mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất điện phân mức độ vận dụng
- 40 bài tập Dòng điện trong chất điện phân mức độ nhận biết, thông hiểu
