Đề kiểm tra 45 phút (1 tiết) - Chương 2, 3 - Đề số 2 - Đại số 10

Đề bài

Câu 1. Cho hàm số \(y = 2mx + 1 - m{\rm{ }}(1)\) .

a.Lập bảng biến thiên và vẽ đồ thị hàm số (1) khi \(m= -1.\)

b.Tìm điểm cố định mà đồ thị hàm số (1) luôn đi qua khi m thay đổi.

c.Tìm m để đồ thị hàm số (1) cắt parabol \(y = {x^2} + 2x - 2\) tại hai điểm phân biệt.

Câu 2.

a.Giải phương trình \(\left( {{x^2} + x - 2} \right)\left( {{x^2} + x - 3} \right) = 12\) .

b.Giải và biện luận phương trình \(\dfrac{{x - m}}{{x - 1}} = {m^2}\) theo tham số m.

Câu 3. Cho phương trình \(m{x^2} - 2\left( {m + 1} \right)x + m + 2 = 0\) .

a. Xác định m để phương trình có một nghiệm bằng 2. Tìm nghiệm còn lại.

b. Xác định các giá trị nguyên của m để phương trình có hai nghiệm phân biệt sao cho tổng các nghiệm là một số nguyên.

Lời giải chi tiết

Câu 1.

a. Khi \(m= -1\) ta có hàm số \(y =  - 2x + 2\) .

Tập xác định D=R.

Do a=-2 < 0 nên hàm số nghịch biến trên R.

\(x = 0 \Rightarrow y = 2\) : Đồ thị cắt trục tung tại điểm (0;2).

\(y = 0 \Rightarrow x = 1\) : Đồ thị cắt trục hoành tại điểm (1;0).

Đồ thị

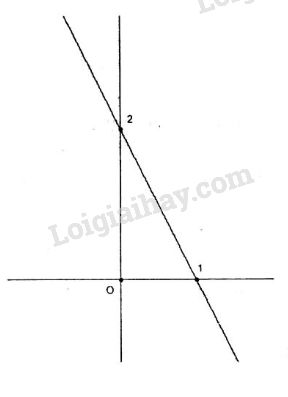
b. Giả sử \(\left( {{x_0};{y_0}} \right)\) là điểm đồ thị luôn luôn đi qua khi m thay đổi.

Ta có:

\(\begin{array}{l}
{y_0} = 2m{x_0} + 1 - m\\
\Leftrightarrow 2m{x_0} - m + 1 - {y_0} = 0\\
\Leftrightarrow \left( {2{x_0} - 1} \right)m + \left( {1 - {y_0}} \right) = 0
\end{array}\)

Điểm M là điểm cố định mà đồ thị hàm số luôn đi qua

\(\Leftrightarrow \) phương trình trên nghiệm đúng với mọi m

\(\Leftrightarrow  \left\{ \matrix{  2{x_0} - 1 = 0 \hfill \cr  1 - {y_0} = 0 \hfill \cr}  \right. \)

\(\Leftrightarrow \left\{ \matrix{  {x_0} = {1 \over 2} \hfill \cr  {y_0} = 1 \hfill \cr}  \right.\)

Vậy đồ thị luôn luôn đi qua điểm \(\left( {\dfrac{1}{2};1} \right)\) khi m thay đổi.

c. Phương trình hoành độ giao điểm parabol và đường thẳng

\({x^2} + 2x - 2 = 2mx + 1 - m\)

\(\Leftrightarrow {x^2} + 2\left( {1 - m} \right)x + m - 3 = 0(*)\)

Đường thẳng cắt Parabol tại hai điểm phân biệt \(\Leftrightarrow (*)\) có hai nghiệm phân biệt.

Ta có:

\(\Delta ' = {\left( {1 - m} \right)^2} - \left( {m - 3} \right)\)\(\, = {m^2} - 3m + 4 \)\(\,= {\left( {m - \dfrac{3}{2}} \right)^2} + \dfrac{7}{4} > 0,\,\forall m \in \mathbb{R}\)

Suy ra đường thẳng luôn luôn cắt parabol tại hai điểm phân biệt với mọi m.

Câu 2.

a. Xét phương trình \(\left( {{x^2} + x - 2} \right)\left( {{x^2} + x - 3} \right) = 12\)

Đặt \(t = {x^2} + x - 2\) .Phương trình trở thành

\(t\left( {t - 1} \right) = 12 \Leftrightarrow {t^2} - t - 12 = 0\)

\(\Leftrightarrow \left[ \matrix{  t = 4 \hfill \cr  t =  - 3 \hfill \cr}  \right.\)

Với: \({x^2} + x - 2 = 4 \Leftrightarrow {x^2} + x - 6 = 0 \)

\(\Leftrightarrow \left[ \matrix{  x =  - 3 \hfill \cr  x = 2 \hfill \cr}  \right.\)

Với: \({x^2} + x - 2 =  - 3 \Leftrightarrow {x^2} + x + 1 = 0\) . Phương trình vô nghiệm.

Kết luận: Phương trình đã cho có hai nghiệm \(x= -3, x= 2.\)

b. Xét phương trình \(\dfrac{{x - m}}{{x - 1}} = {m^2}\)  (1)

Điều kiện xác định: \(x \ne 1\) .

Với điều kiện trên phương trình tương đương

\(x - m = {m^2}\left( {x - 1} \right) \)

\(\begin{array}{l}
\Leftrightarrow x - m = {m^2}x - {m^2}\\
\Leftrightarrow {m^2}x - x = {m^2} - m
\end{array}\)

\(\Leftrightarrow \left( {{m^2} - 1} \right)x = {m^2} - m\)    (2)

Với \({m^2} - 1 \ne 0 \Leftrightarrow m \ne  \pm 1\) : Phương trình (2) có nghiệm duy nhất

\(x = \dfrac{{{m^2} - m}}{{{m^2} - 1}}  = \frac{{m\left( {m - 1} \right)}}{{\left( {m - 1} \right)\left( {m + 1} \right)}}= \dfrac{m}{{m - 1}}\)

Nghiệm này thỏa mãn điều kiện \(x \ne 1\) .

Với: \({m^2} - 1 = 0 \Leftrightarrow m =  \pm 1\)

+)  \(m= 1\) phương trình (2) trở thành \(0x= 0\). Phương trình nghiệm đúng với mọi \(x\in R\).

Suy ra phương trình (1) nghiệm đúng với mọi \(x \ne 1\) .

+) \(m= -1\) phương trình (2) trở thành \(0x= 2\). Phương trình vô nghiệm.

Suy ra phương trình (1) vô nghiệm.

Kết luận:

\(m \ne  \pm 1:x = \dfrac{m}{{m - 1}}\)

\(m = 1:x \ne 1\)

\(m =  - 1\) : Vô nghiệm

Câu 3.

a. Xét phương trình \(m{x^2} - 2\left( {m + 1} \right)x + m + 2 = 0\).

Phương trình có nghiệm x= 2 khi: \(4m - 4\left( {m + 1} \right) + m + 2 = 0\)

\(\begin{array}{l}
\Leftrightarrow 4m - 4m - 4 + m + 2 = 0\\
\Leftrightarrow m - 2 = 0
\end{array}\)

\(\Leftrightarrow m = 2\) .

Khi đó phương trình trở thành \(2{x^2} - 6x + 4 = 0\)

\(\Leftrightarrow \left[ \matrix{  x = 2 \hfill \cr  x = 1 \hfill \cr}  \right.\)

Vậy phương trình có nghiệm \(x= 2\) khi \(m= 2\). Nghiệm còn lại là \(x= 1\).

b. Ta có:

\(\Delta ' = {\left( {m + 1} \right)^2} - m\left( {m + 2} \right) = 1 > 0\) .

Suy ra phương trình luôn có hai nghiệm phân biệt với \(\forall m \ne 0\) .

Khi đó tổng các nghiệm là: \(S = \dfrac{{2\left( {m + 1} \right)}}{m} = \dfrac{{2m + 2}}{m}= 2 + \dfrac{2}{m}\).

S là số nguyên khi và chỉ khi m là ước số của 2.

Vậy \(m =  \pm 1,m =  \pm 2\) .

 Loigiaihay.com