 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề kiểm tra 15 phút – Chương 2 – Đại số 10
Đề kiểm tra 15 phút – Chương 2 – Đại số 10
Đề kiểm tra 15 phút - Chương 2 - Đề số 2 - Đại số 10
Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Đề số 5 - Đại số 10
Đề bài
Câu hỏi trắc nghiệm 100%
Chọn phương án đúng
Câu 1. Tập xác định của hàm số \(y = \dfrac{{2x - {x^2}}}{{{x^2} + 1}}\) là
A.\(\mathbb{R}\)
B.\(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\)
C.\(\mathbb{R}\backslash \left\{ 1 \right\}\)
D.\(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
Câu 2.Tập xác định của hàm số
\(y = \left\{ \begin{array}{l}
1 - x{\;\rm{ khi }} - 2 \le x < - 1\\
3x + 2{\;\rm{ khi }} - 1 \le x < 1\\
2x + 3{\;\rm{ khi }}1 < x < 3
\end{array} \right.\)
là
A.\(\left[ { - 2;3} \right]\)
B. \(\left( { - 2;3} \right)\)
C. \(\left[ { - 2;3} \right)\)
D.\(\left( { - 2;3} \right]\)
Câu 3. Cho hàm số \(f(x) = \left| {2x - 1} \right|\) . Lúc đó \(f\left( x \right) = 3\) khi
A. \(x=2\)
B. \(x=2\) hoặc \(x=-1\)
C. \(x = \pm 2\)
D. Kết quả khác
Câu 4. Điểm nào sau đây thuộc đồ thị hàm số \(y = \dfrac{{x - 1}}{{2{x^2} - 3x + 1}}\) ?
A.\(A\left( {0;1} \right)\)
B.\(B\left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\)
C.\(C\left( {1;0} \right)\)
D.\(D\left( {2;\dfrac{1}{3}} \right)\)
Câu 5. Cho hàm số \(\;f\left( x \right) = {\rm{ }}2{x^3}\;-{\rm{ }}3x{\rm{ }} + {\rm{ }}1\). Tìm mệnh đề đúng
A. \(f\left( x \right)\) là hàm chẵn
B. \(f\left( x \right)\) là hàm lẻ
C. \(f\left( x \right)\) là hàm không chẵn, không lẻ
D. \(f\left( x \right)\) là hàm vừa chẵn, vừa lẻ
Câu 6. Trong các hàm số sau, hàm số nào là hàm lẻ ?
A. \(y = \left| {x - 2} \right| + \left| {x + 2} \right|\)
B. \(y = \left| {x - 2} \right| - \left| {x + 2} \right|\)
C. \(y = \left| {1 - 2x} \right| + \left| {1 + 2x} \right|\)
D. \(y = \left| {{x^2} - 4} \right|\)
Câu 7. Trong các hàm số sau, hàm số nào không phải là hàm chẵn ?
A. \(y = - {x^{4\;}}{\rm{ + }}3\)
B. \(y = \dfrac{1}{{{x^4}}}\)
C. \(y = {x^{4\;}} + 3{x^{2\;}} - 2\)
D. \(y = {x^2} - 3x\)
Câu 8. Tịnh tiến đồ thị hàm số \(y = 2x{\rm{ }} - 3\) sang phải 2 đơn vị, rồi xuông dưới 1 đơn vị thì đồ thị hàm số
A.\(y = 2x + 2\)
B. \(y = 2x-6\)
C. \(y = 2x-8\)
D. \(y = 2x\)
Câu 9. Một đường thẳng song song với đường thẳng \(y = - x\sqrt 2 \) là
A. \(y + x\sqrt 2 = 2\)
B. \(y = - \dfrac{1}{{\sqrt 2 }}x - 2\)
C.\(y = x\sqrt 2 + 2\)
D.\(y - \dfrac{2}{{\sqrt 2 }}x = - 2\)
Câu 10. Đồ thị trên Hình 1 là hàm số
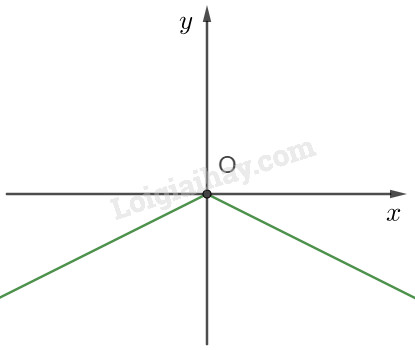
A. \(y = \left| x \right|\)
B. \(y = 2\left| x \right| - 2\)
C. \(y = \dfrac{1}{2}\left| x \right|\)
D. \(y = - \dfrac{1}{2}\left| x \right|\)
Lời giải chi tiết
Câu 1. Chọn A
Do \({x^2} + 1 \ne 0\forall x \in \mathbb{R}\) nên hàm số có tập xác định là \(D = \mathbb{R}\) .
Câu 2. Chọn C
Tập xác định của hàm số là \(D = \left[ { - 2; - 1} \right) \cup \left[ { - 1;1} \right] \cup \left( {1;3} \right) \)\(\;= \left[ { - 2;3} \right)\) .
Câu 3. Chọn B
\(\begin{array}{l}f\left( x \right) = 3 \Leftrightarrow \left| {2x - 1} \right| = 3\\{\rm{ }} \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 3\\2x - 1 = - 3\end{array} \right.\\{\rm{ }} \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 1\end{array} \right.\end{array}\)
Câu 4. Chọn D
Hàm số \(y = \dfrac{{x - 1}}{{2{x^2} - 3x + 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ {1;\dfrac{1}{2}} \right\}\)
Gọi (G) là đồ thị hàm số.
+ \(f\left( 0 \right) = - 1 \ne 1 \Rightarrow A \notin \left( G \right)\) .
+ \(\dfrac{1}{2} \notin D \Rightarrow B \notin \left( G \right)\).
+ \(1 \notin \mathbb{R} \Rightarrow C \notin \mathbb{R}\).
+ \(f\left( 2 \right) = \dfrac{1}{3} \Rightarrow D \in \left( G \right)\).
Câu 5. Chọn C
Hàm số \(f\left( x \right) = {\rm{ }}2{x^3}\;-{\rm{ }}3x{\rm{ }} + {\rm{ }}1\) có tập xác định \(D = \mathbb{R}\) là tập đối xứng.
Ta có \(f\left( 1 \right){\rm{ }} = {\rm{ }}0,{\rm{ }}f\left( { - 1} \right){\rm{ }} = {\rm{ }}2\).
Suy ra \(f\left( { - 1} \right) \ne f\left( 1 \right),f\left( { - 1} \right) \ne - f\left( 1 \right)\) .
Vậy hàm số không chẵn cũng không lẻ.
Câu 6. Chọn B
Xét hàm \(f\left( x \right) = \left| {x - 2} \right| - \left| {x + 2} \right|\).
Hàm số có tập xác định \(D = \mathbb{R}\) là tập đối xứng.
Ta có \(\begin{array}{l}f( - x) = \left| { - x - 2} \right| - \left| { - x + 2} \right|\\{\rm{ }} = \left| { - \left( {x + 2} \right)} \right| - \left| { - \left( {x - 2} \right)} \right|\\{\rm{ }} = \left| {x + 2} \right| - \left| {x - 2} \right| = - f\left( x \right)\end{array}\).
Suy ra \(f\left( x \right)\) là hàm số lẻ.
Câu 7. Chọn D.
Xét hàm số \(f\left( x \right) = {x^2} - 3x\) .
Ta có\(f\left( 1 \right) = 2,f\left( { - 1} \right) = 4\) .
Suy ra \(f\left( { - 1} \right) \ne f\left( 1 \right)\) . Vậy \(f\left( x \right)\) không phải là hàm chẵn.
Câu 8. Chọn C.
Khi tịnh tiến đồ thị hàm số y = 2x – 3 sang phải 2 đơn vị, rồi xuống dưới 1 đơn vị thì được đồ thị hàm số \(y = 2\left( {x - 2} \right) - 3 - 1 = 2x - 8\) .
Câu 9. Chọn A
Ta có \(y + x\sqrt 2 = 2 \Leftrightarrow y = - x\sqrt 2 + 2\)
Suy ra đường thẳng này song song với đường thẳng \(y = - x\sqrt 2 \) .
Câu 10. Chọn D
Chú ý đồ thị hàm số nằm phía dưới trục hoành nên hàm số có giá trị không dương.
Loigiaihay.com












Danh sách bình luận