Đề khảo sát chất lượng đầu năm Toán 12 - Đề số 2
Đề bài
Với giá trị nào của \(m\) dưới đây thì phương trình \(\sin x = m\) có nghiệm?
-
A.
\(m = - 3\)
-
B.
\(m = - 2\)
-
C.
\(m = 0\)
-
D.
\(m = 3\)
Cho dãy số $\left( {{u_n}} \right)$, biết ${u_n} = \dfrac{{ - n}}{{n + 1}}.$ Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?
-
A.
$ - \dfrac{1}{2}; - \dfrac{2}{3}; - \dfrac{3}{4}; - \dfrac{4}{5}; - \dfrac{5}{6}.$
-
B.
$ - \dfrac{2}{3}; - \dfrac{3}{4}; - \dfrac{4}{5}; - \dfrac{5}{6}; - \dfrac{6}{7}.$
-
C.
$\dfrac{1}{2};\dfrac{2}{3};\dfrac{3}{4};\dfrac{4}{5};\dfrac{5}{6}.$
-
D.
$0; - \dfrac{1}{2}; - \dfrac{2}{3}; - \dfrac{3}{4}; - \dfrac{4}{5}$
Tính $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right)$ bằng?
-
A.
$5$
-
B.
$7$
-
C.
$9$
-
D.
$6$
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:
-
A.
Năm mặt
-
B.
Hai mặt
-
C.
Ba mặt
-
D.
Bốn mặt
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
-
A.
$f\left( x \right) \geqslant - 2,\forall x \in \left[ {1;3} \right]$
-
B.
$f\left( 1 \right) = f\left( 3 \right) = - 2$
-
C.
$f\left( x \right) < - 2,\forall x \in \left[ {1;3} \right]$
-
D.
$f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$
Cho cấp số cộng $6;x; - 2;y$. Khẳng định nào sau đây đúng ?
-
A.
$x = 2,y = 5$
-
B.
$x = 4,y = 6$
-
C.
$x = 2,y = - 6$
-
D.
$x = 4,y = - 6$.
Muốn đi từ A đến B thì bắt buộc phải đi qua C. Có 3 con đường đi từ A tới C và 2 con đường từ C đến B. Số con đường đi từ A đến B là:
-
A.
\(6\)
-
B.
\(5\)
-
C.
\(1\)
-
D.
\(7\)
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
-
A.
\(y = \sin x - 3x\)
-
B.
\(y = \cos x + 2x\)
-
C.
\(y = {x^3}\)
-
D.
\(y = {x^5}\)
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
-
A.
$\mathop{\max}\limits_{x\in\mathbb{R}}f\left(x\right)=3$
-
B.
Hàm số đồng biến trên khoảng$\left( { - \infty ;3} \right)$
-
C.
Giá trị cực tiểu của hàm số bằng 2
-
D.
$\mathop {\min }\limits_{x \in \left[ {0;4} \right]} f\left( x \right) = - 1$
Cho các hình sau: hình chóp tam giác đều, hình hộp đứng, hình lăng trụ tam giác đều, hình chóp tứ giác có đáy là hình thoi, hình hộp có đáy là hình thoi. Số hình có mặt phẳng đối xứng là:
-
A.
\(5\)
-
B.
\(4\)
-
C.
\(3\)
-
D.
\(2\)
Ba số dương lập thành cấp số nhân, tích của số hạng thứ nhất và số hạng thứ ba bằng $36$. Một cấp số cộng có $n$ số hạng, công sai $d = 4$, tổng các số hạng bằng $510$. Biết số hạng đầu của cấp số cộng bằng số hạng thứ 2 của cấp số nhân. Khi đó $n$ bằng:
-
A.
$12$
-
B.
$13$
-
C.
$14$
-
D.
$15$
Cho hàm số $y = {x^4} - 2m{x^2} + {m^2} + m.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác có một góc ${120^o}$ là:
-
A.
$m = \dfrac{1}{{\sqrt[3]{3}}}$
-
B.
$m = 0;\,m = \dfrac{1}{{\sqrt[3]{3}}}$
-
C.
$m = \dfrac{1}{{\sqrt[3]{2}}}$
-
D.
$m = 1$
Hình vẽ sau đây là hình trải phẳng của khối đa diện đều nào?
-
A.
không có khối đa diện đều nào
-
B.
hình lập phương
-
C.
mười hai mặt đều
-
D.
hai mươi mặt đều
Phương trình \(\tan \dfrac{x}{2} = \tan x\) có nghiệm:
-
A.
\(k2\pi \left( {k \in Z} \right)\)
-
B.
\(k\pi \left( {k \in Z} \right)\)
-
C.
\(\pi + k2\pi \left( {k \in Z} \right)\)
-
D.
Cả 3 đáp án đúng
Cho \(C_{x + 1}^y:C_x^{y + 1}:C_x^{y - 1} = 6:5:2\). Khi đó tổng $x + y$ bằng:
-
A.
$3$
-
B.
$ - 8$
-
C.
$11$
-
D.
$ - 3$
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) sao cho \(f\left( { - 1} \right) = 2\), \(f\left( 4 \right) = 7\). Có thể nói gì về số nghiệm của phương trình \(f\left( x \right) = 5\) trên đoạn \([ - 1;4]\):
-
A.
Vô nghiệm.
-
B.
Có ít nhất một nghiệm.
-
C.
Có đúng một nghiệm.
-
D.
Có đúng hai nghiệm.
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x}$
-
A.
$\dfrac{{23}}{2}$.
-
B.
$24$.
-
C.
$\dfrac{3}{2}$.
-
D.
$3$.
Viết phương trình tiếp tuyến $d$ của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) tại điểm có hoành độ \({x_0}\) thỏa mãn \(f''\left( {{x_0}} \right) = 0?\)
-
A.
\(3x + y - 3 = 0\)
-
B.
\(3x - y - 3 = 0\)
-
C.
\( - 3x + y - 3 = 0\)
-
D.
\(3x + y + 3 = 0\)
Trong mặt phẳng tọa độ $Oxy$. Cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt có phương trình \(x - 2y + 1 = 0\) và \(x - 2y + 4 = 0\), điểm \(I\left( {2;1} \right)\). Phép vị tự tâm $I$ tỉ số $k$ biến đường thẳng \({\Delta _1}\) thành \({\Delta _2}\) khi đó giá trị của $k$ là :
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Cho mặt phẳng $\left( {ABC} \right)$ và hai điểm $D,E$ nằm ngoài mặt phẳng $\left( {ABC} \right)$ . Một đường thẳng $a$ nằm trong mặt phẳng $\left( {ABC} \right)$ . Khẳng định nào sau đây đúng?
-
A.
Nếu $DE$ song song với $a$ thì tồn tại giao điểm $M$ của $DE$ và mặt phẳng $\left( {ABC} \right)$ nằm ngoài đường thẳng $a$
-
B.
Nếu $DE$ cắt $a$ tại $M$ thì $M$ là giao điểm của $DE$ và mặt phẳng $\left( {ABC} \right)$
-
C.
Nếu $DE$ cắt $a$ tại $M$ thì tồn tại giao điểm $M$ của $DE$ và mặt phẳng $\left( {ABC} \right)$ nằm ngoài đường thẳng $a$
-
D.
Nếu $DE$ song song với $a$ thì tồn tại giao điểm $M$ của $DE$ và mặt phẳng $\left( {ABC} \right)$ nằm trên đường thẳng $a$
Cho tứ diện $ABCD.$ Gọi $M, N$ lần lượt là trung điểm của các cạnh $AD $ và $ BC, G$ là trọng tâm tam giác $BCD.$ Khi đó giao điểm của đường thẳng $MG$ và $mp(ABC)$ là:
-
A.
Điểm $C$
-
B.
Giao điểm của đường thẳng $MG$ và đường thẳng $AN$
-
C.
Điểm $N$
-
D.
Giao điểm của đường thẳng $MG$ và đường thẳng $ BC$
Cho tứ diện $ABCD,$ gọi $G$ là trọng tâm tam giác $ACD,$ $M$ thuộc đoạn thẳng $BC$ sao cho $CM = 2MB.$ Chọn mệnh đề đúng trong các mệnh đề sau?
-
A.
$MG // (ABC)$
-
B.
$MG // (ABD)$
-
C.
$MG // CD$
-
D.
$MG // BD$
Cho tứ diện $ABCD$ có \(AB = a,CD = b,AB \bot CD\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$ . Mặt phẳng \(\left( \alpha \right)\) qua $M$ nằm trên đoạn $IJ$ và song song với $AB$ và $CD$. Giao tuyến của mặt phẳng \(\left( \alpha \right)\) và hình chóp có diện tích bằng bao nhiêu, biết $IJ = 3IM$
-
A.
\(\dfrac{{2ab}}{3}\)
-
B.
\(\dfrac{{2ab}}{9}\)
-
C.
\(\dfrac{{ab}}{3}\)
-
D.
\(\dfrac{{ab}}{9}\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
-
A.
$(NOM)$ cắt $(OPM)$
-
B.
$(MON) // (SBC)$
-
C.
\(\left( {PON} \right) \cap \left( {MNP} \right) = NP\)
-
D.
\(\left( {MNP} \right)//\left( {SBD} \right)\)
Cho hai hình vuông $ABCD,ABEF$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo $AC$ và $BF$ ta lấy các điểm $M, N$ sao cho $AM = BN.$ Mặt phẳng $(P)$ chứa $MN$ và song song với $AB$ cắt $AD$ và $AF$ lần lượt tại $M’, N’.$ Khẳng định nào sau đây là đúng?
-
A.
$AC, BF$ cắt nhau
-
B.
Tứ giác $MNM’N’$ là hình bình hành
-
C.
$MN$ song song với $(DEF)$
-
D.
$MN$ cắt $(DEF)$
Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình thoi $\widehat {BAD} = {60^0}$ và $A'A = A'B = A'D$. Gọi $O = AC \cap BD$. Hình chiếu của $A'$ trên $\left( {ABCD} \right)$ là :
-
A.
trung điểm của $AO.$
-
B.
trọng tâm $\Delta ABD.$
-
C.
giao của hai đoạn $AC$ và $BD.$
-
D.
trọng tâm$\Delta BCD.$
Cho tam giác \(ABC\) vuông cân tại \(A\) và \(BC = a.\) Trên đường thẳng qua \(A\) vuông góc với \(\left( {ABC} \right)\) lấy điểm \(S\) sao cho $SA = \dfrac{{a\sqrt 6 }}{2}$. Tính số đo góc giữa đường thẳng \(SA\) và \(\left( {ABC} \right)\)
-
A.
\(30^\circ \).
-
B.
\(45^\circ \).
-
C.
\(60^\circ \).
-
D.
\(90^\circ \).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Đường thẳng $SO$ vuông góc với mặt phẳng đáy $\left( {ABCD} \right)$ và $SO = \dfrac{{a\sqrt 3 }}{2}$. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$.
-
A.
${30^0}.$
-
B.
${45^0}.$
-
C.
${60^0}.$
-
D.
${90^0}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $I$, cạnh $a$, góc $\widehat {BAD} = {60^0}$, $SA = SB = SD = \dfrac{{a\sqrt 3 }}{2}$. Gọi \(\varphi \) là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right).$ Mệnh đề nào sau đây đúng?
-
A.
$\tan \varphi = \sqrt 5 .$
-
B.
$\tan \varphi = \dfrac{{\sqrt 5 }}{5}.$
-
C.
$\tan \varphi = \dfrac{{\sqrt 3 }}{2}.$
-
D.
$\varphi = {45^0}.$
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.
-
A.
$1.$
-
B.
$\sqrt 2 .$
-
C.
$2.$
-
D.
$4.$
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
-
A.
\(d = a\sqrt 3 .\)
-
B.
\(d = 5a\sqrt 3 .\)
-
C.
\(d = \dfrac{{5a}}{2}.\)
-
D.
\(d = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm:
-
A.
$x = 2$
-
B.
$x = 0$
-
C.
$x = 3$
-
D.
$x = - 1$
Tiếp tuyến kẻ từ điểm $\left( {2;3} \right)$ tới đồ thị hàm số $y = \dfrac{{3x + 4}}{{x - 1}}$ là
-
A.
$y = - 28x + 59$ ; $y = x + 1$.
-
B.
$y = -24x + 51$; $y = x + 1$.
-
C.
$y = - 28x + 59$.
-
D.
$y = - 28x + 59$; $y = - 24x + 51$.
Cho hàm số \(f\left( x \right) = - 4{x^3} + 4x - 1.\) Mệnh đề nào sau đây là sai?
-
A.
Hàm số đã cho liên tục trên \(\mathbb{R}.\)
-
B.
Phương trình \(f\left( x \right) = 0\) không có nghiệm trên khoảng \(\left( { - \infty ;1} \right).\)
-
C.
Phương trình \(f\left( x \right) = 0\) có nghiệm trên khoảng \(\left( { - 2;0} \right).\)
-
D.
Phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm trên khoảng \(\left( { - 3;\dfrac{1}{2}} \right).\)
Cho tứ diện \(ABCD\) có \(AB \bot CD\) và \(AC \bot BD\). Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(mp(BCD)\). Chọn khẳng định đúng :
-
A.
\(H\) là trọng tâm tam giác \(BCD\).
-
B.
\(CD \bot (ACH)\).
-
C.
\(AD \bot BC\).
-
D.
Các khẳng định trên đều đúng.
Cho hình chóp \(S.ABC\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tâm \(O\). Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(\varphi \) là góc giữa \(SO\) và mặt phẳng \(\left( {ABCD} \right)\). Mệnh đề nào sau đây đúng?
-
A.
\(\tan \varphi = 2\sqrt 2 .\)
-
B.
\(\varphi = {60^0}.\)
-
C.
\(\tan \varphi = 2.\).
-
D.
\(\varphi = {45^0}.\)
Đồ thị hàm số \(y = \tan x\) nhận đường thẳng nào sau đây là tiệm cận?
-
A.
\(y = \dfrac{\pi }{3} + k\pi \left( {k \in Z} \right)\)
-
B.
\(x = k\pi \left( {k \in Z} \right)\)
-
C.
\(x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
-
D.
\(y = \dfrac{{k\pi }}{2}\left( {k \in Z} \right)\)
Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau
\(y = 3{\left( {3\sin x + 4\cos x} \right)^2} + 4\left( {3\sin x + 4\cos x} \right) + 1\)
-
A.
\(\min y = \dfrac{1}{3};\max y = 96\)
-
B.
\(\min y = \dfrac{1}{3};\max y = 6\)
-
C.
\(\min y = - \dfrac{1}{3};\max y = 96\)
-
D.
\(\min y = 2;\max y = 6\)
Trên giá sách có $6$ quyển Văn khác nhau, $5$ quyển sách Toán khác nhau và $9$ quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?
-
A.
$54$
-
B.
$405$
-
C.
$30$
-
D.
$129$
Để phương trình \({\sin ^2}x + 2\left( {m + 1} \right)\sin x - 3m\left( {m - 2} \right) = 0\) có nghiệm, các giá trị của tham số m là:
-
A.
\(\left[ \begin{array}{l} - \dfrac{1}{2} \le m \le \dfrac{1}{2}\\1 \le m \le 2\end{array} \right.\)
-
B.
\(\left[ \begin{array}{l} - \dfrac{1}{3} \le m \le \dfrac{1}{3}\\1 \le m \le 3\end{array} \right.\)
-
C.
\(\left[ \begin{array}{l} - 2 \le m \le - 1\\0 \le m \le 1\end{array} \right.\)
-
D.
\(\left[ \begin{array}{l} - 1 \le m \le 1\\3 \le m \le 4\end{array} \right.\)
Nghiệm của phương trình \(\cos 7x\cos 5x - \sqrt 3 \sin 2x = 1 - \sin 7x\sin 5x\) là:
-
A.
$\left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
-
B.
$\left[ \begin{array}{l}x = k\pi \\x = - \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
-
C.
$x = k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)$
-
D.
$\left[ \begin{array}{l}x = k2\pi \\x = - \dfrac{\pi }{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
Giá trị của $n$ thỏa mãn $3A_n^2 - A_{2n}^2 + 42 = 0$ là
-
A.
$9$.
-
B.
$8$.
-
C.
$6$.
-
D.
$10$.
Một con xúc sắc cân đối và đồng chất được gieo ba lần. Gọi $P$ là xác suất để tổng số chấm xuất hiện ở hai lần gieo đầu bằng số chấm xuất hiện ở lần gieo thứ ba. Khi đó $P$ bằng:
-
A.
$\dfrac{{10}}{{216}}$.
-
B.
$\dfrac{{15}}{{216}}$.
-
C.
$\dfrac{{16}}{{216}}$.
-
D.
$\dfrac{{12}}{{216}}$.
Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
-
A.
$5.2500.000$ đồng
-
B.
$10.125.000$ đồng
-
C.
$4.000.000$ đồng
-
D.
$4.245.000$ đồng
Trong các dãy số $\left( {{u_n}} \right)$ cho bởi số hạng tổng quát ${u_n}$ sau, dãy số nào là một cấp số nhân?
-
A.
\({u_n} = 7 - 3n.\)
-
B.
\({u_n} = 7 - {3^n}.\)
-
C.
\({u_n} = \dfrac{7}{{3n}}.\)
-
D.
\({u_n} = {7.3^n}.\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 - 4t\\y = 1 + t\end{array} \right..\)Ảnh của đường thẳng \(\Delta \) qua phép đối xứng tâm \(I\left( { - 2;2} \right)\) có phương trình là:
-
A.
\(x + 4y - 5 = 0.\)
-
B.
\(x + 4y - 6 = 0.\)
-
C.
$4x - y + 1 = 0.$
-
D.
\(4x - y - 1 = 0.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).
-
A.
\(13\)
-
B.
$11$
-
C.
$10$
-
D.
$12$
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
-
A.
\(1\).
-
B.
\(\dfrac{1}{3}\).
-
C.
\(\dfrac{2}{3}\).
-
D.
\(\dfrac{1}{2}\).
Cho tứ diện \(ABCD\) có \(AB = CD = 4,BC = AD = 5,AC = BD = 6\). \(M\) là điểm thay đổi trong tâm giác \(ABC\). Các đường thẳng qua \(M\) song song với \(AD,BD,CD\) tương ứng cắt mặt phẳng \(\left( {BCD} \right),\left( {ACD} \right),\left( {ABD} \right)\) tại \(A',B',C'\). Giá trị lớn nhất của \(MA'.MB'.MC'\) là
-
A.
\(\dfrac{{40}}{9}\)
-
B.
\(\dfrac{{24}}{9}\)
-
C.
\(\dfrac{{30}}{9}\)
-
D.
\(\dfrac{{20}}{9}\)
Cho hàm số \(f\left( x \right)\) có bảng xét dấu có đạo hàm như hình bên dưới
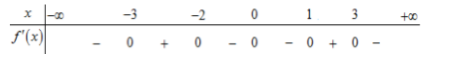
Hàm số \(y = f\left( {1 - 2x} \right)\) đồng biến trên khoảng
-
A.
\(\left( {0;\dfrac{3}{2}} \right)\)
-
B.
\(\left( { - \dfrac{1}{2};1} \right)\)
-
C.
\(\left( { - 2; - \dfrac{1}{2}} \right)\)
-
D.
\(\left( {\dfrac{3}{2};3} \right)\)
Lời giải và đáp án
Với giá trị nào của \(m\) dưới đây thì phương trình \(\sin x = m\) có nghiệm?
-
A.
\(m = - 3\)
-
B.
\(m = - 2\)
-
C.
\(m = 0\)
-
D.
\(m = 3\)
Đáp án : C
Phương trình \(\sin x = m\) có nghiệm nếu \(\left| m \right| \le 1\) và vô nghiệm nếu \(\left| m \right| > 1\)
Đáp án A: $|m|=|-3|=3>1$=> Loại
Đáp án B: $|m|=|-2|=2>1$=> Loại
Đáp án C: $|m|=|0|=0\le 1$ => Nhận
Đáp án D: $|m|=|3|=3>1$=> Loại
Một số em có thể sẽ chọn nhầm đáp án D vì nghĩ \(m > 0\) thì phương trình có nghiệm là sai.
Cho dãy số $\left( {{u_n}} \right)$, biết ${u_n} = \dfrac{{ - n}}{{n + 1}}.$ Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?
-
A.
$ - \dfrac{1}{2}; - \dfrac{2}{3}; - \dfrac{3}{4}; - \dfrac{4}{5}; - \dfrac{5}{6}.$
-
B.
$ - \dfrac{2}{3}; - \dfrac{3}{4}; - \dfrac{4}{5}; - \dfrac{5}{6}; - \dfrac{6}{7}.$
-
C.
$\dfrac{1}{2};\dfrac{2}{3};\dfrac{3}{4};\dfrac{4}{5};\dfrac{5}{6}.$
-
D.
$0; - \dfrac{1}{2}; - \dfrac{2}{3}; - \dfrac{3}{4}; - \dfrac{4}{5}$
Đáp án : A
Thay lần lượt các giá trị \(n = 1,2,3,4,5\) vào công thức số hạng tổng quát của dãy số.
Ta có \({u_1} = - \dfrac{1}{2};{u_2} = - \dfrac{2}{3};{u_3} = - \dfrac{3}{4};\) \({u_4} = - \dfrac{4}{5};{u_5} = - \dfrac{5}{6}.\)
Một số em có thể thay nhầm giá trị đầu tiên \(n = 0\) và chọn nhầm đáp án D là sai. Cần chú ý dãy số là hàm số xác định trên tập \({N^*}\).
Tính $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right)$ bằng?
-
A.
$5$
-
B.
$7$
-
C.
$9$
-
D.
$6$
Đáp án : C
Hàm số \(y = f\left( x \right)\) xác định tại \(x = {x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} = f\left( {{x_0}} \right)\)
$\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right) = {( - 1)^2} - ( - 1) + 7 = 9.$
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:
-
A.
Năm mặt
-
B.
Hai mặt
-
C.
Ba mặt
-
D.
Bốn mặt
Đáp án : C
Sử dụng phương pháp chọn điểm rơi, lấy ví dụ cho hình tứ diện và suy ra đáp án.
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt (ví dụ các đỉnh của hình tứ diện)
Không tồn tại 1 đỉnh nào đó của đa diện nào đó là đỉnh chung của ít hơn 3 mặt
Một số em lấy ví dụ tứ diện nhưng tính nhầm mối đỉnh là đỉnh chung của \(4\) mặt và chọn D là sai.
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
-
A.
$f\left( x \right) \geqslant - 2,\forall x \in \left[ {1;3} \right]$
-
B.
$f\left( 1 \right) = f\left( 3 \right) = - 2$
-
C.
$f\left( x \right) < - 2,\forall x \in \left[ {1;3} \right]$
-
D.
$f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$
Đáp án : D
Nếu $M = - 2$ là GTLN của hàm số $y = f\left( x \right)$ trên $\left[ {1;3} \right]$ thì $f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$.
Cho cấp số cộng $6;x; - 2;y$. Khẳng định nào sau đây đúng ?
-
A.
$x = 2,y = 5$
-
B.
$x = 4,y = 6$
-
C.
$x = 2,y = - 6$
-
D.
$x = 4,y = - 6$.
Đáp án : C
Sử dụng tính chất của CSC \({u_{n - 1}} + {u_{n + 1}} = 2{u_n}\)
Ta có \(\left\{ \begin{array}{l}6 - 2 = 2x\\x + y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 6\end{array} \right.\)
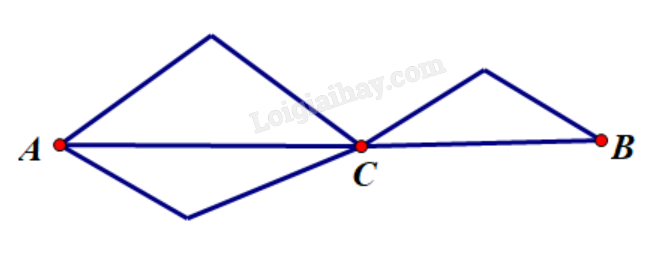
Muốn đi từ A đến B thì bắt buộc phải đi qua C. Có 3 con đường đi từ A tới C và 2 con đường từ C đến B. Số con đường đi từ A đến B là:

-
A.
\(6\)
-
B.
\(5\)
-
C.
\(1\)
-
D.
\(7\)
Đáp án : A
Có \(2\) công đoạn đi từ \(A\) đến \(B\) là: đi từ \(A\) đến \(C\) và đi từ \(C\) đến \(B\).
- Có \(3\) con đường từ \(A\) đến \(C\).
- Có \(2\) con đường từ \(C\) đến \(B\).
Vậy có \(3.2 = 6\) con đường đi từ \(A\) đến \(B\).
Một số em có thể sẽ chọn nhầm đáp án D vì nghĩ rằng còn có thêm một cách đi thẳng từ \(A\) đến \(B\) mà không cần qua \(C\) là sai vì đề bài cho bắt buộc phải qua \(C\).
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
-
A.
\(y = \sin x - 3x\)
-
B.
\(y = \cos x + 2x\)
-
C.
\(y = {x^3}\)
-
D.
\(y = {x^5}\)
Đáp án : A
+) Xét các hàm số theo từng đáp án.
+) Hàm số nào có $y' \ge 0$ với mọi $x \in R$ thì hàm số đó đồng biến trên R.
+) Xét đáp án A:$y = \sin x - 3x$ có: $y' = \cos x - 3.$
Với $\forall {\mkern 1mu} {\mkern 1mu} x \in R$ ta có: $ - 1 \le \cos x \le 1 \Rightarrow y' = {\rm{cosx\;}} - 3 < 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x{\mkern 1mu} {\mkern 1mu} \in R \Rightarrow $ hàm số nghịch biến trên $R.$
Vậy hàm số ở đáp án A không đồng biến trên $R$.
+) Xét đáp án B: $y = \cos x + 2x$ có: $y' = {\rm{\;}} - \sin x + 2.$
Với $\forall {\mkern 1mu} {\mkern 1mu} x \in R$ ta có: $ - 1 \le \sin x \le 1 \Rightarrow y' = {\rm{\;}} - \sin x + 2 > 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x{\mkern 1mu} {\mkern 1mu} \in R$
Vậy hàm số đồng biến trên $\mathbb{R}.$
+) Xét đáp án C: $y'=3x^2\ge 0, \forall x$ nên hàm số đồng biến trên $R$.
+) Xét đáp án D: $y'=5x^4\ge 0, \forall x$ nên hàm số đồng biến trên $R$.
Vậy chỉ có hàm số ở đáp án A không đồng biến trên $R$.
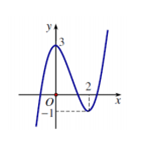
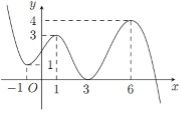
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?

-
A.
$\mathop{\max}\limits_{x\in\mathbb{R}}f\left(x\right)=3$
-
B.
Hàm số đồng biến trên khoảng$\left( { - \infty ;3} \right)$
-
C.
Giá trị cực tiểu của hàm số bằng 2
-
D.
$\mathop {\min }\limits_{x \in \left[ {0;4} \right]} f\left( x \right) = - 1$
Đáp án : D
Quan sát đồ thị hàm số và rút ra các nhận xét về cực đại, cực tiểu, GTLN, GTNN, khoảng đồng biến, nghịch biến.
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Học sinh thường nhầm lẫn cách tìm GTLN, GTNN của hàm số với giá trị cực đại, giá trị cực tiểu của hàm số. nên có thể chọn A là sai.
Cho các hình sau: hình chóp tam giác đều, hình hộp đứng, hình lăng trụ tam giác đều, hình chóp tứ giác có đáy là hình thoi, hình hộp có đáy là hình thoi. Số hình có mặt phẳng đối xứng là:
-
A.
\(5\)
-
B.
\(4\)
-
C.
\(3\)
-
D.
\(2\)
Đáp án : C
Các hình có mặt phẳng đối xứng là:
+ Hình chóp tam giác đều có \(3\) mặt phẳng đối xứng.
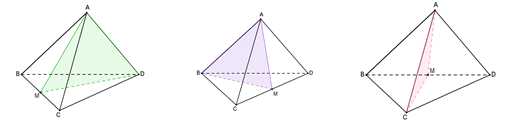
+ Hình hộp đứng có \(1\) mặt phẳng đối xứng.
+ Hình lăng trụ tam giác đều có \(4\) mặt phẳng đối xứng.
+ Hình hộp có đáy là hình thoi không có mặt phẳng đối xứng.
+ Hình chóp tứ giác có đáy là hình thoi không có mặt phẳng đối xứng.
Vậy có \(3\) hình có mặt phẳng đối xứng.
Một số em nhầm hình chóp tứ giác có đáy là hình thoi cũng có mặt phẳng đối xứng và chọn đáp án B là sai. Một số khác thì nhầm hình hộp có đáy là hình thoi cũng có mặt phẳng đối xứng và chọn đáp án A hoặc B là sai.
Ba số dương lập thành cấp số nhân, tích của số hạng thứ nhất và số hạng thứ ba bằng $36$. Một cấp số cộng có $n$ số hạng, công sai $d = 4$, tổng các số hạng bằng $510$. Biết số hạng đầu của cấp số cộng bằng số hạng thứ 2 của cấp số nhân. Khi đó $n$ bằng:
-
A.
$12$
-
B.
$13$
-
C.
$14$
-
D.
$15$
Đáp án : D
- Sử dụng tính chất của cấp số nhân để tính số hạng thứ hai của cấp số nhân và cũng là số hạng đầu tiên của cấp số cộng.
- Sử dụng công thức tổng \(n\) số hạng đầu tiên của cấp số cộng để tìm \(n\).
Với cấp số nhân \(a,b,c > 0 \Rightarrow {b^2} = ac = 36 \Rightarrow b = 6 > 0\)
Do đó, theo giả thiết cấp số cộng ta có
\({u_1} = 6;d = 4;{S_n} = 510\)
\(\begin{array}{l}{S_n} = \dfrac{n}{2}\left( {2{u_1} + (n - 1)d} \right) \Leftrightarrow 510 = \dfrac{n}{2}\left( {12 + 4(n - 1)} \right)\\ \Leftrightarrow {n^2} + 2n - 255 = 0\\ \Rightarrow n = 15\end{array}\)
(do n nguyên dương)
Cho hàm số $y = {x^4} - 2m{x^2} + {m^2} + m.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác có một góc ${120^o}$ là:
-
A.
$m = \dfrac{1}{{\sqrt[3]{3}}}$
-
B.
$m = 0;\,m = \dfrac{1}{{\sqrt[3]{3}}}$
-
C.
$m = \dfrac{1}{{\sqrt[3]{2}}}$
-
D.
$m = 1$
Đáp án : A
- Bước 1: Tính $y'$.
- Bước 2: Ba điểm cực trị $A,B,C$ trong đó $A\left( {0;c} \right)$ tạo thành tam giác cân có góc ở đỉnh bằng $\alpha $ cho trước$ \Leftrightarrow \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} }\right|.\left| {\overrightarrow {AC} } \right|}} = \cos \alpha $
- Bước 3: Kết luận.
\(\begin{array}{l}y' = 4{x^3} - 4mx\\y' = 0 \Leftrightarrow 4{x^3} - 4mx = 0 \Leftrightarrow 4x\left( {{x^2} - m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt m \end{array} \right.\end{array}\)
Điều kiện để hàm số có $3$ cực trị: \(m > 0\)
\(\begin{array}{l}x = 0 \Rightarrow A\left( {0;\,{m^2} + m} \right)\\x = - \sqrt m \Rightarrow y = {\left( { - \sqrt m } \right)^4} - 2m{\left( { - \sqrt m } \right)^2} + {m^2} + m \\= {m^2} - 2{m^2} + {m^2} + m = m \Rightarrow B\left( { - \sqrt m ;\,m} \right)\\x = \sqrt m \Rightarrow C\left( {\sqrt m ;\,m} \right)\end{array}\)
$\begin{array}{l}
\overrightarrow {AB} = \left( { - \sqrt m ; - {m^2}} \right),\overrightarrow {AC} = \left( {\sqrt m ; - {m^2}} \right)\\
\widehat {BAC} = {120^0}\\
\Leftrightarrow \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \cos {120^0}\\
\Leftrightarrow \dfrac{{ - m + {m^4}}}{{\sqrt {m + {m^4}} .\sqrt {m + {m^4}} }} = - \dfrac{1}{2}\\
\Leftrightarrow 2\left( {{m^4} - m} \right) = - \left( {m + {m^4}} \right)\\
\Leftrightarrow 3{m^4} - m = 0\\
\Leftrightarrow m\left( {3{m^3} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
m = 0\left( {loai} \right)\\
m = \dfrac{1}{{\sqrt[3]{3}}}
\end{array} \right.
\end{array}$
Cách tự luận cũng có thể làm như sau:
\(\begin{array}{l}\widehat {BAC} = {120^o} \Rightarrow \widehat {HAC} = {60^o}\\ \Rightarrow HC = AH.\tan {60^o}\\ \Leftrightarrow \left| {{x_C}} \right| = \left| {{y_A} - {y_C}} \right|.\sqrt 3 \\ \Leftrightarrow \left| { - \sqrt m } \right| = \left| {{m^2}} \right|.\sqrt 3 \\ \Leftrightarrow m = {m^4}.3\\ \Leftrightarrow 3{m^4} - m = 0\\ \Leftrightarrow m\left( {3{m^3} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\{m^3} = \dfrac{1}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = \dfrac{1}{{\sqrt[3]{3}}}\end{array} \right.\end{array}\)
Kết hợp với điều kiện \(m > 0 \Rightarrow m = \dfrac{1}{{\sqrt[3]{3}}}\)
Ngoài ra, cách trắc nghiệm ta làm như sau:
Ta có thể sử dụng công thức giải nhanh: Đồ thị hàm số $y = a{x^4} + b{x^2} + c(a \ne 0)$ tạo thành tam giác có góc cân ở đỉnh bằng $\alpha $ cho trước: $\cos \alpha = \dfrac{{{b^3} + 8a}}{{{b^3} - 8a}}$
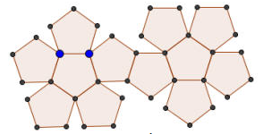
Hình vẽ sau đây là hình trải phẳng của khối đa diện đều nào?

-
A.
không có khối đa diện đều nào
-
B.
hình lập phương
-
C.
mười hai mặt đều
-
D.
hai mươi mặt đều
Đáp án : C
Quan sát hình vẽ ta thấy nó có \(12\) mặt và mỗi mặt là một ngũ giác đều.
Vậy hình vẽ trên là hình trải phẳng của khối mười hai mặt đều.
Phương trình \(\tan \dfrac{x}{2} = \tan x\) có nghiệm:
-
A.
\(k2\pi \left( {k \in Z} \right)\)
-
B.
\(k\pi \left( {k \in Z} \right)\)
-
C.
\(\pi + k2\pi \left( {k \in Z} \right)\)
-
D.
Cả 3 đáp án đúng
Đáp án : A
Bước 1: Tìm điều kiện xác định
Sử dụng công thức $\tan x =\dfrac{\sin x}{\cos x}$ và \(\tan \dfrac{x}{2} = \dfrac{{\sin \dfrac{x}{2}}}{{\cos \dfrac{x}{2}}}\)
$\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi$
Bước 2: Giải phương trình lượng giác cơ bản: \(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in Z} \right)\) và kết hợp với điều kiện xác định để loại nghiệm.
Bước 1:
Điều kiện:\(\left\{ \begin{array}{l}\cos x \ne 0\\\cos \dfrac{x}{2} \ne 0\end{array} \right. \) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi \\\dfrac{x}{2} \ne \dfrac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi \\x \ne \pi + k2\pi \end{array} \right.\)
Bước 2:
Ta có: \(\tan \dfrac{x}{2} = \tan x \Leftrightarrow \dfrac{x}{2} = x + k\pi \) \(\Leftrightarrow - \dfrac{x}{2} = k\pi \Leftrightarrow - x = 2k\pi \) \(\Leftrightarrow x = - k2\pi \left( {k \in Z} \right)\) (*)
Đặt \(k = - l\) nên:
(*)\(\Leftrightarrow x = l2\pi \left( {l \in Z} \right)\) (TMĐK)
Các em có thể nhận xét nhanh, vì điều kiện là \(x \ne \pi + k2\pi \) nên có thể loại này các đáp án B và C, D nên chỉ còn đáp án A là đúng.
Cho \(C_{x + 1}^y:C_x^{y + 1}:C_x^{y - 1} = 6:5:2\). Khi đó tổng $x + y$ bằng:
-
A.
$3$
-
B.
$ - 8$
-
C.
$11$
-
D.
$ - 3$
Đáp án : C
Áp dụng các công thức chỉnh hợp và tổ hợp: \(A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}}\,;\,C_n^k = \dfrac{{n!}}{{k!\left( {n - k} \right)!}}\)
Và áp dụng công thức của tỉ lệ thức: $a:b:c = x:y:z \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{b} = \dfrac{x}{y}\\\dfrac{a}{c} = \dfrac{x}{z}\\\dfrac{b}{c} = \dfrac{y}{z}\end{array} \right.$
ĐK: \(\left\{ \begin{array}{l}x + 1 \ge y \ge 0\\x \ge y + 1 \ge 0\\x \ge y - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y \ge 1\\x \ge y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y \ge 1\\x \ge 2\end{array} \right.\,\,\left( {x,y \in N} \right)\)
\(\begin{array}{l}C_{x + 1}^y:C_x^{y + 1}:C_x^{y - 1} = 6:5:2 \Rightarrow \left\{ \begin{array}{l}\dfrac{{C_{x + 1}^y}}{{C_x^{y + 1}}} = \dfrac{6}{5}\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\dfrac{{C_{x + 1}^y}}{{C_x^{y - 1}}} = \dfrac{6}{2} = 3\,\,\left( 2 \right)\end{array} \right.\\\left( 1 \right) \Leftrightarrow \dfrac{{\dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}}}{{\dfrac{{x!}}{{\left( {y + 1} \right)!\left( {x - y - 1} \right)!}}}} = \dfrac{6}{5}\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}.\dfrac{{\left( {y + 1} \right)!\left( {x - y - 1} \right)!}}{{x!}} = \dfrac{6}{5}\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)\left( {y + 1} \right)}}{{\left( {x - y} \right)\left( {x - y + 1} \right)}} = \dfrac{6}{5}\,\,\,\left( 3 \right)\\\left( 2 \right) \Leftrightarrow \dfrac{{\dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}}}{{\dfrac{{x!}}{{\left( {y - 1} \right)!\left( {x - y + 1} \right)!}}}} = 3\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}\dfrac{{\left( {y - 1} \right)!\left( {x - y + 1} \right)!}}{{x!}} = 3\\ \Leftrightarrow \dfrac{{x + 1}}{y} = 3 \Rightarrow x = 3y - 1\end{array}\)
Thay vào (3) ta có:
\(\begin{array}{l}\dfrac{{3y\left( {y + 1} \right)}}{{\left( {2y - 1} \right)2y}} = \dfrac{6}{5}\\ \Leftrightarrow \dfrac{{y + 1}}{{4y - 2}} = \dfrac{2}{5} \Leftrightarrow 5y + 5 = 8y - 4\\ \Leftrightarrow 3y = 9 \Leftrightarrow y = 3\,\,\left( {tm} \right) \Rightarrow x = 8\,\,\left( {tm} \right)\\ \Rightarrow x + y = 11\end{array}\)
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) sao cho \(f\left( { - 1} \right) = 2\), \(f\left( 4 \right) = 7\). Có thể nói gì về số nghiệm của phương trình \(f\left( x \right) = 5\) trên đoạn \([ - 1;4]\):
-
A.
Vô nghiệm.
-
B.
Có ít nhất một nghiệm.
-
C.
Có đúng một nghiệm.
-
D.
Có đúng hai nghiệm.
Đáp án : B
Xét hàm \(g\left( x \right) = f\left( x \right) - 5\) trên đoạn \([ - 1;4]\), tìm số nghiệm của \(g\left( x \right)\) trong đoạn đó và kết luận.
Ta có \(f\left( x \right) = 5 \Leftrightarrow f\left( x \right) - 5 = 0\). Đặt \(g\left( x \right) = f\left( x \right) - 5.\) Khi đó
\(\left\{ \begin{array}{l}g\left( { - 1} \right) = f\left( { - 1} \right) - 5 = 2 - 5 = - 3\\g\left( 4 \right) = f\left( 4 \right) - 5 = 7 - 5 = 2\end{array} \right. \Rightarrow g\left( { - 1} \right)g\left( 4 \right) < 0.\)
Vậy phương trình \(g\left( x \right) = 0\) có ít nhất một nghiệm thuộc khoảng \(\left( {1;4} \right)\) hay phương trình \(f\left( x \right) = 5\) có ít nhất một nghiệm thuộc khoảng \(\left( {1;4} \right)\).
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x}$
-
A.
$\dfrac{{23}}{2}$.
-
B.
$24$.
-
C.
$\dfrac{3}{2}$.
-
D.
$3$.
Đáp án : D
- Biến đổi biểu thức, đưa về dạng $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt[n]{{1 + nx}} - 1}}{x}$
- Nhân liên hợp.
Ta có:
$\begin{array}{l}\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1\\ = \sqrt {1 + 2x} - \sqrt {1 + 2x} + \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}} - \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}} + \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1\\ = \left( {\sqrt {1 + 2x} - 1} \right) + \sqrt {1 + 2x} \left( {\sqrt[3]{{1 + 3x}} - 1} \right) + \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\left( {\sqrt[4]{{1 + 4x}} - 1} \right)\end{array}$
$\begin{array}{l} \Rightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {1 + 2x} - 1}}{x}} \right) + \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{\sqrt[3]{{1 + 3x}} - 1}}{x}} \right) + \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{\sqrt[4]{{1 + 4x}} - 1}}{x}} \right)\end{array}$
Tính:
$\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {1 + 2x} - 1}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {\sqrt {1 + 2x} - 1} \right)\left( {\sqrt {1 + 2x} + 1} \right)}}{{x\left( {\sqrt {1 + 2x} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{2x}}{{x\left( {\sqrt {1 + 2x} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \dfrac{2}{{\sqrt {1 + 2x} + 1}} = \dfrac{2}{{1 + 1}} = 1$
$\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{\sqrt[3]{{1 + 3x}} - 1}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{\left( {\sqrt[3]{{1 + 3x}} - 1} \right)\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}{{x.\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}} \right)\\ = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{3x}}{{x.\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{3\sqrt {1 + 2x} }}{{\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}} \right) = \dfrac{{3.1}}{{1 + 1 + 1}} = 1\end{array}$
$\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{\sqrt[4]{{1 + 4x}} - 1}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{\left( {\sqrt[4]{{1 + 4x}} - 1} \right)\left[ {{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1} \right]}}{{x\left[ {{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1} \right]}}} \right)\\ = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{4x}}{{x\left[ {{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1} \right]}}} \right)\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{4\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}}}{{{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1}} = \dfrac{{4.1.1}}{{1 + 1 + 1 + 1}} = 1\end{array}$
Vậy $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x} = 1 + 1 + 1 = 3$
Viết phương trình tiếp tuyến $d$ của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) tại điểm có hoành độ \({x_0}\) thỏa mãn \(f''\left( {{x_0}} \right) = 0?\)
-
A.
\(3x + y - 3 = 0\)
-
B.
\(3x - y - 3 = 0\)
-
C.
\( - 3x + y - 3 = 0\)
-
D.
\(3x + y + 3 = 0\)
Đáp án : A
- Tìm điểm có hoành độ \({x_0}\) thuộc đồ thị hàm số.
- Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {{x_o};{y_0}} \right)\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\)
\(\begin{array}{l}y = f\left( x \right) = {x^3} - 3{x^2} + 2\\f'\left( x \right) = 3{x^2} - 6x,f''\left( x \right) = 6x - 6 = 0 \Leftrightarrow x = 1 \Rightarrow y = 0 \Rightarrow M\left( {1;0} \right)\end{array}\)
\(y'\left( 1 \right) = - 3 \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại \(M\left( {1;0} \right)\) là \(y = - 3\left( {x - 1} \right) + 0 \Leftrightarrow 3x + y - 3 = 0\)
Trong mặt phẳng tọa độ $Oxy$. Cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt có phương trình \(x - 2y + 1 = 0\) và \(x - 2y + 4 = 0\), điểm \(I\left( {2;1} \right)\). Phép vị tự tâm $I$ tỉ số $k$ biến đường thẳng \({\Delta _1}\) thành \({\Delta _2}\) khi đó giá trị của $k$ là :
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : D
Lấy điểm $A$ bất kì thuộc \({\Delta _1}\), tìm ảnh $A'$ của $A$ qua phép vị tự tâm $I$ tỉ số $k$.
Thay tọa độ điểm $A'$ vừa tìm được vào phương trình đường thẳng \({\Delta _2}\).
Lấy \(A\left( { - 1;0} \right) \in {\Delta _1}\), gọi \(A'\left( {x;y} \right)\) là ảnh của $A$ qua phép vị tự tâm $I$ tỉ số $k$ ta có : \(\overrightarrow {IA'} = k\overrightarrow {IA} \)
\(\begin{array}{l} \Rightarrow \left( {x - 2;y - 1} \right) = k\left( { - 3; - 1} \right) \Leftrightarrow \left\{ \begin{array}{l}x - 2 = - 3k\\y - 1 = - k\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = - 3k + 2\\y = - k + 1\end{array} \right. \Rightarrow A'\left( { - 3k + 2; - k + 1} \right)\\{V_{\left( {I;k} \right)}}\left( {{\Delta _1}} \right) = {\Delta _2},\,\,{V_{\left( {I;k} \right)}}\left( A \right) = A' \Rightarrow A' \in {\Delta _2}\end{array}\)
Thay tọa độ điểm $A'$ vào phương trình đường thẳng \({\Delta _2}\) ta có:
\( - 3k + 2 - 2\left( { - k + 1} \right) + 4 = 0 \Leftrightarrow - k + 4 = 0 \Leftrightarrow k = 4\)
Cho mặt phẳng $\left( {ABC} \right)$ và hai điểm $D,E$ nằm ngoài mặt phẳng $\left( {ABC} \right)$ . Một đường thẳng $a$ nằm trong mặt phẳng $\left( {ABC} \right)$ . Khẳng định nào sau đây đúng?
-
A.
Nếu $DE$ song song với $a$ thì tồn tại giao điểm $M$ của $DE$ và mặt phẳng $\left( {ABC} \right)$ nằm ngoài đường thẳng $a$
-
B.
Nếu $DE$ cắt $a$ tại $M$ thì $M$ là giao điểm của $DE$ và mặt phẳng $\left( {ABC} \right)$
-
C.
Nếu $DE$ cắt $a$ tại $M$ thì tồn tại giao điểm $M$ của $DE$ và mặt phẳng $\left( {ABC} \right)$ nằm ngoài đường thẳng $a$
-
D.
Nếu $DE$ song song với $a$ thì tồn tại giao điểm $M$ của $DE$ và mặt phẳng $\left( {ABC} \right)$ nằm trên đường thẳng $a$
Đáp án : B
Tìm giao điểm của $DE$ và mặt phẳng $\left( {ABC} \right)$ :
+ Cách 1: Nếu tồn tại một đường thẳng $a \subset \left( {ABC} \right)$ và $DE$ cắt $a$ tại $M$ thì $M$ chính là giao điểm của $DE$ và mặt phẳng $\left( {ABC} \right)$
+ Cách 2: Tìm mặt phẳng chứa $DE$ cắt $\left( {ABC} \right)$
Khẳng định B là đúng
Cho tứ diện $ABCD.$ Gọi $M, N$ lần lượt là trung điểm của các cạnh $AD $ và $ BC, G$ là trọng tâm tam giác $BCD.$ Khi đó giao điểm của đường thẳng $MG$ và $mp(ABC)$ là:
-
A.
Điểm $C$
-
B.
Giao điểm của đường thẳng $MG$ và đường thẳng $AN$
-
C.
Điểm $N$
-
D.
Giao điểm của đường thẳng $MG$ và đường thẳng $ BC$
Đáp án : B
Đừa về cùng mặt phẳng. Tìm trong mặt phẳng $(SAB)$ một đường thẳng cắt $DY.$ Giao điểm của đường thẳng đó và $SO$ chính là giao điểm của $(SAB)$ và $DY.$
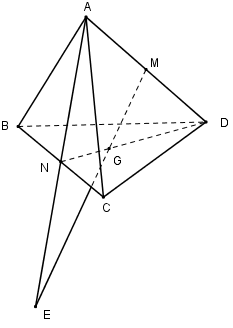
Ta có: \(\dfrac{{DM}}{{DA}} \ne \dfrac{{DG}}{{DN}}\,\,\left( {\dfrac{1}{2} \ne \dfrac{2}{3}} \right) \)
\(\Rightarrow \) $MG$ và $AN$ không song song với nhau.
Trong $(ADN)$ gọi \(E = MG \cap AN.\) Mà \(AN \subset \left( {ABC} \right) \Rightarrow MG \cap \left( {ABC} \right) = E.\)
Cho tứ diện $ABCD,$ gọi $G$ là trọng tâm tam giác $ACD,$ $M$ thuộc đoạn thẳng $BC$ sao cho $CM = 2MB.$ Chọn mệnh đề đúng trong các mệnh đề sau?
-
A.
$MG // (ABC)$
-
B.
$MG // (ABD)$
-
C.
$MG // CD$
-
D.
$MG // BD$
Đáp án : B
- Đưa về cùng một mặt phẳng.
- Sử dụng tính chất trọng tâm của tam giác.
- Áp dụng định lí Ta – let đảo để chứng minh hai đường thẳng song song.
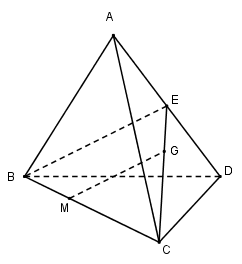
Gọi $E$ là trung điểm của $AD$ ta có \(G \in CE\) và \(\dfrac{{CG}}{{CE}} = \dfrac{2}{3}\)
Vì \(CM = 2MB \Rightarrow \dfrac{{CM}}{{CB}} = \dfrac{2}{3}\)
Xét tam giác $BCE$ có: \(\dfrac{{CG}}{{CE}} = \dfrac{{CM}}{{CB}} = \dfrac{2}{3} \)
\(\Rightarrow \) $MG // BE$ (Định lí Ta – let đảo)
Mà \(BE \subset \left( {ABD} \right)\) \( \Rightarrow \) $MG // (ABD)$
Cho tứ diện $ABCD$ có \(AB = a,CD = b,AB \bot CD\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$ . Mặt phẳng \(\left( \alpha \right)\) qua $M$ nằm trên đoạn $IJ$ và song song với $AB$ và $CD$. Giao tuyến của mặt phẳng \(\left( \alpha \right)\) và hình chóp có diện tích bằng bao nhiêu, biết $IJ = 3IM$
-
A.
\(\dfrac{{2ab}}{3}\)
-
B.
\(\dfrac{{2ab}}{9}\)
-
C.
\(\dfrac{{ab}}{3}\)
-
D.
\(\dfrac{{ab}}{9}\)
Đáp án : B
- Đưa về cùng mặt phẳng.
- Dựng thiết diện dựa vào các yếu tố song song có trong giả thiết.
- Chứng minh thiết diện là hình chữ nhật giao đó tính diện tích hình chữ nhật đó.
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ICD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ICD} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) và $\left( {ICD} \right)$ là đường thẳng qua $M$ và song song với $CD$ cắt $IC$ tại $L$ và cắt $ID$ tại $N$.
Tương tự \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {JAB} \right)\\AB\parallel \left( \alpha \right)\\AB \subset \left( {JAB} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) và $\left( {JAB} \right)$ là đường thẳng qua $M$ và song song $AB$ cắt $JA$ tại $P$ và cắt $JB$ tại $Q$.
Ta có: \(\left\{ \begin{array}{l}L \in \left( \alpha \right) \cap \left( {ABC} \right)\\AB\parallel \left( \alpha \right)\\AB \subset \left( {ABC} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) với $\left( {ABC} \right)$ là đường thẳng qua $L$ song song với $AB$ cắt $BC$ tại $E$ và cắt $AC$ tại $F$ . Do đó $EF//AB{\rm{ }}\left( 1 \right)$
Tương tự \(\left\{ \begin{array}{l}N \in \left( \alpha \right) \cap \left( {ABD} \right)\\AB\parallel \left( \alpha \right)\\AB \subset \left( {ABD} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\)và $\left( {ABD} \right)$ là đường thẳng qua $N$ song song với $AB$ cắt $BD$ tại $H$ và cắt $AD$ tại $G$ .
Do đó $HG//AB\left( 2 \right)$ .
Từ (1) và (2) suy ra EF // HG // AB (*)
Ta có: $\left\{ \begin{array}{l}FG = \left( \alpha \right) \cap \left( {ACD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ACD} \right)\end{array} \right. \Rightarrow FG\parallel CD\,\,\,\left( 3 \right)$.
Tương tự \(\left\{ \begin{array}{l}EH = \left( \alpha \right) \cap \left( {BCD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {BCD} \right)\end{array} \right. \Rightarrow EH\parallel CD\,\,\left( 4 \right).\)
Từ (*) và (**) suy ra $EFGH$ là hình bình hành.
Mà \(AB \bot CD \Rightarrow EF \bot FG.\) Vậy thiết diện $EFGH$ là hình chữ nhật
\( \Rightarrow {S_{EFGH}} = EF.FG = PQ.LN.\)
Trong tam giác $JAB$, ta có \(\dfrac{{PQ}}{{AB}} = \dfrac{{JM}}{{JI}} = \dfrac{2}{3} \Rightarrow PQ = \dfrac{{2AB}}{3} = \dfrac{{2a}}{3}.\)
Trong tam giác $ICD$ ta có \(\dfrac{{LN}}{{CD}} = \dfrac{{IM}}{{IJ}} = \dfrac{1}{3} \Rightarrow LN = \dfrac{{CD}}{3} = \dfrac{b}{3}.\)
Vậy diện tích thiết diện là: \({S_{EFGH}} = \dfrac{{2a}}{3}.\dfrac{b}{3} = \dfrac{{2ab}}{9}.\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
-
A.
$(NOM)$ cắt $(OPM)$
-
B.
$(MON) // (SBC)$
-
C.
\(\left( {PON} \right) \cap \left( {MNP} \right) = NP\)
-
D.
\(\left( {MNP} \right)//\left( {SBD} \right)\)
Đáp án : B
\(\left\{ \begin{array}{l}a//\left( \beta \right)\\b//\left( \beta \right)\\a \cap b \subset \left( \alpha \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\) hoặc \(\left\{ \begin{array}{l}a//a'\\b//b'\\a \cap b \subset \left( \alpha \right)\\a',b' \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\)
Dễ dàng chứng minh được $MNOP $ là hình bình hành \( \Rightarrow M,N,O,P\) đồng phẳng \( \Rightarrow A,C\) sai.
Ta có : $MN$ là đường trung bình của tam giác $SAD$ \( \Rightarrow MN//AD//BC\)
$ON$ là đường trung bình của tam giác $SBD$ \( \Rightarrow ON//SB\)
\( \Rightarrow (MON) // (SBC)\)
\( \Rightarrow \) Đáp án B đúng.
Đáp án D sai vì \(N \in \left( {MNP} \right) \cap \left( {SBD} \right)\)
Cho hai hình vuông $ABCD,ABEF$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo $AC$ và $BF$ ta lấy các điểm $M, N$ sao cho $AM = BN.$ Mặt phẳng $(P)$ chứa $MN$ và song song với $AB$ cắt $AD$ và $AF$ lần lượt tại $M’, N’.$ Khẳng định nào sau đây là đúng?
-
A.
$AC, BF$ cắt nhau
-
B.
Tứ giác $MNM’N’$ là hình bình hành
-
C.
$MN$ song song với $(DEF)$
-
D.
$MN$ cắt $(DEF)$
Đáp án : C
+) Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
+) Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song
và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia.
Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
Ta có:
\(\left\{ \begin{array}{l}\dfrac{{AM'}}{{AD}} = \dfrac{{AM}}{{AC}}\\\dfrac{{AN'}}{{AF}} = \dfrac{{BN}}{{BF}}\\AM = BN;AC = BF\end{array} \right. \Rightarrow \dfrac{{AM'}}{{AD}} = \dfrac{{AN'}}{{AF}} \Rightarrow M'N'//DF\)
Lại có NN’ // AB // EF \( \Rightarrow \left( {MM'N'N} \right)//\left( {DEF} \right)\)
Mà \(MN \subset \left( {MM'N'N} \right) \Rightarrow MN//\left( {DEF} \right)\)
Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình thoi $\widehat {BAD} = {60^0}$ và $A'A = A'B = A'D$. Gọi $O = AC \cap BD$. Hình chiếu của $A'$ trên $\left( {ABCD} \right)$ là :
-
A.
trung điểm của $AO.$
-
B.
trọng tâm $\Delta ABD.$
-
C.
giao của hai đoạn $AC$ và $BD.$
-
D.
trọng tâm$\Delta BCD.$
Đáp án : B
Sử dụng định nghĩa trục đường tròn đáy để tìm hình chiếu của \(A'\) trên mặt đáy
Vì $A'A = A'B = A'D \Rightarrow $ hình chiếu của \(A'\) trên $\left( {ABCD} \right)$ trùng với \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABD\,\,\left( 1 \right).\)
Mà tứ giác \(ABCD\) là hình thoi và $\widehat {BAD} = {60^0}$ nên \(\Delta BAD\) là tam giác đều \(\left( 2 \right)\)
Từ \(\left( 1 \right)\,\)và \(\left( 2 \right) \Rightarrow H\) là trọng tâm \(\Delta ABD\,.\)
Cho tam giác \(ABC\) vuông cân tại \(A\) và \(BC = a.\) Trên đường thẳng qua \(A\) vuông góc với \(\left( {ABC} \right)\) lấy điểm \(S\) sao cho $SA = \dfrac{{a\sqrt 6 }}{2}$. Tính số đo góc giữa đường thẳng \(SA\) và \(\left( {ABC} \right)\)
-
A.
\(30^\circ \).
-
B.
\(45^\circ \).
-
C.
\(60^\circ \).
-
D.
\(90^\circ \).
Đáp án : D
\(SA \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = 90^\circ \).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Đường thẳng $SO$ vuông góc với mặt phẳng đáy $\left( {ABCD} \right)$ và $SO = \dfrac{{a\sqrt 3 }}{2}$. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$.
-
A.
${30^0}.$
-
B.
${45^0}.$
-
C.
${60^0}.$
-
D.
${90^0}.$
Đáp án : C
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Gọi \(Q\) là trung điểm \(BC\), suy ra \(OQ \bot BC\).
Ta có $\left\{ \begin{array}{l}BC \bot OQ\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOQ} \right) \Rightarrow BC \bot SQ.$
Do đó
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SQ \bot BC\\\left( {ABCD} \right) \supset OQ \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SQ;OQ} \right)} = \widehat {SQO}.$
Tam giác vuông $SOQ$, có $\tan \widehat {SQO} = \dfrac{{SO}}{{OQ}} = \sqrt 3 \Rightarrow \widehat {SQO} = {60^0}$
Vậy mặt phẳng $\left( {SBC} \right)$ hợp với mặt đáy $\left( {ABCD} \right)$ một góc ${60^0}.$
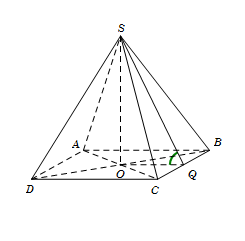
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $I$, cạnh $a$, góc $\widehat {BAD} = {60^0}$, $SA = SB = SD = \dfrac{{a\sqrt 3 }}{2}$. Gọi \(\varphi \) là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right).$ Mệnh đề nào sau đây đúng?
-
A.
$\tan \varphi = \sqrt 5 .$
-
B.
$\tan \varphi = \dfrac{{\sqrt 5 }}{5}.$
-
C.
$\tan \varphi = \dfrac{{\sqrt 3 }}{2}.$
-
D.
$\varphi = {45^0}.$
Đáp án : A
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Từ giả thiết suy ra tam giác $ABD$ đều cạnh $a$.
Gọi $H$ là hình chiếu của $S$ trên mặt phẳng $\left( {ABCD} \right)$.
Do $SA = SB = SD$ nên suy ra $H$ là tâm của tam gác đều $ABD$.
Suy ra $AH = \dfrac{2}{3}AI = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3},HI = \dfrac{1}{3}AI = \dfrac{1}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}$
và $SH = \sqrt {S{A^2} - A{H^2}} = \dfrac{{a\sqrt {15} }}{6}.$
Vì $ABCD$ là hình thoi nên $HI \bot BD$. Tam giác $SBD$ cân tại $S$ nên $SI \bot BD$. Do đó $\widehat {\left( {SBD} \right);\left( {ABCD} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIH}.$.
Trong tam vuông $SHI$, có $\tan \widehat {SIH} = \dfrac{{SH}}{{HI}} = \sqrt 5 .$

Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.
-
A.
$1.$
-
B.
$\sqrt 2 .$
-
C.
$2.$
-
D.
$4.$
Đáp án : C
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng
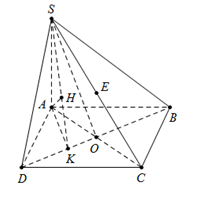
Ta có $E \in SC$, $EC \cap \left( {SBD} \right) = S \Rightarrow \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{ES}}{{CS}} = \dfrac{1}{2}$
Từ A kẻ $ AK \bot BD\left( {K \in BD} \right)$, kẻ $AH \bot SK\,\,\left( {H \in SK} \right)\,\,\,\,\,\,\left( 1 \right)$.
Ta có: \(\left\{ \begin{array}{l}BD \bot AK\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAK} \right) \Rightarrow BD \bot AH\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AH \bot \left( {SBD} \right).\)
$ \Rightarrow AH = d\left( {A;\left( {SBD} \right)} \right) = 2.d\left( {E;\left( {SBD} \right)} \right) = \dfrac{{2a}}{3}.$
Mà $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{K^2}}} \Rightarrow AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} - A{H^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$.
Tam giác $ABD$ vuông tại $A$, có đường cao $AK$.
$ \Rightarrow \dfrac{1}{{A{B^2}}} + \dfrac{1}{{AD{}^2}} = \dfrac{1}{{A{K^2}}} \Leftrightarrow \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}{x^2}}} = \dfrac{5}{{4{a^2}}} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{x^2} = 4\end{array} \right. \Rightarrow x = 2$
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
-
A.
\(d = a\sqrt 3 .\)
-
B.
\(d = 5a\sqrt 3 .\)
-
C.
\(d = \dfrac{{5a}}{2}.\)
-
D.
\(d = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
Đáp án : D
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng
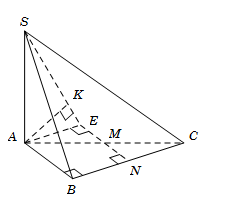
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 5a\)
Xác định \({60^0} = \widehat {\left( {SC,\left( {ABC} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA}\) và \(SA = AC.\tan \widehat {SCA} = 5a\sqrt 3 .\)
Gọi \(N\) là trung điểm \(BC\), suy ra \(MN\parallel AB\).
Lấy điểm \(E\) đối xứng với \(N\) qua \(M\), suy ra \(ABNE\) là hình chữ nhật.
Do đó $d\left( {AB;SM} \right) = d\left( {AB;\left( {SME} \right)} \right) = d\left( {A;\left( {SME} \right)} \right).$
Kẻ \(AK \bot SE\).
Vì \(ME \bot AE,ME \bot SA\) nên \(ME \bot \left( {SAE} \right) \Rightarrow ME \bot AK\)
Mà \(AK \bot SE\) nên \(AK \bot \left( {SME} \right)\)
Khi đó \(d\left( {A;\left( {SME} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
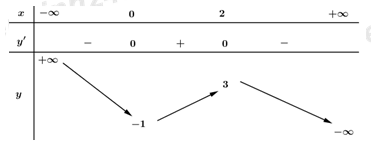
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

Hàm số đạt cực đại tại điểm:
-
A.
$x = 2$
-
B.
$x = 0$
-
C.
$x = 3$
-
D.
$x = - 1$
Đáp án : A
+) Hàm số đạt điểm cực trị tại $x = {x_0}$ khi $x = {x_0}$ là nghiệm của phương trình $y' = 0$ .
+) Hàm số đạt cực đại tại $x = {x_0}$ khi tại $x = {x_0}$ hàm số đổi dấu từ dương sang âm.
Dựa vào đồ thị hàm số ta thấy hàm số đạt cực đại tại điểm $x = 2.$
Tiếp tuyến kẻ từ điểm $\left( {2;3} \right)$ tới đồ thị hàm số $y = \dfrac{{3x + 4}}{{x - 1}}$ là
-
A.
$y = - 28x + 59$ ; $y = x + 1$.
-
B.
$y = -24x + 51$; $y = x + 1$.
-
C.
$y = - 28x + 59$.
-
D.
$y = - 28x + 59$; $y = - 24x + 51$.
Đáp án : C
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({x_0}\,\,\left( d \right)\)
Cho \(M \in \left( d \right)\), tìm \({x_0}\)
$y = \dfrac{{3x + 4}}{{x - 1}} \Rightarrow y' = \dfrac{{ - 7}}{{{{\left( {x - 1} \right)}^2}}}$.
Phương trình tiếp tuyến của đồ thị $\left( C \right):y = \dfrac{{3x + 4}}{{x - 1}}$ tại điểm \(M\left( {{x_0};{y_0}} \right) \in \left( C \right)\) với \({x_0} \ne 2\) là:
\(y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\)\( \Leftrightarrow y = \dfrac{{ - 7}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{3{x_0} + 4}}{{{x_0} - 1}}\).
Vì tiếp tuyến đi qua điểm $\left( {2;\,3} \right)$ nên ta có \(3 = \dfrac{{ - 7}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {2 - {x_0}} \right) + \dfrac{{3{x_0} + 4}}{{{x_0} - 1}}\)\( \Leftrightarrow {x_0} = \dfrac{3}{2}\).
Vậy có một tiếp tuyến thỏa đề bài là: $y = -28x + 59$.
Cho hàm số \(f\left( x \right) = - 4{x^3} + 4x - 1.\) Mệnh đề nào sau đây là sai?
-
A.
Hàm số đã cho liên tục trên \(\mathbb{R}.\)
-
B.
Phương trình \(f\left( x \right) = 0\) không có nghiệm trên khoảng \(\left( { - \infty ;1} \right).\)
-
C.
Phương trình \(f\left( x \right) = 0\) có nghiệm trên khoảng \(\left( { - 2;0} \right).\)
-
D.
Phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm trên khoảng \(\left( { - 3;\dfrac{1}{2}} \right).\)
Đáp án : B
Xét tính đúng sai của từng đáp án và kết luận.
(i) Hàm \(f\left( x \right)\) là hàm đa thức nên liên tục trên \(\mathbb{R}\) nên A đúng.
(ii) Ta có \(\left\{ \begin{array}{l}f\left( { - 1} \right) = - 1 < 0\\f\left( { - 2} \right) = 23 > 0\end{array} \right. \Rightarrow f\left( x \right) = 0\) có nghiệm \({x_1}\) trên \(\left( { - 2;1} \right)\), mà $\left( { - 2; - 1} \right) \subset \left( { - 2;0} \right) \subset \left( { - \infty ;1} \right)$ nên B sai và C đúng.
(iii) Ta có \(\left\{ \begin{array}{l}f\left( 0 \right) = - 1 < 0\\f\left( {\dfrac{1}{2}} \right) = \dfrac{1}{2} > 0\end{array} \right. \Rightarrow f\left( x \right) = 0\) có nghiệm \({x_2}\) thuộc \(\left( {0;\dfrac{1}{2}} \right).\) Kết hợp với (1) suy ra \(f\left( x \right) = 0\) có các nghiệm \({x_1},\,\,{x_2}\) thỏa: \( - 3 < {x_1} < - 1 < 0 < {x_2} < \dfrac{1}{2}\) nên D đúng.
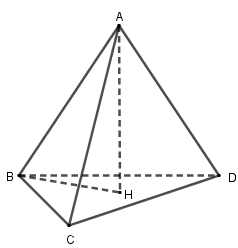
Cho tứ diện \(ABCD\) có \(AB \bot CD\) và \(AC \bot BD\). Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(mp(BCD)\). Chọn khẳng định đúng :
-
A.
\(H\) là trọng tâm tam giác \(BCD\).
-
B.
\(CD \bot (ACH)\).
-
C.
\(AD \bot BC\).
-
D.
Các khẳng định trên đều đúng.
Đáp án : C
Ta có \(\left\{ \begin{array}{l}CD \bot AB\\CD \bot AH\end{array} \right. \Rightarrow CD \bot (ABH) \Rightarrow CD \bot BH\). Tương tự \(BD \bot CH\)
Suy ra \(H\) là trực tâm \(\Delta BCD\). Suy ra đáp án A, B, D sai.
Ta có \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot DH\end{array} \right. \Rightarrow BC \bot AD\), suy ra C đúng.
\( \to \) Chọn đáp án C.
Cho hình chóp \(S.ABC\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tâm \(O\). Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(\varphi \) là góc giữa \(SO\) và mặt phẳng \(\left( {ABCD} \right)\). Mệnh đề nào sau đây đúng?
-
A.
\(\tan \varphi = 2\sqrt 2 .\)
-
B.
\(\varphi = {60^0}.\)
-
C.
\(\tan \varphi = 2.\).
-
D.
\(\varphi = {45^0}.\)
Đáp án : A
Bước 1: Tìm hình chiếu vuông góc của \(SO\) trên mặt đáy rồi suy ra góc giữa đường thẳng \(SO\) và mặt phẳng đáy.
Sử dụng lý thuyết:
Góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Bước 2: Tính góc ở trên dựa vào các tỉ số lượng giác trong tam giác vuông.
Bước 1:
Vì \(SA \bot \left( {ABCD} \right)\) nên hình chiếu vuông góc của \(SO\) trên mặt đáy \(\left( {ABCD} \right)\) là \(AO\).
Do đó \(\widehat {\left( {SO,\left( {ABCD} \right)} \right)} = \widehat {\left( {SO,OA} \right)} = \widehat {SOA}.\)
Bước 2:
Trong tam giác vuông \(SAO\), ta có \(\tan \widehat {SOA} = \dfrac{{SA}}{{OA}} = 2\sqrt 2 .\)
Vậy \(SO\) hợp với mặt đáy \(\left( {ABCD} \right)\) một góc nhọn \(\varphi \) thỏa mãn \(\tan \varphi = 2\sqrt 2 \).
Đồ thị hàm số \(y = \tan x\) nhận đường thẳng nào sau đây là tiệm cận?
-
A.
\(y = \dfrac{\pi }{3} + k\pi \left( {k \in Z} \right)\)
-
B.
\(x = k\pi \left( {k \in Z} \right)\)
-
C.
\(x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
-
D.
\(y = \dfrac{{k\pi }}{2}\left( {k \in Z} \right)\)
Đáp án : C
Sử dụng tiệm cận của đồ thị hàm số \(y = \tan x\).
Đồ thị hàm số \(y = \tan x\) nhận các đường thẳng \(x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\) làm tiệm cận đứng.
Một số em có thể sẽ chọn nhầm đáp án A vì nhìn nhầm thành \(x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\) là sai.
Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau
\(y = 3{\left( {3\sin x + 4\cos x} \right)^2} + 4\left( {3\sin x + 4\cos x} \right) + 1\)
-
A.
\(\min y = \dfrac{1}{3};\max y = 96\)
-
B.
\(\min y = \dfrac{1}{3};\max y = 6\)
-
C.
\(\min y = - \dfrac{1}{3};\max y = 96\)
-
D.
\(\min y = 2;\max y = 6\)
Đáp án : C
- Đặt \(t = 3.\sin x + 4.\cos x\) và tìm điều kiện của \(t\).
- Tìm GTNN của hàm số theo \(t\) và kết luận.
Đặt \(t = 3.\sin x + 4.\cos x\), theo bất đẳng thức Bunhiacopxki, ta có:
$\begin{array}{l}
{t^2} = {\left( {3\sin x + 4\cos x} \right)^2}\\
\le \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\\
= 25.1 = 25\\
\Rightarrow {t^2} \le 25 \Rightarrow - 5 \le t \le 5
\end{array}$
Xét hàm số \(y = 3{t^2} + 4t + 1 \) trên \([-5;5]\).
Hàm số \(y = 3{t^2} + 4t + 1 \) là hàm bậc hai có:
$\begin{array}{l}
- \frac{b}{{2a}} = - \frac{2}{3} \in \left[ { - 5;5} \right]\\
y\left( { - \frac{2}{3}} \right) = - \frac{1}{3}\\
y\left( { - 5} \right) = 56\\
y\left( 5 \right) = 96
\end{array}$
Ta có bảng biến thiên:
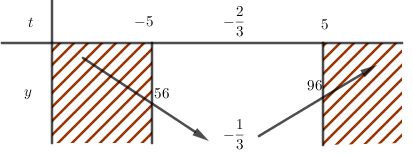
\( \Rightarrow \min y = - \dfrac{1}{3}\) khi \(t=- \dfrac{1}{3}\)
\(\max y = 96\) khi \(t=5\).
Trên giá sách có $6$ quyển Văn khác nhau, $5$ quyển sách Toán khác nhau và $9$ quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?
-
A.
$54$
-
B.
$405$
-
C.
$30$
-
D.
$129$
Đáp án : D
+) Xét từng trường hợp:
- Có \(1\) quyển Văn và \(1\) quyển Toán: sử dụng quy tắc nhân.
- Có \(1\) quyển Toán và \(1\) quyển Tiếng Anh: sử dụng quy tắc nhân.
- Có \(1\) quyển Văn và \(1\) quyển Tiếng Anh: sử dụng quy tắc nhân.
+) Sử dụng quy tắc cộng để tính số cách chọn hai quyển sách khác nhau.
Theo quy tắc nhân ta có:
$6.5 = 30$ cách chọn một quyển Văn và một quyển Toán khác nhau.
$6.9 = 54$ cách chọn một quyển Văn và một quyển Tiếng Anh khác nhau.
$5.9 = 45$ cách chọn một quyển Toán và một quyển Tiếng Anh khác nhau.
Theo quy tắc cộng ta có số cách chọn hai quyển sách khác môn là: $30 + 54 + 45 = 129$ cách.
Để phương trình \({\sin ^2}x + 2\left( {m + 1} \right)\sin x - 3m\left( {m - 2} \right) = 0\) có nghiệm, các giá trị của tham số m là:
-
A.
\(\left[ \begin{array}{l} - \dfrac{1}{2} \le m \le \dfrac{1}{2}\\1 \le m \le 2\end{array} \right.\)
-
B.
\(\left[ \begin{array}{l} - \dfrac{1}{3} \le m \le \dfrac{1}{3}\\1 \le m \le 3\end{array} \right.\)
-
C.
\(\left[ \begin{array}{l} - 2 \le m \le - 1\\0 \le m \le 1\end{array} \right.\)
-
D.
\(\left[ \begin{array}{l} - 1 \le m \le 1\\3 \le m \le 4\end{array} \right.\)
Đáp án : B
Đặt \(\sin x = t\,\,\left( { - 1 \le t \le 1} \right)\), tìm điều kiện để phương trình ẩn \(t\) có nghiệm trong đoạn \(\left[ { - 1;1} \right]\).
\({\sin ^2}x + 2\left( {m + 1} \right)\sin x - 3m\left( {m - 2} \right) = 0\,\,\,\left( * \right)\)
Đặt \(\sin x = t\,\,\left( { - 1 \le t \le 1} \right)\) khi đó phương trình có dạng \({t^2} + 2\left( {m + 1} \right)t - 3m\left( {m - 2} \right) = 0\,\,\,\left( 1 \right)\)
Ta có: \(\Delta ' = {\left( {m + 1} \right)^2} + 3m\left( {m - 2} \right) = 4{m^2} - 4m + 1 = {\left( {2m - 1} \right)^2} \ge 0\,\,\forall m \in R\)
TH1: \(\Delta ' = 0 \Leftrightarrow m = \dfrac{1}{2}\) phương trình (1) có nghiệm \(t = - m - 1 = \dfrac{{ - 1}}{2} - 1 = - \dfrac{3}{2}\,\,\left( {ktm} \right)\)
TH2: \(\Delta ' > 0 \Leftrightarrow m \ne \dfrac{1}{2}\). Khi đó phương trình có 2 nghiệm
\(\left[ \begin{array}{l}{t_1} = - m - 1 + 2m - 1 = m - 2\\{t_2} = - m - 1 - 2m + 1 = - 3m\end{array} \right.\)
Để phương trình (*) có nghiệm thì phương trình (1) có nghiệm \( - 1 \le t \le 1\)
\( \Leftrightarrow \left[ \begin{array}{l} - 1 \le m - 2 \le 1\\ - 1 \le - 3m \le 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}1 \le m \le 3\\ - \dfrac{1}{3} \le m \le \dfrac{1}{3}\end{array} \right.\)
Nghiệm của phương trình \(\cos 7x\cos 5x - \sqrt 3 \sin 2x = 1 - \sin 7x\sin 5x\) là:
-
A.
$\left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
-
B.
$\left[ \begin{array}{l}x = k\pi \\x = - \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
-
C.
$x = k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)$
-
D.
$\left[ \begin{array}{l}x = k2\pi \\x = - \dfrac{\pi }{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
Đáp án : B
Bước 1: Đưa về phương trình $a.\sin x+b.\cos x=c$
Bước 2: Chia cả 2 vế cho $\sqrt{a^2+b^2}$ và đưa về phương trình lượng giác cơ bản
Sử dụng công thức \(\cos a\cos b - \sin a\sin b = \cos \left( {a + b} \right)\)
Bước 3: Giải phương trình lượng giác
Sử dụng công thức \(\cos x = \cos y \Leftrightarrow x = \pm y + k2\pi \)
Bước 1:
$\begin{array}{l}\cos 7x\cos 5x - \sqrt 3 \sin 2x = 1 - \sin 7x\sin 5x\\ \Leftrightarrow \cos 7x\cos 5x + \sin 7x\sin 5x - \sqrt 3 \sin 2x = 1\\ \Leftrightarrow \cos \left( {7x - 5x} \right) - \sqrt 3 \sin 2x = 1\\ \Leftrightarrow \cos 2x - \sqrt 3 \sin 2x = 1\end{array}$
Bước 2:
$ \Leftrightarrow \dfrac{1}{2}\cos 2x - \dfrac{{\sqrt 3 }}{2}\sin 2x = \dfrac{1}{2}\\ \Leftrightarrow \cos 2x\cos \dfrac{\pi }{3} - \sin 2x\sin \dfrac{\pi }{3} = \cos \dfrac{\pi }{3}\\ \Leftrightarrow \cos \left( {2x + \dfrac{\pi }{3}} \right) = \cos \dfrac{\pi }{3}$
Bước 3:
$\Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{3} + k2\pi \\2x + \dfrac{\pi }{3} = - \dfrac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = - \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$
Giá trị của $n$ thỏa mãn $3A_n^2 - A_{2n}^2 + 42 = 0$ là
-
A.
$9$.
-
B.
$8$.
-
C.
$6$.
-
D.
$10$.
Đáp án : C
Sử dụng công thức \(A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}}\) thay vào giải phương trình ẩn \(n\)
* PP tự luận:
+ PT \( \Leftrightarrow 3.\dfrac{{n!}}{{\left( {n - 2} \right)!}} - \dfrac{{\left( {2n} \right)!}}{{\left( {2n - 2} \right)!}} + 42 = 0\,\,,\,\,\left( {n \in \mathbb{N},n \ge 2} \right)\)\( \Leftrightarrow 3n\left( {n - 1} \right) - 2n.\left( {2n - 1} \right) + 42 = 0\)\( \Leftrightarrow - {n^2} - n + 42 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = 6\,\left( {TM} \right)\\n = - 7\,\left( L \right)\end{array} \right.\)\( \Leftrightarrow n = 6\).
+ Nhập vào máy tính PT $3A_n^2 - A_{2n}^2 + 42 = 0$.
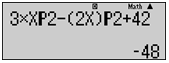
Tính (CALC) lần lượt với \(X = 9\) (không thoả); với \(X = 8\) (không thoả), với \(X = 6\) (thoả), với \(X = 10\) (không thoả).

Một con xúc sắc cân đối và đồng chất được gieo ba lần. Gọi $P$ là xác suất để tổng số chấm xuất hiện ở hai lần gieo đầu bằng số chấm xuất hiện ở lần gieo thứ ba. Khi đó $P$ bằng:
-
A.
$\dfrac{{10}}{{216}}$.
-
B.
$\dfrac{{15}}{{216}}$.
-
C.
$\dfrac{{16}}{{216}}$.
-
D.
$\dfrac{{12}}{{216}}$.
Đáp án : B
- Tính số phần tử của không gian mẫu \(n\left( \Omega \right)\).
- Liệt kê các khả năng có lợi cho biến cố.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
$n(\Omega ) = 6.6.6 = 216$. Gọi $A$:”tổng số chấm xuất hiện ở hai lần gieo đầu bằng số chấm xuất hiện ở lần gieo thứ ba”.
Ta chỉ cần chọn 1 bộ 2 số chấm ứng với hai lần gieo đầu sao cho tổng của chúng thuộc tập $\{ 1;2;3;4;5;6\} $ và số chấm lần gieo thứ ba sẽ là tổng hai lần gieo đầu.
Liệt kê ra ta có:
${\rm{\{ (1;1);(1;2);(1;3);(1;4);(1;5);(2;1);(2;2);(2;3);(2;4);(3;1);(3;2);(3;3);(4;1);(4;2);(5;1)\} }}$
Do đó $n(A) = 15$. Vậy $P(A) = \dfrac{{15}}{{216}}$.
Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
-
A.
$5.2500.000$ đồng
-
B.
$10.125.000$ đồng
-
C.
$4.000.000$ đồng
-
D.
$4.245.000$ đồng
Đáp án : B
Sử dụng công thức \({S_n} = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}\).
Giá tiền khoan mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 80\,000,\,\,d = 5\,000.\)
Do cần khoan 50 mét nên tổng số tiền cần trả là
\({u_1} + {u_2} + \cdots + {u_{50}} = {S_{50}} = 50{u_1} + \dfrac{{50.49}}{2}d\) \( = 50.80\,000 + 1225.5\,000 = 10\,125\,000\)
Trong các dãy số $\left( {{u_n}} \right)$ cho bởi số hạng tổng quát ${u_n}$ sau, dãy số nào là một cấp số nhân?
-
A.
\({u_n} = 7 - 3n.\)
-
B.
\({u_n} = 7 - {3^n}.\)
-
C.
\({u_n} = \dfrac{7}{{3n}}.\)
-
D.
\({u_n} = {7.3^n}.\)
Đáp án : D
Nhận xét dạng của các số hạng \({u_n}\) ở mỗi đáp án và kết luận.
Dãy \({u_n} = {7.3^n}\) là cấp số nhân có \(\left\{ \begin{array}{l}{u_1} = 21\\q = 3\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 - 4t\\y = 1 + t\end{array} \right..\)Ảnh của đường thẳng \(\Delta \) qua phép đối xứng tâm \(I\left( { - 2;2} \right)\) có phương trình là:
-
A.
\(x + 4y - 5 = 0.\)
-
B.
\(x + 4y - 6 = 0.\)
-
C.
$4x - y + 1 = 0.$
-
D.
\(4x - y - 1 = 0.\)
Đáp án : B
- Đưa \(\Delta \) về phương trình tổng quát.
- Sử dụng biểu thức tọa độ của phép đối xứng tâm \(I\left( {a;b} \right)\) là $\left\{ {\begin{array}{*{20}{c}}{x' = 2a - x}\\{y' = 2b - y}\end{array}} \right.$
- Rút \(x,y\) theo \(x',y'\) và thay vào phương trình của \(\Delta \) suy ra phương trình mới.
Đường thẳng \(\Delta \) có phương trình tổng quát là \(x + 4y - 6 = 0.\)
Biểu thức tọa độ của phép đối xứng tâm \(I\left( {a;b} \right)\) là $\left\{ {\begin{array}{*{20}{c}}{x' = 2a - x}\\{y' = 2b - y}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 4 - x'}\\{y = 4 - y'}\end{array}} \right..$
Thay vào phương trình đường thẳng \(d\) ta được \(\left( { - 4 - x'} \right) + 4\left( {4 - y'} \right) - 6 = 0\)
\( \Leftrightarrow x' + 4y' - 6 = 0\).
Cách 2. Nhận thấy \(I\left( { - 2;2} \right) \in \Delta \) nên ảnh của đường thẳng $\Delta $ qua phép đối xứng tâm \(I\)trùng với chính nó. Vậy ảnh của đường thẳng \(\Delta \) qua phép đối xứng tâm \(I\left( { - 2;2} \right)\) có phương trình là: \(x + 4y - 6 = 0\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).

-
A.
\(13\)
-
B.
$11$
-
C.
$10$
-
D.
$12$
Đáp án : D
Xác định số điểm mà đạo hàm đổi dấu của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).
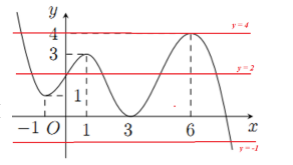
Ta có: \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}} \Rightarrow y' = {2019^{f\left( {f\left( x \right) - 1} \right)}}.f'\left( {f\left( x \right) - 1} \right).f'\left( x \right)\ln 2019\)
\(f'\left( {f\left( x \right) - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) - 1 = - 1\\f\left( x \right) - 1 = 1\\f\left( x \right) - 1 = 3\\f\left( x \right) - 1 = 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 2\\f\left( x \right) = 4\\f\left( x \right) = 7\end{array} \right.\)
\(f'\left( {f\left( x \right) - 1} \right) = 0\) có tất cả: \(2 + 5 + 2 + 1 = 10\) nghiệm
(trong đó, có các nghiệm \(x = 3,\,\,x = 6\) là nghiệm kép, còn lại là nghiệm đơn).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 3\\x = 6\end{array} \right.\) : có 4 nghiệm
\( \Rightarrow y' = {2019^{f\left( {f\left( x \right) - 1} \right)}}.f'\left( {f\left( x \right) - 1} \right).f'\left( x \right) = 0\) có 12 nghiệm phân biệt, trong đó, \(x = 3,\,\,x = 6\) là nghiệm bội 3, còn lại là nghiệm đơn.
Do đó, số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\) là 12.
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
-
A.
\(1\).
-
B.
\(\dfrac{1}{3}\).
-
C.
\(\dfrac{2}{3}\).
-
D.
\(\dfrac{1}{2}\).
Đáp án : D
Tính \(n\left( \Omega \right)\) và \(n\left( A \right)\) suy ra xác suất \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Số phần tử không gian mẫu \(n\left( \Omega \right) = 6\).
Gọi biến cố A: “mặt chẵn chấm xuất hiện”
Ta có: \(A = \left\{ {2;4;6} \right\} \Rightarrow n\left( A \right) = 3\).
Vậy xác suất \(P\left( A \right) = \dfrac{3}{6} = \dfrac{1}{2}\).
Cho tứ diện \(ABCD\) có \(AB = CD = 4,BC = AD = 5,AC = BD = 6\). \(M\) là điểm thay đổi trong tâm giác \(ABC\). Các đường thẳng qua \(M\) song song với \(AD,BD,CD\) tương ứng cắt mặt phẳng \(\left( {BCD} \right),\left( {ACD} \right),\left( {ABD} \right)\) tại \(A',B',C'\). Giá trị lớn nhất của \(MA'.MB'.MC'\) là
-
A.
\(\dfrac{{40}}{9}\)
-
B.
\(\dfrac{{24}}{9}\)
-
C.
\(\dfrac{{30}}{9}\)
-
D.
\(\dfrac{{20}}{9}\)
Đáp án : A
- Kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
- Dựng các đường thẳng qua \(M\) và song song với \(AD,BD,CD\) suy ra các điểm \(A',B',C'\).
- Sử dụng định lý Ta – let tính \(MA',MB',MC'\).
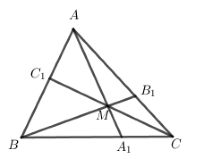
- Sử dụng hệ thức \(\dfrac{{{A_1}M}}{{AM}} + \dfrac{{{B_1}M}}{{BM}} + \dfrac{{{C_1}M}}{{CM}} = 1\) đánh giá GTLN của tích \(MA'.MB'.MC'\).
ở đó, \(M\) là một điểm nằm trong tam giác \(ABC\) và \({A_1},{B_1},{C_1}\) lần lượt là các giao điểm của \(AM,BM,CM\) với các cạnh \(BC,CA,AB\).
Trong tam giác \(ABC\), kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
+) Trong mặt phẳng \(\left( {HAD} \right)\), kẻ \(MA'//AD\).
+) Trong mặt phẳng \(\left( {GBD} \right)\), kẻ \(MB'//BD\).
+) Trong mặt phẳng \(\left( {FCD} \right)\), kẻ \(MC'//CD\).
Từ đó ta được các điểm \(A',B',C'\) cần tìm.
Theo định lý Ta – let ta có: \(\dfrac{{MA'}}{{AD}} = \dfrac{{HM}}{{HA}} \Rightarrow MA' = 5.\dfrac{{MH}}{{AH}}\)
\(\dfrac{{MB'}}{{BD}} = \dfrac{{GM}}{{GB}} \Rightarrow MB' = 6.\dfrac{{MG}}{{BG}}\); \(\dfrac{{MC'}}{{CD}} = \dfrac{{FM}}{{FC}} \Rightarrow MC' = 4.\dfrac{{MF}}{{CF}}\)
\( \Rightarrow MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}\).
Trong tam giác \(ABC\) ta có: \(1 = \dfrac{{MH}}{{AH}} + \dfrac{{MG}}{{BG}} + \dfrac{{MF}}{{CF}} \ge 3\sqrt[3]{{\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}}}\) \( \Rightarrow \dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le \dfrac{1}{{27}}\)
Do đó \(MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le 120.\dfrac{1}{{27}} = \dfrac{{40}}{9}\)\( \Rightarrow {\left( {MA'.MB'.MC'} \right)_{\max }} = \dfrac{{40}}{9}\)
Cho hàm số \(f\left( x \right)\) có bảng xét dấu có đạo hàm như hình bên dưới
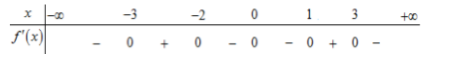
Hàm số \(y = f\left( {1 - 2x} \right)\) đồng biến trên khoảng
-
A.
\(\left( {0;\dfrac{3}{2}} \right)\)
-
B.
\(\left( { - \dfrac{1}{2};1} \right)\)
-
C.
\(\left( { - 2; - \dfrac{1}{2}} \right)\)
-
D.
\(\left( {\dfrac{3}{2};3} \right)\)
Đáp án : A
Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {a;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.
Ta có: \(y' = - 2f'\left( {1 - 2x} \right)\).
Với \(x = 1 \Rightarrow y'\left( 1 \right) = - 2f'\left( { - 1} \right) > 0 \Rightarrow \) Loại đáp án B, C, D.
Ngoài phương pháp thử HS có thể lập BXD \(y'\), tuy nhiên trong bài tập này, thử là phương pháp tối ưu nhất.
Cách tự luận:
\(\begin{array}{l}y' > 0 \Leftrightarrow - 2f'\left( {1 - 2x} \right) > 0\\ \Leftrightarrow f'\left( {1 - 2x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}1 - 2x < - 3\\ - 2 < 1 - 2x < 0\\0 < 1 - 2x < 1\\1 - 2x > 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\frac{1}{2} < x < \frac{3}{2}\\0 < x < \frac{1}{2}\\x < - 1\end{array} \right.\end{array}\)
Nên hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {0;\frac{3}{2}} \right),\left( {2; + \infty } \right)\)
(trong khoảng \(\left( {0;\frac{3}{2}} \right)\) chứa điểm \(x = \frac{1}{2}\) làm cho đạo hàm \(f'\left( {1 - 2x} \right) = 0\) vẫn được)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận