Đề khảo sát chất lượng đầu năm Toán 12 - Đề số 1
Đề bài
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
-
A.
${x_0}$ là điểm cực đại của hàm số.
-
B.
${x_0}$ là điểm cực tiểu của hàm số.
-
C.
${x_0}$ là điểm cực đại của đồ thị hàm số.
-
D.
${x_0}$ là điểm cực tiểu của đồ thị hàm số.
Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ có cực đại và cực tiểu.
-
A.
$0 < m \leqslant 1.$
-
B.
$\left[ \begin{gathered}m < 0 \hfill \\m > 1 \hfill \\ \end{gathered} \right.$
-
C.
$0 < m < 1.$
-
D.
$m < 0.$
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
-
A.
$f\left( 0 \right) < 5$
-
B.
$f\left( 2 \right) \geqslant 5$
-
C.
$f\left( 1 \right) = 5$
-
D.
$f\left( 0 \right) = 5$
Gieo đồng xu hai lần liên tiếp. Biến cố \(A\) là biến cố “Mặt ngửa xuất hiện đúng 1 lần”. Số phần tử của \({\Omega _A}\) là:
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(3\)
-
D.
\(4\)
Số đo bốn góc của một tứ giác lồi lập thành một cấp số nhân, biết rằng số đo của góc lớn nhất gấp $8$ lần số đo của góc nhỏ nhất. Tìm góc lớn nhất:
-
A.
${190^0}$
-
B.
${191^0}$
-
C.
${192^0}$
-
D.
${193^0}$
Từ các chữ số $1,2,3,4,5,6,7$ lập được bao nhiêu số tự nhiên gồm $4$ chữ số khác nhau và là số chẵn?
-
A.
$360$
-
B.
$343$
-
C.
$523$
-
D.
$347$
Giá trị của biểu thức \(S = {9^{99}}C_{99}^0 + {9^{98}}C_{99}^1 + {9^{97}}C_{99}^2 + ... + 9C_{99}^{98} + C_{99}^{99}\)\(\) bằng:
-
A.
\({10^{98}}\)
-
B.
\({10^{100}}\)
-
C.
\({10^{99}}\)
-
D.
Đáp án khác
Nghiệm của phương trình \({\sin ^2}x-\sin x = 0\) thỏa điều kiện: \(0 < x < \pi \).
-
A.
\(x = \dfrac{\pi }{2}\).
-
B.
\(x = \pi \).
-
C.
\(x = 0\).
-
D.
\(x = - \dfrac{\pi }{2}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}}\,\,khi\,\,x \ne 3\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 3\end{array} \right.\). Tìm tất cả các giá trị của tham số thực $m$ để hàm số liên tục tại $x = 3.$
-
A.
\(m \in \emptyset \)
-
B.
\(m \in R\)
-
C.
$m = 1$
-
D.
\(m = - 1\)
Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y = {x^4} + 2{x^2} - 1$ trên đoạn $\left[ { - 1;2} \right]$ lần lượt là $M$ và $m$. Khi đó giá trị của $M.m$ là:
-
A.
$ - 2$
-
B.
$46$
-
C.
$ - 23$
-
D.
$23$
Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = \left( {x -1}\right)\left({{x^2}- 2} \right)\left( {{x^4} - 4} \right)$. Số điểm cực trị của hàm số $y = f\left( x \right)$ là:
-
A.
$3$
-
B.
$2$
-
C.
$4$
-
D.
$1$
Nghiệm của phương trình \(\sin 3x = \cos x\) là:
-
A.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2},x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
-
B.
\(x = k2\pi ,x = \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
C.
\(x = k\pi ,x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
-
D.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2},x = - \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên trên khoảng $\left( {0;2} \right)$ như sau:
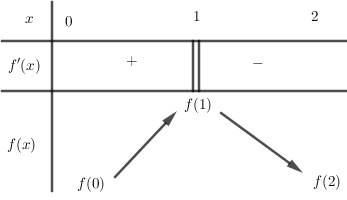
Khẳng định nào sau đây là khẳng định đúng:
-
A.
Trên $\left( {0;2} \right)$, hàm số không có cực trị
-
B.
Hàm số đạt cực đại tại $x = 1$
-
C.
Hàm số đạt cực tiểu tại $x = 1$
-
D.
Hàm số đạt cực tiểu tại $x = 0$
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y = \sqrt {2\sin x + 3} \)
-
A.
\(\max y = \sqrt 5 ,\min y = 1\)
-
B.
\(\max y = \sqrt 5 ,\min y = 0\)
-
C.
\(\max y = \sqrt 5 ,\min y = \sqrt 3 \)
-
D.
\(\max y = \sqrt 5 ,\min y = 3\)
Trong mặt phẳng tọa độ $Oxy$ cho hai đường thẳng song song $a$ và $a'$ lần lượt có phương trình \(3x - 4y + 5 = 0\) và \(3x - 4y = 0\). Phép tịnh tiến theo \(\overrightarrow u \) biến đường thẳng $a$ thành đường thẳng $a'$. Khi đó độ dài bé nhất của vectơ \(\overrightarrow u \) bằng bao nhiêu?
-
A.
\(5\)
-
B.
\(4\)
-
C.
\(\sqrt 2 \)
-
D.
\(1\)
Cho tứ diện $ABCD.$ Gọi $M, N, P, Q$ lần lượt là trung điểm của các cạnh $AB, AD, CD, BC.$ Mệnh đề nào sau đây là sai ?
-
A.
$MP, NQ $ chéo nhau
-
B.
$MN // PQ$ và $MN = PQ$
-
C.
$MNPQ $ là hình bình hành
-
D.
$MN // BD$ và \(MN = \dfrac{1}{2}BD\).
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
-
A.
\(CD,{\rm{ }}EF,{\rm{ }}EG.\)
-
B.
\(CD,{\rm{ }}IG,{\rm{ }}HF.\)
-
C.
\(AB,{\rm{ }}IG,{\rm{ }}HF\).
-
D.
\(AC,{\rm{ }}IG,{\rm{ }}BD.\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Xét các khẳng định sau:
(1) MN // (SCD) (2) EF // (SAD)
(3) NE // (SAC) (3) IJ // (SAB)
Có bao nhiêu khẳng định đúng?
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Cho tứ diện $ABCD. $ Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác $BCD$ và $ACD.$ Chọn câu sai ?
-
A.
\({G_1}{G_2}// (ABD)\)
-
B.
\({G_1}{G_2}// (ABC)\)
-
C.
\(B{G_1};A{G_2};CD\) đồng quy
-
D.
\({G_1}{G_2} = \dfrac{2}{3}AB\)
Cho hình hộp $ABCD.A'B'C'D'$. Mặt phẳng $\left( {AB'D'} \right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?
-
A.
\(\left( {BCA'} \right)\)
-
B.
\(\left( {BC'D} \right)\)
-
C.
\(\left( {A'C'C} \right)\)
-
D.
\(\left( {BDA'} \right)\)
Cho hình bình hành \(ABCD\). Vẽ các tia \(Ax,By,Cz,Dt\) song song, cùng hướng nhau và không nằm trong \(mp\left( {ABCD} \right)\). Mặt phẳng \(\left( \alpha \right)\) cắt \(Ax,By,Cz,Dt\) lần lượt tại \(A',B',C',D'\), gọi \(O,O'\) lần lượt là tâm hình bình hành và giao điểm của hai đường thẳng \(A'C'\) với \(B'D'\). Khẳng định nào sau đây sai?
-
A.
\(A'B'C'D'\) là hình bình hành
-
B.
\(mp\left( {AA'B'B} \right)//mp\left( {DD'C'C} \right)\)
-
C.
\(AA' = CC'\) và \(BB' = DD'\)
-
D.
\(OO'//AA'\)
Cho hình chóp $S.ABC$ có $\widehat {BSC} = {120^0},\widehat {CSA} = {60^0},\widehat {ASB} = {90^0},$ $SA = SB = SC.$ Gọi $I$ là hình chiếu vuông góc của $S$ lên $mp\left( {ABC} \right).$ Chọn khẳng định đúng trong các khẳng định sau
-
A.
\(I\) là trung điểm $AB$.
-
B.
\(I\) là trọng tâm tam giác $ABC$.
-
C.
\(I\) là trung điểm $AC$.
-
D.
\(I\) là trung điểm $BC$.
Trong các mệnh đề sau mệnh đề nào đúng?
-
A.
Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho
-
B.
Nếu \(a\) và \(b\) song song (hoặc \(a\) trùng với \(b\)) thì góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(b\) và mặt phẳng \(\left( P \right)\) .
-
C.
Nếu góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\) thì mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\).
-
D.
Góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(b\) và mặt phẳng \(\left( P \right)\) thì \(a\) song song với \(b\).
Cho hình thoi $ABCD$ có tâm $O,\widehat {ADC} = {60^0},AC = 2a$. Lấy điểm $S$ không thuộc $\left( {ABCD} \right)$ sao cho $SO \bot \left( {ABCD} \right)$. Gọi \(\alpha \) là góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABCD} \right)\) và \(\tan \alpha = \dfrac{1}{2}\). Gọi \(\beta \) là góc giữa $SC$ và $\left( {ABCD} \right)$, chọn mệnh đề đúng :
-
A.
$\sin \beta = \dfrac{1}{2}$.
-
B.
$\cot \beta = \dfrac{{\sqrt 3 }}{2}$.
-
C.
$\tan \beta = \dfrac{{\sqrt 3 }}{2}$.
-
D.
$\beta = {60^0}$.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = a,{\rm{ }}AC = a\sqrt 3 $. Tam giác $SBC$ đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $\left( {SAC} \right)$.
-
A.
$d = \dfrac{{a\sqrt {39} }}{{13}}.$
-
B.
$d = a.$
-
C.
$d = \dfrac{{2a\sqrt {39} }}{{13}}.$
-
D.
$d = \dfrac{{a\sqrt 3 }}{2}.$
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.
-
A.
$1.$
-
B.
$\sqrt 2 .$
-
C.
$2.$
-
D.
$4.$
Cho hàm số \(y = {x^3} - 3m{x^2} + 4{m^2} - 2\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có hai điểm cực trị \(A,{\rm{ }}B\) sao cho \(I\left( {1;0} \right)\) là trung điểm của đoạn thẳng \(AB\).
-
A.
\(m = 0\)
-
B.
\(m = - 1\)
-
C.
\(m = 1\)
-
D.
\(m = 2.\)
Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:
-
A.
$m \ge 12$
-
B.
$m \le 12$
-
C.
$m \ge 0$
-
D.
$m \le 0$
Tính đạo hàm của hàm số \(y = \dfrac{1}{{{x^2} - 2x + 5}}.\)
-
A.
$y' = \dfrac{{2x - 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}.$
-
B.
$y' = \dfrac{{ - 2x + 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}.$
-
C.
\(y' = (2x - 2)({x^2} - 2x + 5).\)
-
D.
\(y' = \dfrac{1}{{2x - 2}}.\)
Cho hàm số \(y = \dfrac{x}{{\sqrt {4 - {x^2}} }}.\) Khi đó \(y'\left( 0 \right)\) bằng:
-
A.
\(y'\left( 0 \right) = \dfrac{1}{2}\).
-
B.
\(y'\left( 0 \right) = \dfrac{1}{3}\).
-
C.
\(y'\left( 0 \right) = 1\).
-
D.
\(y'\left( 0 \right) = 2\).
Chọn đáp án đúng:
-
A.
\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
-
B.
\(\mathop {\lim }\limits_{x \to {x_0}} x = 1\)
-
C.
\(\mathop {\lim }\limits_{x \to {x_0}} c = {x_0}\)
-
D.
\(\mathop {\lim }\limits_{x \to {x_0}} x = 0\)
Giá trị của giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[3]{{3{x^3} - 1}} + \sqrt {{x^2} + 2} } \right)\) là:
-
A.
\(\sqrt[3]{3} + 1.\)
-
B.
\( + \infty .\)
-
C.
\(\sqrt[3]{3} - 1.\)
-
D.
\( - \infty \).
Biết rằng \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1.\) Tìm giá trị thực của tham số \(m\) để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}}}&{{\rm{khi }}x \ne \pi }\\m&{{\rm{khi }}x = \pi }\end{array}} \right.$ liên tục tại \(x = \pi .\)
-
A.
\(m = \dfrac{\pi }{2}.\)
-
B.
\(m = - \dfrac{\pi }{2}.\)
-
C.
\(m = \dfrac{1}{2}.\)
-
D.
\(m = - \dfrac{1}{2}.\)
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân ở \(C\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AB\) và \(SB\). Biết \(HK \bot \left( {ABC} \right)\), khẳng định nào sau đây sai?
-
A.
\(CH \bot HK\).
-
B.
\(AB \bot \left( {CHK} \right)\).
-
C.
\(CH \bot AK\).
-
D.
\(BC \bot \left( {SAC} \right)\).
Cho chóp đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 3. Gọi \(\varphi \) là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?
-
A.
\(\tan \varphi = \sqrt 7 \)
-
B.
\(\varphi = {60^0}\)
-
C.
\(\varphi = {45^0}\)
-
D.
\(\tan \varphi = \dfrac{{\sqrt {14} }}{2}\)
Tìm tập xác định của hàm số sau \(y = \tan \left( {2x + \dfrac{\pi }{3}} \right)\).
-
A.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{4} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{{12}} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{8} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
Số điện thoại ở Huyện Củ Chi có $7$ chữ số và bắt đầu bởi $3$ chữ số đầu tiên là $790$. Hỏi ở Huyện Củ Chi có tối đa bao nhiêu máy điện thoại:
-
A.
$1000$.
-
B.
$100000$.
-
C.
$10000$.
-
D.
$1000000$.
Nghiệm của phương trình: \(\sin 2x - \sqrt 3 \sin x = 0\) là:
-
A.
\(\left[ \begin{array}{l}x = k\pi \\x = \pm \dfrac{\pi }{6} + k2\pi \end{array} \right.\).
-
B.
\(\left[ \begin{array}{l}x = k\pi \\x = \pm \dfrac{\pi }{6} + k\pi \end{array} \right.\).
-
C.
\(\left[ \begin{array}{l}x = k2\pi \\x = \pm \dfrac{\pi }{3} + k2\pi \end{array} \right.\).
-
D.
\(x = \pm \dfrac{\pi }{6} + k2\pi \).
Số các hoán vị của \(17\) phần tử là:
-
A.
\({17^2}\)
-
B.
\(17!\)
-
C.
\(17.16\)
-
D.
\(17\)
Đội thanh niên xung kích của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp \(A\), 4 học sinh lớp \(B\) và 3 học sinh lớp \(C\). Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong 3 lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
-
A.
\(120.\)
-
B.
\(90.\)
-
C.
\(270.\)
-
D.
\(225.\)
Tính tổng \(S = C_{100}^0 - 5C_{100}^1 + {5^2}C_{100}^2 - ... + {5^{100}}C_{100}^{100}\)
-
A.
\({6^{100}}\).
-
B.
\({4^{100}}\).
-
C.
\({2^{300}}\).
-
D.
\({3^{200}}\).
Một lô hàng gồm $1000$ sản phẩm, trong đó có $50$ phế phẩm. Lấy ngẫu nhiên từ lô hàng đó $1$ sản phẩm. Xác suất để lấy được sản phẩm tốt là:
-
A.
$0,94.$
-
B.
$0,96.$
-
C.
$0,95.$
-
D.
$0,97.$
Một con xúc sắc cân đối và đồng chất được gieo ba lần. Gọi $P$ là xác suất để tổng số chấm xuất hiện ở hai lần gieo đầu bằng số chấm xuất hiện ở lần gieo thứ ba. Khi đó $P$ bằng:
-
A.
$\dfrac{{10}}{{216}}$.
-
B.
$\dfrac{{15}}{{216}}$.
-
C.
$\dfrac{{16}}{{216}}$.
-
D.
$\dfrac{{12}}{{216}}$.
Cho dãy số $\dfrac{1}{2};0; - \dfrac{1}{2}; - 1; - \dfrac{3}{2}$ là cấp số cộng với:
-
A.
Số hạng đầu tiên là $\dfrac{1}{2}$, công sai là $\dfrac{1}{2}.$
-
B.
Số hạng đầu tiên là $\dfrac{1}{2}$, công sai là $ - \dfrac{1}{2}.$
-
C.
Số hạng đầu tiên là $0$, công sai là $\dfrac{1}{2}.$
-
D.
Số hạng đầu tiên là $0$, công sai là $ - \dfrac{1}{2}.$
Cho cấp số cộng \(\left( {{u_n}} \right)\). Mệnh đề nào dưới đây là mệnh đề đúng
-
A.
\(\left( {n - p} \right){u_m} + \left( {p - m} \right){u_n} + \left( {m - n} \right){u_p} = 0\).
-
B.
\(\left( {m - n} \right){u_m} + \left( {n - p} \right){u_n} + \left( {p - m} \right){u_p} = 0\).
-
C.
\(\left( {m - p} \right){u_m} + \left( {n - m} \right){u_n} + \left( {p - n} \right){u_p} = 0\).
-
D.
\(\left( {p - n} \right){u_m} + \left( {m - p} \right){u_n} + \left( {m - n} \right){u_p} = 0\).
Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là:
-
A.
$720$
-
B.
$81$
-
C.
$64$
-
D.
$56$
Có bao nhiêu số nguyên \(m \in \left[ { - 5;5} \right]\) để \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\).
-
A.
$6$
-
B.
$4$
-
C.
$3$
-
D.
$5$
Cho phương trình \(\left( {2\sin x - 1} \right)\left( {\sqrt 3 \tan x + 2\sin x} \right) = 3 - 4{\cos ^2}x\). Tổng tất cả các nghiệm thuộc đoạn \(\left[ {0;\,20\pi } \right]\) của phương trình bằng
-
A.
\(\dfrac{{1150}}{3}\pi \).
-
B.
\(\dfrac{{570}}{3}\pi \).
-
C.
\(\dfrac{{880}}{3}\pi \).
-
D.
\(\dfrac{{875}}{3}\pi \).
Cho tứ diện \(ABCD\) có \(AB = CD = 4,BC = AD = 5,AC = BD = 6\). \(M\) là điểm thay đổi trong tâm giác \(ABC\). Các đường thẳng qua \(M\) song song với \(AD,BD,CD\) tương ứng cắt mặt phẳng \(\left( {BCD} \right),\left( {ACD} \right),\left( {ABD} \right)\) tại \(A',B',C'\). Giá trị lớn nhất của \(MA'.MB'.MC'\) là
-
A.
\(\dfrac{{40}}{9}\)
-
B.
\(\dfrac{{24}}{9}\)
-
C.
\(\dfrac{{30}}{9}\)
-
D.
\(\dfrac{{20}}{9}\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Lời giải và đáp án
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
-
A.
${x_0}$ là điểm cực đại của hàm số.
-
B.
${x_0}$ là điểm cực tiểu của hàm số.
-
C.
${x_0}$ là điểm cực đại của đồ thị hàm số.
-
D.
${x_0}$ là điểm cực tiểu của đồ thị hàm số.
Đáp án : B
Nếu $\left\{ \begin{gathered}f'\left( x \right) < 0,\forall x \in \left( {{x_0} - h} \right) \hfill \\f'\left( x \right) > 0,\forall x \in \left( {{x_0} + h} \right) \hfill \\ \end{gathered} \right.$ thì ${x_0}$ là một điểm cực tiểu của hàm số.
Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thì ${x_0}$ là điểm cực tiểu của hàm số.
Một số em có thể chọn nhầm đáp án D vì không phân biệt được khái niệm điểm cực tiểu của hàm số và điểm cực tiểu của đồ thị hàm số.
Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ có cực đại và cực tiểu.
-
A.
$0 < m \leqslant 1.$
-
B.
$\left[ \begin{gathered}m < 0 \hfill \\m > 1 \hfill \\ \end{gathered} \right.$
-
C.
$0 < m < 1.$
-
D.
$m < 0.$
Đáp án : B
- Bước 1: Tính $y'$.
- Bước 2: Hàm số có cực đại và cực tiểu $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt $ \Leftrightarrow \Delta > 0$.
- Bước 3: Kết luận.
TXĐ: $D = R$
TH1: $m = 0 \to y = x - 1.$
Hàm số không có cực trị.
TH2: $m \ne 0$.
Ta có: $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ $ \Rightarrow y' = m{x^2} - 2mx + 1.$
Để hàm số cho có cực đại, cực tiểu thì phương trình $y' = 0$ phải có $2$ nghiệm phân biệt
$ \Rightarrow \Delta ' = {m^2} - m > 0 \Leftrightarrow \left[ \begin{gathered} m < 0 \hfill \\ m > 1 \hfill \\\end{gathered} \right..$
Học sinh cần nhớ xét trường hợp $m=0$ khi hệ số trước $x$ có mũ cao nhất chứa tham số.
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
-
A.
$f\left( 0 \right) < 5$
-
B.
$f\left( 2 \right) \geqslant 5$
-
C.
$f\left( 1 \right) = 5$
-
D.
$f\left( 0 \right) = 5$
Đáp án : B
GTNN của $f\left( x \right)$ trên $\left[ {0;2} \right]$ bằng $5$ nên $f\left( x \right) \geqslant 5,\forall x \in \left[ {0;2} \right] \Rightarrow f\left( 2 \right) \geqslant 5$.
Gieo đồng xu hai lần liên tiếp. Biến cố \(A\) là biến cố “Mặt ngửa xuất hiện đúng 1 lần”. Số phần tử của \({\Omega _A}\) là:
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(3\)
-
D.
\(4\)
Đáp án : A
Liệt kê và đếm số phần tử của \({\Omega _A}\).
Ta có: \({\Omega _A} = \left\{ {NS,SN} \right\}\).
Một số em có thể sẽ chọn nhầm đáp án B vì coi hai trường hợp \(SN\) và \(NS\) cùng là một là sai. Cần lưu ý rằng gieo con xúc sắc hai lần nên \(SN,NS\) là hai giá trị khác nhau.
Số đo bốn góc của một tứ giác lồi lập thành một cấp số nhân, biết rằng số đo của góc lớn nhất gấp $8$ lần số đo của góc nhỏ nhất. Tìm góc lớn nhất:
-
A.
${190^0}$
-
B.
${191^0}$
-
C.
${192^0}$
-
D.
${193^0}$
Đáp án : C
Gọi số đo góc nhỏ nhất là \(A\) và biểu diễn các góc còn lại theo \(A\), sử dụng đinh nghĩa cấp số nhân.
Gọi $A,B,C,D$ là số đo của bốn góc của tứ giác lồi đã cho. Không mất tính tổng quát, giả sử \(A < B < C < D\).
Theo giả thiết ta có $D = 8A$ và $A,B,C,D$ theo thứ tự đó lập thành cấp số nhân. Gọi $q$ là công bội của cấp số nhân đó, ta có:
\(\begin{array}{l}8A = D = A.{q^3} \Leftrightarrow q = 2 \\ \Rightarrow {360^0} = A + B + C + D \\ = A + 2A + 4A + 8A = 15A\\ \Rightarrow A = 24{}^0 \Rightarrow D = 24{}^0.8 = {192^0}\end{array}\)
Các em cũng có thể sử dụng công thức tổng cấp số nhân như sau:
Áp dụng công thức \(S = \frac{{{u_1}\left( {{q^n} - 1} \right)}}{{q - 1}}\) ta có:
\(360 = \frac{{A\left( {{2^4} - 1} \right)}}{{2 - 1}} \Leftrightarrow 15A = 360\) \( \Leftrightarrow A = 24 \Rightarrow D = {24.2^3} = 192\)
Từ các chữ số $1,2,3,4,5,6,7$ lập được bao nhiêu số tự nhiên gồm $4$ chữ số khác nhau và là số chẵn?
-
A.
$360$
-
B.
$343$
-
C.
$523$
-
D.
$347$
Đáp án : A
Sử dụng quy tắc nhân với chú ý có bốn công đoạn để lập được số thỏa mãn bài toán.
Gọi số tự nhiên có $4$ chữ số cần tìm là \(\overline {abcd} \,\,\left( {a \ne 0,a \ne b \ne c \ne d} \right)\), \(d \in \left\{ {2;4;6} \right\}\)
Vì \(\overline {abcd} \) là số chẵn nên \(d \in \left\{ {2;4;6} \right\} \)
\(\Rightarrow \) Có $3$ cách chọn $d.$
Vì $a \ne d$ nên có $6$ cách chọn $a$
$b\ne a, d$ nên có $5$ cách chọn $b$
$c \ne a, b, d$ nên có $4$ cách chọn $c$
Áp dụng quy tắc nhân ta có số các số thỏa mãn là: $3.6.5.4 = 360$ (số)
Đối với bài toán này, vì số cần lập là số chẵn nên ta ưu tiên chọn $d$ trước rồi mới đến các chữ số khác.
Giá trị của biểu thức \(S = {9^{99}}C_{99}^0 + {9^{98}}C_{99}^1 + {9^{97}}C_{99}^2 + ... + 9C_{99}^{98} + C_{99}^{99}\)\(\) bằng:
-
A.
\({10^{98}}\)
-
B.
\({10^{100}}\)
-
C.
\({10^{99}}\)
-
D.
Đáp án khác
Đáp án : C
+) Xuất phát từ khai triển nhị thức \({\left( {a + b} \right)^n} = C_n^0{a^n} + C_n^1{a^{n - 1}}b + C_n^2{a^{n - 2}}{b^2} + ... + C_n^{n - 1}a{b^{n - 1}} + C_n^n{b^n}\)
+) Thay \(a,b,n\) bằng các giá trị thích hợp.
Ta có: \({\left( {a + b} \right)^{99}} = C_{99}^0{a^{99}} + C_{99}^1{a^{98}}b + C_{99}^2{a^{97}}{b^2} + ... + C_{99}^{98}a{b^{98}} + C_{99}^{99}{b^{99}}\)
Thay \(a = 9,b = 1\) ta có:
\(\begin{array}{l}{\left( {9 + 1} \right)^{99}} = C_{99}^0{.9^{99}} + C_{99}^1{.9^{98}}.1 + C_{99}^2{.9^{97}}{.1^2} + ... + C_{99}^{98}{.9.1^{98}} + C_{99}^{99}{.1^{99}}\\ \Leftrightarrow {10^{99}} = {9^{99}}C_{99}^0 + {9^{98}}C_{99}^1 + {9^{97}}C_{99}^2 + ... + 9C_{99}^{98} + C_{99}^{99}\end{array}\)
Nghiệm của phương trình \({\sin ^2}x-\sin x = 0\) thỏa điều kiện: \(0 < x < \pi \).
-
A.
\(x = \dfrac{\pi }{2}\).
-
B.
\(x = \pi \).
-
C.
\(x = 0\).
-
D.
\(x = - \dfrac{\pi }{2}\).
Đáp án : A
Bước 1: Đưa phương trình về dạng tích
Bước 2: Giải từng phương trình
Áp dụng công thức: $\sin x=0 \Leftrightarrow x=k\pi$ và $\cos x=0 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi $, $k\in \mathbb{Z}$
Bước 3: Xét từng họ nghiệm và giải bất phương trình nghiệm nguyên ẩn k rồi kết luận.
Bước 1:
\({\sin ^2}x-\sin x = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\sin x = 1\end{array} \right.\)
Bước 2:
\( \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Bước 3:
Xét $x = k\pi,k \in \mathbb{Z}$:
Vì \(0 < x < \pi \) nên nghiệm của phương trình thỏa mãn:
\(0 < k\pi < \pi \Leftrightarrow 0<k<1\)
Ta không thể tìm được số nguyên nào thỏa mãn điều trên
=> Không có số $k$ trong trường hợp này.
Xét $x = \dfrac{\pi }{2} + k2\pi,k \in \mathbb{Z}$:
Vì \(0 < x < \pi \) nên nghiệm của phương trình thỏa mãn:
\(0 <\dfrac{\pi }{2} + k2\pi<\pi \Leftrightarrow -\dfrac{\pi }{2} <k2\pi<\dfrac{\pi }{2} \)
\( \Leftrightarrow - \dfrac{1}{4} < k < \dfrac{1}{4}\) mà \(k \in \mathbb{Z} \Rightarrow k = 0\). Thay vào x ta được:
\(x = \dfrac{\pi }{2} + 0 = \dfrac{\pi }{2}\)
Vậy phương trình có 1 nghiệm duy nhất là \(x= \dfrac{\pi }{2}\)
Một số em có thể sẽ chọn nhầm đáp án B vì giải sai phương trình dẫn đến tìm ra hai nghiệm \(0\) và \(\dfrac{\pi }{3}\) là sai.
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}}\,\,khi\,\,x \ne 3\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 3\end{array} \right.\). Tìm tất cả các giá trị của tham số thực $m$ để hàm số liên tục tại $x = 3.$
-
A.
\(m \in \emptyset \)
-
B.
\(m \in R\)
-
C.
$m = 1$
-
D.
\(m = - 1\)
Đáp án : A
Xét tính liên tục của hàm số tại $x = 3.$
Để hàm số liên tục tại $x = 3$ thì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)\)
Hàm số đã cho xác định trên R.
Ta có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\left| {x - 3} \right|}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{ - \left( {x - 3} \right)}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( { - 1} \right) = - 1\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\left| {x - 3} \right|}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{x - 3}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \left( 1 \right) = 1\end{array}\)
Vậy $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) \Rightarrow $ Không tồn tại $\mathop {\lim }\limits_{x \to 3} f\left( x \right)$.
Vậy không có giá trị nào của $m$ để hàm số liên tục tại $x = 3.$
Các em học sinh thường sai lầm khi không tính giới hạn trái và giới hạn phải trong bài toán trên. Nhiều học sinh có lời giải sai như sau :
$\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \dfrac{{x - 3}}{{x - 3}} = 1 \Rightarrow $ Hàm số liên tục tại $x = 3$ \( \Leftrightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) \Leftrightarrow m = 1\) và chọn nhầm đáp án sai.
Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y = {x^4} + 2{x^2} - 1$ trên đoạn $\left[ { - 1;2} \right]$ lần lượt là $M$ và $m$. Khi đó giá trị của $M.m$ là:
-
A.
$ - 2$
-
B.
$46$
-
C.
$ - 23$
-
D.
$23$
Đáp án : C
Phương pháp tìm GTLN, GTNN của hàm số $y = f\left( x \right)$ trên $\left[ {a;b} \right]$:
- Tính $y'$, tìm các nghiệm ${x_1},{x_2},...,{x_n}$của phương trình $y' = 0$ mà $a \leqslant {x_1} < {x_2} < ... < {x_n} \leqslant b$ .
- Tính các giá trị $f\left( a \right),f\left( {{x_1}} \right),...,f\left( {{x_n}} \right),f\left( b \right)$.
- So sánh các giá trị trên và kết luận.
TXĐ: $D=R$
Ta có: $y' = 4{{\text{x}}^3} + 4{\text{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0 \in \left[ { - 1;2} \right]$
$f( - 1) = 2,{\text{ f(0) = }} - 1,{\text{ f(2) = 23}}$
Ta thấy GTLN và GTNN lần lượt là $M = 23,m = - 1 \Rightarrow M.m = 23.\left( { - 1} \right) = - 23$
Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = \left( {x -1}\right)\left({{x^2}- 2} \right)\left( {{x^4} - 4} \right)$. Số điểm cực trị của hàm số $y = f\left( x \right)$ là:
-
A.
$3$
-
B.
$2$
-
C.
$4$
-
D.
$1$
Đáp án : D
- Bước 1: Giải phương trình $f'\left( x \right) = 0$.
- Bước 2: Xét dấu đạo hàm và kết luận.
+ Các điểm mà đạo hàm đổi dấu từ âm sang dương là các điểm cực tiểu.
+ Các điểm mà đạo hàm đổi dấu từ dương sang âm là các điểm cực đại.
Ta có: $f'\left( x \right) = 0$
$\begin{gathered} \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2}\right)\left( {{x^4} - 4} \right) = 0 \hfill \\\Leftrightarrow \left( {x - 1} \right){\left( {{x^2} - 2}\right)^2}\left( {{x^2} + 2} \right) = 0 \hfill \\ \Leftrightarrow \left[ \begin{gathered}x = 1 \hfill \\ x = \sqrt 2 \hfill \\x = - \sqrt { 2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $
Một điểm được gọi là cực trị của hàm số khi đạo hàm của hàm số đổi dấu qua điểm đó.
Ta nhận thấy đạo hàm của hàm số chỉ đổi dấu qua $x = 1$ và không đổi dấu qua $x = \pm \sqrt 2 $.
Vậy hàm số có $1$ điểm cực trị.
HS thường quên điều kiện đổi dấu của đạo hàm dẫn đến chọn nhầm đáp án A khi thấy phương trình $f'\left(x\right) = 0$ có 3 nghiệm.
Nghiệm của phương trình \(\sin 3x = \cos x\) là:
-
A.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2},x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
-
B.
\(x = k2\pi ,x = \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
C.
\(x = k\pi ,x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
-
D.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2},x = - \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
Đáp án : A
- Biến đổi phương trình về dạng \(\sin x = \sin y\) hoặc \(\cos x = \cos y\)
Sử dụng công thức: $\sin \left( {\dfrac{\pi }{2} - x} \right)=\cos x$
- Giải phương trình lượng giác cơ bản:
\(\sin x = \sin y \Leftrightarrow \left[ \begin{array}{l}x = y + k2\pi \\x = \pi - y + k2\pi \end{array} \right.\)
Ta có:
\(\sin 3x = \cos x \Leftrightarrow \sin 3x = \sin \left( {\dfrac{\pi }{2} - x} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}3x =\left( { \dfrac{\pi }{2} - x } \right)+ k2\pi \\3x = \pi - \left( {\dfrac{\pi }{2} - x } \right)+ k2\pi \end{array} \right. \)
\( \Leftrightarrow \left[ \begin{array}{l}4x = \dfrac{\pi }{2} + k2\pi \\2x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2}\\x = \dfrac{\pi }{4} + k\pi \end{array} \right.\left( {k \in Z} \right)\)
Một số em có thể sẽ nhớ nhầm công thức \(\cos x = \sin \left( {x - \dfrac{\pi }{2}} \right)\) dẫn đến chọn nhầm đáp án D là sai.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên trên khoảng $\left( {0;2} \right)$ như sau:

Khẳng định nào sau đây là khẳng định đúng:
-
A.
Trên $\left( {0;2} \right)$, hàm số không có cực trị
-
B.
Hàm số đạt cực đại tại $x = 1$
-
C.
Hàm số đạt cực tiểu tại $x = 1$
-
D.
Hàm số đạt cực tiểu tại $x = 0$
Đáp án : B
Quan sát bảng biến thiên và rút ra nhận xét dựa trên các khái niệm cực đại, cực tiểu.
A sai vì trên đoạn $\left( {0;2} \right)$ vẫn có cực trị tại $x = 1$.
Hàm số đạt cực đại tại $x=1$ nên B đúng.
C sai vì hàm số đạt cực đại tại $x = 1$ không phải cực tiểu
D sai vì đạo hàm không đổi dấu qua $x = 0$
Nhiều HS nhầm lẫn rằng hàm số không có đạo hàm tại $x = 1$ nên kết luận hàm số không có cực trị và chọn ngay đáp án A.
Điều này là sai vì vẫn có những điểm mà hàm số đạt cực trị nhưng không có đạo hàm tại điểm đó.
Chẳng hạn hàm số $y = \left| x \right|$ không có đạo hàm tại $x = 0$ nhưng $x = 0$ vẫn là điểm cực tiểu của hàm số.
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y = \sqrt {2\sin x + 3} \)
-
A.
\(\max y = \sqrt 5 ,\min y = 1\)
-
B.
\(\max y = \sqrt 5 ,\min y = 0\)
-
C.
\(\max y = \sqrt 5 ,\min y = \sqrt 3 \)
-
D.
\(\max y = \sqrt 5 ,\min y = 3\)
Đáp án : A
Sử dụng \( - 1 \le \sin x \le 1\) để đánh giá biểu thức \(\sqrt {2\sin x + 3} \), từ đó tìm được GTNN, GTLN của hàm số.
Do \( - 1 \le \sin x \le 1 \Rightarrow -2 \le 2\sin x \le 2 \)\(\Rightarrow -2+3 \le2\sin x + 3 \le 2+3 \)\(\Rightarrow1 \le \sqrt {2\sin x + 3} \le \sqrt 5 \).
Dấu “=” xảy ra khi lần lượt \(\sin x = - 1\) và $\sin x = 1$
Một số em có thể sẽ đánh giá \(\sqrt {2\sin x + 3} \ge 0,\forall x\) nên chọn nhầm đáp án B là sai.
Trong mặt phẳng tọa độ $Oxy$ cho hai đường thẳng song song $a$ và $a'$ lần lượt có phương trình \(3x - 4y + 5 = 0\) và \(3x - 4y = 0\). Phép tịnh tiến theo \(\overrightarrow u \) biến đường thẳng $a$ thành đường thẳng $a'$. Khi đó độ dài bé nhất của vectơ \(\overrightarrow u \) bằng bao nhiêu?
-
A.
\(5\)
-
B.
\(4\)
-
C.
\(\sqrt 2 \)
-
D.
\(1\)
Đáp án : D
- Độ dài bé nhất của vectơ \(\overrightarrow u \) bằng khoảng cách giữa hai đường thẳng $a$ và $a'$.
Lấy điểm $M\left( {0;0} \right)$ thuộc $a'$. Ta có: $d\left( {a;a'} \right) = d\left( {M;a} \right)$
\(d(M;a) = \dfrac{{\left| {3.0 - 4.0 + 5} \right|}}{{\sqrt {{3^2} + {{( - 4)}^2}} }} = 1\)
Cho tứ diện $ABCD.$ Gọi $M, N, P, Q$ lần lượt là trung điểm của các cạnh $AB, AD, CD, BC.$ Mệnh đề nào sau đây là sai ?
-
A.
$MP, NQ $ chéo nhau
-
B.
$MN // PQ$ và $MN = PQ$
-
C.
$MNPQ $ là hình bình hành
-
D.
$MN // BD$ và \(MN = \dfrac{1}{2}BD\).
Đáp án : A
- Đưa về cùng mặt phẳng.
- Sử dụng các tính chất đường trung bình của tam giác.
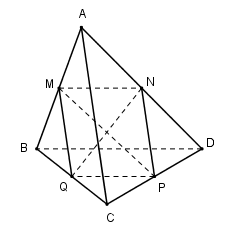
Ta có: $MN, PQ$ lần lượt là đường trung bình của tam giác $ABD$ và $CBD$ nên
$MN // BD ;$ \(MN = \dfrac{1}{2}BD\) và $ PQ // BD ;$ \(PQ = \dfrac{1}{2}BD\)
\( \Rightarrow \) $MN // PQ$ và $MN = PQ$
Do đó $MNPQ $ là hình bình hành nên $MP,NQ$ cùng thuộc một mặt phẳng.
Vậy A sai.
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
-
A.
\(CD,{\rm{ }}EF,{\rm{ }}EG.\)
-
B.
\(CD,{\rm{ }}IG,{\rm{ }}HF.\)
-
C.
\(AB,{\rm{ }}IG,{\rm{ }}HF\).
-
D.
\(AC,{\rm{ }}IG,{\rm{ }}BD.\)
Đáp án : B
Để chứng minh ba đường thẳng \({d_1},{\rm{ }}{d_2},{\rm{ }}{d_3}\) đồng quy ta chứng minh giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\) là điểm chung của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\); đồng thời \({d_3}\) là giao tuyến \(\left( \alpha \right)\) và \(\left( \beta \right)\).
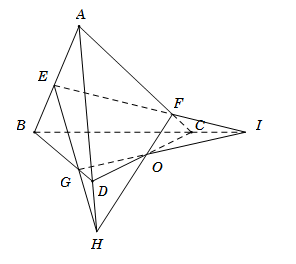
Trong $mp(EHI)$, gọi \(O = HF \cap IG\). Ta có
● \(O \in HF\) mà \(HF \subset \left( {ACD} \right)\) suy ra \(O \in \left( {ACD} \right)\).
● \(O \in IG\) mà \(IG \subset \left( {BCD} \right)\) suy ra \(O \in \left( {BCD} \right)\).
Do đó \(O \in \left( {ACD} \right) \cap \left( {BCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in CD\).
Vậy ba đường thẳng \(CD,{\rm{ }}IG,{\rm{ }}HF\) đồng quy.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Xét các khẳng định sau:
(1) MN // (SCD) (2) EF // (SAD)
(3) NE // (SAC) (3) IJ // (SAB)
Có bao nhiêu khẳng định đúng?
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : B
- Đưa về cùng mặt phẳng
- Chứng minh đường thẳng song song với mặt phẳng a // b \( \subset \left( P \right) \Rightarrow \)a // (P).
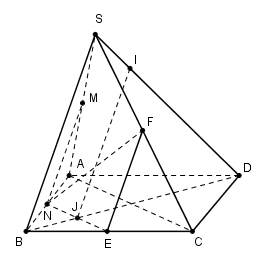
Trước hết ta lấy điểm \(M \in \left( P \right)\) sao cho \(M \in SA\).
Trong mp(SAB) kẻ MN // SA \(\left( {N \in AB} \right)\), trong mp(ABCD) kẻ NE // AC \(\left( {E \in BC} \right)\).
\(NE \cap BD = \left\{ J \right\}\)
Trong mp(SBC) kẻ EF // SB \(\left( {F \in SC} \right)\), trong mp(SBD) kẻ JI // SD \(\left( {I \in SD} \right)\).
Giả sử MN // (SCD)
Lại có: MN // SB\( \Rightarrow SB \subset \left( {SCD} \right)\) (vô lý) nên (1) sai.
Tương tự ta chứng minh được (2) sai.
NE // AC\( \subset \left( {SAC} \right) \Rightarrow \) NE // (SAC). Do đó (3) đúng.
IJ // SB\( \subset \left( {SAB} \right) \Rightarrow \)IJ // (SAB). Do đó (4) đúng.
Cho tứ diện $ABCD. $ Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác $BCD$ và $ACD.$ Chọn câu sai ?
-
A.
\({G_1}{G_2}// (ABD)\)
-
B.
\({G_1}{G_2}// (ABC)\)
-
C.
\(B{G_1};A{G_2};CD\) đồng quy
-
D.
\({G_1}{G_2} = \dfrac{2}{3}AB\)
Đáp án : D
- Sử dụng các tính chất của trọng tâm tam giác.
- Áp dụng định lí Ta-let đảo để suy ra các đường thẳng song song.
- Sử dụng định nghĩa đường thẳng song song với mặt phẳng.
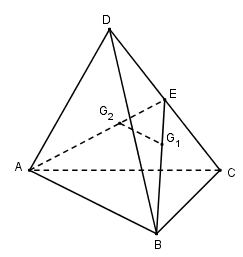
Gọi $E$ là trung điểm của $CD$\( \Rightarrow {G_1} \in BE;{G_2} \in AE \Rightarrow B{G_1};A{G_2};CD\) đồng quy tại $E.$ Suy ra C đúng.
Ta có: \(\dfrac{{E{G_1}}}{{EB}} = \dfrac{{E{G_2}}}{{EA}} = \dfrac{1}{3} \) \(\Rightarrow {G_1}{G_2}// AB\) và ${G_1}{G_2} = \dfrac{1}{3}AB$ (Định lí Ta-let đảo)
Mà \(AB \subset \left( {ABD} \right) \Rightarrow {G_1}{G_2}// (ABD)\)
\(AB \subset \left( {ABC} \right) \Rightarrow {G_1}{G_2}// (ABC).\)
Suy ra A và B đúng. Vậy D sai
Cho hình hộp $ABCD.A'B'C'D'$. Mặt phẳng $\left( {AB'D'} \right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?
-
A.
\(\left( {BCA'} \right)\)
-
B.
\(\left( {BC'D} \right)\)
-
C.
\(\left( {A'C'C} \right)\)
-
D.
\(\left( {BDA'} \right)\)
Đáp án : B
- Bước 1: Chứng minh mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng \(a,b\) cắt nhau lần lượt song song với hai đường thẳng \(a',b'\) cắt nhau trong mặt phẳng \(\left( \beta \right)\).
- Bước 2: Kết luận \(\left( \alpha \right)//\left( \beta \right)\).
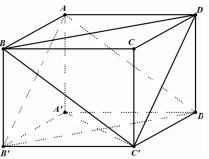
Do \(ADC'B'\) là hình bình hành nên \(AB'//DC'\).
Do \(ABC'D'\) là hình bình hành nên \(AD'//BC'\).
Mà \(AB',AD' \subset \left( {AB'D'} \right);BC',DC' \subset \left( {BC'D} \right)\) nên \(\left( {AB'D'} \right)//\left( {BC'D} \right)\).
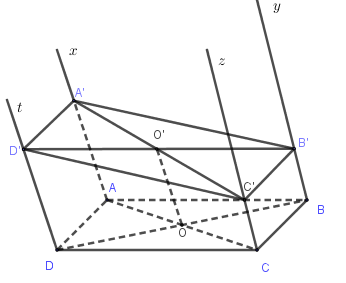
Cho hình bình hành \(ABCD\). Vẽ các tia \(Ax,By,Cz,Dt\) song song, cùng hướng nhau và không nằm trong \(mp\left( {ABCD} \right)\). Mặt phẳng \(\left( \alpha \right)\) cắt \(Ax,By,Cz,Dt\) lần lượt tại \(A',B',C',D'\), gọi \(O,O'\) lần lượt là tâm hình bình hành và giao điểm của hai đường thẳng \(A'C'\) với \(B'D'\). Khẳng định nào sau đây sai?
-
A.
\(A'B'C'D'\) là hình bình hành
-
B.
\(mp\left( {AA'B'B} \right)//mp\left( {DD'C'C} \right)\)
-
C.
\(AA' = CC'\) và \(BB' = DD'\)
-
D.
\(OO'//AA'\)
Đáp án : C
Xét tính đúng sai của các đáp án, sử dụng các phương pháp chứng minh hai mặt phẳng song song, hai đường thẳng song song.
Ta có: \(AB//CD,AA'//DD'\) và \(AA',AB \subset \left( {ABB'A'} \right);CD,DD' \subset \left( {CDD'C'} \right)\)
Do đó \(mp\left( {AA'B'B} \right)//mp\left( {DD'C'C} \right)\), đáp án B đúng.
Mặt khác,
\(\left. \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {ABB'A'} \right) = A'B'\\\left( {A'B'C'D'} \right) \cap \left( {DCC'D'} \right) = C'D'\\\left( {ABB'A'} \right)//\left( {DCC'D'} \right)\end{array} \right\} \Rightarrow A'B'//C'D'\)
\(\left. \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {ADD'A'} \right) = A'D'\\\left( {A'B'C'D'} \right) \cap \left( {BCC'B'} \right) = C'B'\\\left( {ADD'A'} \right)//\left( {BCC'B'} \right)\end{array} \right\} \Rightarrow A'D'//C'B'\)
Do đó, tứ giác \(A'B'C'D'\) là hình bình hành nên đáp án A đúng.
Do \(O,O'\) lần lượt là tâm các hình bình hành nên \(O,O'\) lần lượt là trung điểm của \(AC,A'C'\) nên \(OO'\) là đường trung bình trong hình thang \(AA'C'C\).
Do đó \(OO'//AA'\) nên D đúng.
Cho hình chóp $S.ABC$ có $\widehat {BSC} = {120^0},\widehat {CSA} = {60^0},\widehat {ASB} = {90^0},$ $SA = SB = SC.$ Gọi $I$ là hình chiếu vuông góc của $S$ lên $mp\left( {ABC} \right).$ Chọn khẳng định đúng trong các khẳng định sau
-
A.
\(I\) là trung điểm $AB$.
-
B.
\(I\) là trọng tâm tam giác $ABC$.
-
C.
\(I\) là trung điểm $AC$.
-
D.
\(I\) là trung điểm $BC$.
Đáp án : D
- Sử dụng định lý Pi-ta-go đảo và định lý hàm số cos để chứng minh \(\Delta ABC\) vuông tại \(A\).
- Sử dụng định nghĩa trục đường tròn đáy để tìm hình chiếu của \(S\) trên mặt đáy.
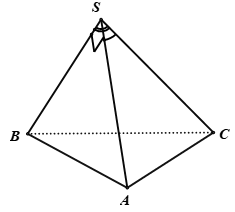
Gọi \(SA = SB = SC = a\)
Ta có :$\vartriangle SAC$ đều \( \Rightarrow AC = SA = a\)
$\vartriangle SAB$ vuông cân tại $S$ \( \Rightarrow AB = a\sqrt 2 \)
\(BC = \sqrt {S{B^2} + S{C^2} - 2SB.SC.\cos \widehat {BSC}} = a\sqrt 3 \)
$\vartriangle ABC$ vuông tại $A$
Gọi $I$ là trung điểm của $AC$ thì là tâm đường tròn
ngoại tiếp tam giác $ABC.$
Do \(SA = SB = SC\) và \(IA = IB = IC\) nên \(SI \bot \left( {ABC} \right)\).
Vậy \(I\) là hình chiếu vuông góc của $S$ lên mặt phẳng $\left( {ABC} \right)$
Trong các mệnh đề sau mệnh đề nào đúng?
-
A.
Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho
-
B.
Nếu \(a\) và \(b\) song song (hoặc \(a\) trùng với \(b\)) thì góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(b\) và mặt phẳng \(\left( P \right)\) .
-
C.
Nếu góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\) thì mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\).
-
D.
Góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(b\) và mặt phẳng \(\left( P \right)\) thì \(a\) song song với \(b\).
Đáp án : B
Sử dụng các định nghĩa, tính chất của góc giữa đường thẳng và mặt phẳng để xét tính đúng, sai cho từng đáp án.
Đáp án A sai vì nếu trường hợp đường thẳng vuông góc với mặt phẳng thì định nghĩa đó không còn đúng.
Đáp án C sai vì \(\left( P \right)\) và \(\left( Q \right)\) có thể trùng nhau.
Đáp án D sai vì \(a,b\) có thể trùng nhau.
Một số em có thể sẽ chọn nhầm đáp án A vì không nhỡ kĩ định nghĩa góc giữa đường thẳng và mặt phẳng
Cho hình thoi $ABCD$ có tâm $O,\widehat {ADC} = {60^0},AC = 2a$. Lấy điểm $S$ không thuộc $\left( {ABCD} \right)$ sao cho $SO \bot \left( {ABCD} \right)$. Gọi \(\alpha \) là góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABCD} \right)\) và \(\tan \alpha = \dfrac{1}{2}\). Gọi \(\beta \) là góc giữa $SC$ và $\left( {ABCD} \right)$, chọn mệnh đề đúng :
-
A.
$\sin \beta = \dfrac{1}{2}$.
-
B.
$\cot \beta = \dfrac{{\sqrt 3 }}{2}$.
-
C.
$\tan \beta = \dfrac{{\sqrt 3 }}{2}$.
-
D.
$\beta = {60^0}$.
Đáp án : C
- Xác định góc giữa \(SB\) và \(\left( {ABCD} \right)\), tính \(SO\).
- Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\) và tính tỉ số lượng giác của góc đó.

Vì \(SO \bot \left( {ABCD} \right)\) nên \(OB\) là hình chiếu của \(SB\) trên mặt phẳng đáy.
Do đó \(\alpha = \left( {SB,\left( {ABCD} \right)} \right) = \left( {SB,OB} \right) = \widehat {SBO}\) và \(\beta = \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,OC} \right) = \widehat {SCO}\).
Hình thoi \(ABCD\) có \(AC = 2a,\widehat {ADC} = {60^0} \Rightarrow \Delta ADC\) đều \( \Rightarrow AD = 2a\)
Tam giác \(AOD\) vuông tại \(O\) nên \(OD = \sqrt {A{D^2} - A{O^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \Rightarrow OB = a\sqrt 3 \).
Lại có \(\tan \alpha = \dfrac{1}{2} \Rightarrow \dfrac{{SO}}{{OB}} = \dfrac{1}{2} \Rightarrow SO = \dfrac{1}{2}OB = \dfrac{1}{2}.a\sqrt 3 = \dfrac{{a\sqrt 3 }}{2}\).
Vậy \(\tan \beta = \tan \widehat {SCO} = \dfrac{{SO}}{{OC}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{a} = \dfrac{{\sqrt 3 }}{2}\).
Một số em có thể sẽ chọn nhầm đáp án D sau khi tính được \(\tan \beta = \dfrac{{\sqrt 3 }}{2} \Rightarrow \beta = {60^0}\) là sai.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = a,{\rm{ }}AC = a\sqrt 3 $. Tam giác $SBC$ đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $\left( {SAC} \right)$.
-
A.
$d = \dfrac{{a\sqrt {39} }}{{13}}.$
-
B.
$d = a.$
-
C.
$d = \dfrac{{2a\sqrt {39} }}{{13}}.$
-
D.
$d = \dfrac{{a\sqrt 3 }}{2}.$
Đáp án : C
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng
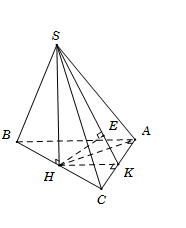
Gọi $H$ là trung điểm của $BC,$ suy ra $SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)$.
Gọi $K$ là trung điểm $AC$, suy ra $HK \bot AC$.
Kẻ $HE \bot SK\,\,\,\,\left( {E \in SK} \right).\,\,\,\,\,\,\,\,\left( 1 \right)$
Ta có:\(\left\{ \begin{array}{l}AC \bot HK\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot HE\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow HE \bot \left( {SAC} \right) \Rightarrow HE = d\left( {H;\left( {SAC} \right)} \right)\)
Ta có :
\(BH \cap \left( {SAC} \right) = C \Rightarrow \dfrac{{d\left( {B;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{BC}}{{HC}} = 2 \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right) = 2HE\)
Tam giác \(ABC\) vuông tại \(A\) nên \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + 3{a^2}} = 2a\)
Tam giác \(SBC\) đều cạnh \(2a\) nên đường cao \(SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)
Lại có \(HK\) là đường trung bình của tam giác \(ABC\) nên \(HK = \dfrac{1}{2}AB = \dfrac{a}{2}\)
Vậy \(d\left( {B;\left( {SAC} \right)} \right) = 2HE = \dfrac{{SH.HK}}{{\sqrt {S{H^2} + H{K^2}} }} = \dfrac{{2a\sqrt {39} }}{{13}}.\)
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.
-
A.
$1.$
-
B.
$\sqrt 2 .$
-
C.
$2.$
-
D.
$4.$
Đáp án : C
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng
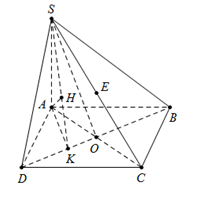
Ta có $E \in SC$, $EC \cap \left( {SBD} \right) = S \Rightarrow \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{ES}}{{CS}} = \dfrac{1}{2}$
Từ A kẻ $ AK \bot BD\left( {K \in BD} \right)$, kẻ $AH \bot SK\,\,\left( {H \in SK} \right)\,\,\,\,\,\,\left( 1 \right)$.
Ta có: \(\left\{ \begin{array}{l}BD \bot AK\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAK} \right) \Rightarrow BD \bot AH\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AH \bot \left( {SBD} \right).\)
$ \Rightarrow AH = d\left( {A;\left( {SBD} \right)} \right) = 2.d\left( {E;\left( {SBD} \right)} \right) = \dfrac{{2a}}{3}.$
Mà $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{K^2}}} \Rightarrow AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} - A{H^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$.
Tam giác $ABD$ vuông tại $A$, có đường cao $AK$.
$ \Rightarrow \dfrac{1}{{A{B^2}}} + \dfrac{1}{{AD{}^2}} = \dfrac{1}{{A{K^2}}} \Leftrightarrow \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}{x^2}}} = \dfrac{5}{{4{a^2}}} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{x^2} = 4\end{array} \right. \Rightarrow x = 2$
Cho hàm số \(y = {x^3} - 3m{x^2} + 4{m^2} - 2\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có hai điểm cực trị \(A,{\rm{ }}B\) sao cho \(I\left( {1;0} \right)\) là trung điểm của đoạn thẳng \(AB\).
-
A.
\(m = 0\)
-
B.
\(m = - 1\)
-
C.
\(m = 1\)
-
D.
\(m = 2.\)
Đáp án : C
- Tìm tọa độ hai điểm cực trị của đồ thị hàm số.
- Sử dụng công thức trung điểm tìm \(m\)
Ta có \(y' = 3{x^2} - 6mx = 3x\left( {x - 2m} \right);{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2m\end{array} \right..\)
Đề đồ thị hàm số có hai điểm cực trị \( \Leftrightarrow m \ne 0\).
Khi đó tọa độ hai điểm cực trị là \(A\left( {0;4{m^2} - 2} \right)\) và \(B\left( {2m;4{m^2} - 4{m^3} - 2} \right)\).
Do \(I\left( {1;0} \right)\) là trung điểm của \(AB\) nên \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_I}\\{y_A} + {y_B} = 2{y_I}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}0 + 2m = 2\\\left( {4{m^2} - 2} \right) + \left( {4{m^2} - 4{m^3} - 2} \right) = 0\end{array} \right. \Leftrightarrow m = 1:\) thỏa mãn.
Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:
-
A.
$m \ge 12$
-
B.
$m \le 12$
-
C.
$m \ge 0$
-
D.
$m \le 0$
Đáp án : A
Hàm số $y = a{x^3} + b{x^2} + cx + d,{\mkern 1mu} \left( {a \ne 0} \right)$ đồng biến trên $\left( {p;q} \right)$ khi và chỉ khi $y' \ge 0,{\mkern 1mu} \forall x \in \left( {p;q} \right)$.
Ta có $y' = 3{x^2} - 12x + m$. Để hàm số đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ thì $y' \ge 0{\mkern 1mu} ,\forall x > 0$
$ \Leftrightarrow 3{x^2} - 12x + m \ge 0,{\mkern 1mu} \forall x > 0 \Leftrightarrow - 3{x^2} + 12x \le m,\forall x > 0$. (*)
Xét $y = g\left( x \right) = - 3{x^2} + 12x$ với $x > 0$.
Ta có $g'\left( x \right) = - 6x + 12 = 0 \Leftrightarrow x = 2$(TM).
BBT $y = g\left( x \right)$ với $x > 0$.
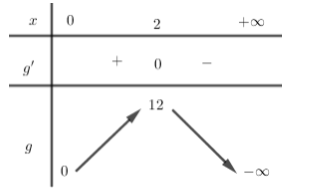
Từ BBT ta có $\mathop {\max }\limits_{\left( {0; + \infty {\rm{\;}}} \right)} {\mkern 1mu} g\left( x \right) = 12$, từ (*) suy ra $m \ge \mathop {\max }\limits_{\left( {0; + \infty {\rm{\;}}} \right)} {\mkern 1mu} g\left( x \right) = 12 \Leftrightarrow m \ge 12$.
Tính đạo hàm của hàm số \(y = \dfrac{1}{{{x^2} - 2x + 5}}.\)
-
A.
$y' = \dfrac{{2x - 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}.$
-
B.
$y' = \dfrac{{ - 2x + 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}.$
-
C.
\(y' = (2x - 2)({x^2} - 2x + 5).\)
-
D.
\(y' = \dfrac{1}{{2x - 2}}.\)
Đáp án : B
Sử dụng công thức tính đạo hàm \(\left( {\dfrac{1}{u}} \right)' = - \dfrac{{u'}}{{{u^2}}}\)
Ta có \(y' = \dfrac{{ - {{\left( {{x^2} - 2x + 5} \right)}^\prime }}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}} = \dfrac{{ - 2x + 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}\).
Cho hàm số \(y = \dfrac{x}{{\sqrt {4 - {x^2}} }}.\) Khi đó \(y'\left( 0 \right)\) bằng:
-
A.
\(y'\left( 0 \right) = \dfrac{1}{2}\).
-
B.
\(y'\left( 0 \right) = \dfrac{1}{3}\).
-
C.
\(y'\left( 0 \right) = 1\).
-
D.
\(y'\left( 0 \right) = 2\).
Đáp án : A
Sử dụng công thức đạo hàm của một thương \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\)
Ta có : \(y' = \dfrac{{\sqrt {4 - {x^2}} - x\dfrac{{ - x}}{{\sqrt {4 - {x^2}} }}}}{{{{\left( {\sqrt {4 - {x^2}} } \right)}^2}}} = \dfrac{4}{{{{\left( {\sqrt {4 - {x^2}} } \right)}^3}}}\)
\( \Rightarrow y'\left( 0 \right) = \dfrac{1}{2}\).
Chọn đáp án đúng:
-
A.
\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
-
B.
\(\mathop {\lim }\limits_{x \to {x_0}} x = 1\)
-
C.
\(\mathop {\lim }\limits_{x \to {x_0}} c = {x_0}\)
-
D.
\(\mathop {\lim }\limits_{x \to {x_0}} x = 0\)
Đáp án : A
Ta có: \(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0},\mathop {\lim }\limits_{x \to {x_0}} c = c\) với \(c\) là hằng số.
Một số em có thể sẽ chọn nhầm đáp án C vì nhớ nhầm nhận xét giới hạn hàm số hằng.
Giá trị của giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[3]{{3{x^3} - 1}} + \sqrt {{x^2} + 2} } \right)\) là:
-
A.
\(\sqrt[3]{3} + 1.\)
-
B.
\( + \infty .\)
-
C.
\(\sqrt[3]{3} - 1.\)
-
D.
\( - \infty \).
Đáp án : B
Đặt \(x\) làm nhân tử chung.
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[3]{{3{x^3} - 1}} + \sqrt {{x^2} + 2} } \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt[3]{{3 - \dfrac{1}{{{x^3}}}}} + \sqrt {1 + \dfrac{2}{{{x^2}}}} } \right) = + \infty \) vì \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } x = + \infty \\\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[3]{{3 - \dfrac{1}{{{x^3}}}}} + \sqrt {1 + \dfrac{2}{{{x^2}}}} } \right) = \sqrt[3]{3} + 1 > 0\end{array} \right..\)
Giải nhanh: \(x \to + \infty :\,\,\sqrt[3]{{3{x^3} - 1}} + \sqrt {{x^2} + 2} \sim \sqrt[3]{{3{x^3}}} + \sqrt {{x^2}} = \left( {\sqrt[3]{3} + 1} \right)x \to + \infty .\)
Biết rằng \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1.\) Tìm giá trị thực của tham số \(m\) để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}}}&{{\rm{khi }}x \ne \pi }\\m&{{\rm{khi }}x = \pi }\end{array}} \right.$ liên tục tại \(x = \pi .\)
-
A.
\(m = \dfrac{\pi }{2}.\)
-
B.
\(m = - \dfrac{\pi }{2}.\)
-
C.
\(m = \dfrac{1}{2}.\)
-
D.
\(m = - \dfrac{1}{2}.\)
Đáp án : C
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hàm số xác định với mọi \(x \in \mathbb{R}\). Điều kiện của bài toán trở thành:
$m = f\left( \pi \right) = \mathop {\lim }\limits_{x \to \pi } f\left( x \right)$ $ = \mathop {\lim }\limits_{x \to \pi } \dfrac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}} = \mathop {\lim }\limits_{x \to \pi } \dfrac{{2{{\cos }^2}\dfrac{x}{2}}}{{{{\left( {x - \pi } \right)}^2}}}$ $ = \mathop {\lim }\limits_{x \to \pi } \dfrac{{2{{\sin }^2}\left( {\dfrac{x}{2} - \dfrac{\pi }{2}} \right)}}{{{{\left( {x - \pi } \right)}^2}}}$ $ = \mathop {\lim }\limits_{x \to \pi } \frac{{\frac{1}{4}.2{{\sin }^2}\left( {\frac{x}{2} - \frac{\pi }{2}} \right)}}{{\frac{1}{4}.{{\left( {x - \pi } \right)}^2}}} $ $= \mathop {\lim }\limits_{x \to \pi } \frac{{\frac{1}{2}{{\sin }^2}\left( {\frac{x}{2} - \frac{\pi }{2}} \right)}}{{{{\left( {\frac{{x - \pi }}{2}} \right)}^2}}}$ $ = \frac{1}{2}\mathop {\lim }\limits_{x \to \pi } \frac{{{{\sin }^2}\left( {\frac{x}{2} - \frac{\pi }{2}} \right)}}{{{{\left( {\frac{x}{2} - \frac{\pi }{2}} \right)}^2}}}$ $ = \dfrac{1}{2}\mathop {\lim }\limits_{x \to \pi } {\left[ {\dfrac{{\sin \left( {\dfrac{x}{2} - \dfrac{\pi }{2}} \right)}}{{\left( {\dfrac{x}{2} - \dfrac{\pi }{2}} \right)}}} \right]^2}\,\,\left( * \right)$
Đặt \(t = \dfrac{x}{2} - \dfrac{\pi }{2} \to 0\) khi \(x \to 1.\) Khi đó $\left( * \right)$ trở thành: \(m = \dfrac{1}{2}\mathop {\lim }\limits_{t \to 0} {\left( {\dfrac{{\sin t}}{t}} \right)^2} = \dfrac{1}{2}{.1^2} = \dfrac{1}{2}.\)
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân ở \(C\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AB\) và \(SB\). Biết \(HK \bot \left( {ABC} \right)\), khẳng định nào sau đây sai?
-
A.
\(CH \bot HK\).
-
B.
\(AB \bot \left( {CHK} \right)\).
-
C.
\(CH \bot AK\).
-
D.
\(BC \bot \left( {SAC} \right)\).
Đáp án : D
Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh \(CH \bot \left( {SAB} \right)\).
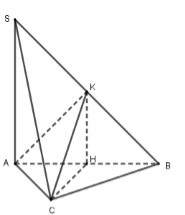
Ta có: \(HK \bot \left( {ABC} \right) \Rightarrow HK \bot CH\) hay A đúng.
Do \(\Delta ABC\) cân tại \(C\) nên \(CH \bot AB\).
Mà \(HK \bot \left( {ABC} \right) \Rightarrow SA \bot \left( {ABC} \right) \Rightarrow SA \bot CH\).
Do đó \(CH \bot \left( {SAB} \right) \Rightarrow CH \bot AK\) hay C đúng.
Ngoài ra \(HK \bot AB\), mà \(AB \bot CH\) \( \Rightarrow AB \bot \left( {CHK} \right)\) hay B đúng.
D sai vì \(BC\) không vuông góc với \(AC\) nên không có \(BC \bot \left( {SAC} \right)\).
Cho chóp đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 3. Gọi \(\varphi \) là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?
-
A.
\(\tan \varphi = \sqrt 7 \)
-
B.
\(\varphi = {60^0}\)
-
C.
\(\varphi = {45^0}\)
-
D.
\(\tan \varphi = \dfrac{{\sqrt {14} }}{2}\)
Đáp án : D
Xác định hình chiếu của S lên mặt phẳng đáy, từ đó xác định được góc và tính số đo.

Gọi \(O\) là tâm mặt đáy \(\left( {ABCD} \right)\) , suy ra \(SO \bot \left( {ABCD} \right)\).
Vì \(SO \bot \left( {ABCD} \right)\), suy ra \(OA\) là hình chiếu của \(SA\) trên mặt phẳng \(\left( {ABCD} \right)\).
Do đó \(\widehat {\left( {SA,\left( {ABCD} \right)} \right)} = \widehat {\left( {SA,AO} \right)} = \widehat {SAO}\).
Đáy ABCD là hình vuông nên \(BO=OA=\sqrt 2\).
Tam giác vuông \(SOA\), có:
\(\tan \widehat {SAO} = \dfrac{{SO}}{{AO}} = \dfrac{{\sqrt {S{B^2} - B{O^2}} }}{{\sqrt 2}} = \dfrac{{\sqrt {14} }}{2}\).
Tìm tập xác định của hàm số sau \(y = \tan \left( {2x + \dfrac{\pi }{3}} \right)\).
-
A.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{4} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{{12}} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{8} + k\dfrac{\pi }{2};k \in \mathbb{Z}} \right\}\)
Đáp án : C
Hàm số \(y = \tan u\left( x \right)\) xác định nếu \(\cos u\left( x \right) \ne 0 \Leftrightarrow u\left( x \right) \ne \dfrac{\pi }{2} + k\pi \).
Điều kiện: \(\cos \left( {2x + \dfrac{\pi }{3}} \right) \ne 0 \Leftrightarrow 2x + \dfrac{\pi }{3} \ne \dfrac{\pi }{2} + k\pi \Leftrightarrow x \ne \dfrac{\pi }{{12}} + k\dfrac{\pi }{2}\)
Số điện thoại ở Huyện Củ Chi có $7$ chữ số và bắt đầu bởi $3$ chữ số đầu tiên là $790$. Hỏi ở Huyện Củ Chi có tối đa bao nhiêu máy điện thoại:
-
A.
$1000$.
-
B.
$100000$.
-
C.
$10000$.
-
D.
$1000000$.
Đáp án : C
- Đếm số cách chọn từng chữ số trong bốn số cuối số điện thoại.
- Sử dụng quy tắc nhân và tính số cách chọn.
Gọi số điện thoại cần tìm có dạng \(\overline {790abcd} \).
Khi đó: \(a\)có 10 cách chọn, \(b\)có 10 cách chọn, \(c\)có 10 cách chọn, \(d\) có 10 cách chọn.
Nên có tất cả \(10.10.10.10 = {10^4}\) số.
Nghiệm của phương trình: \(\sin 2x - \sqrt 3 \sin x = 0\) là:
-
A.
\(\left[ \begin{array}{l}x = k\pi \\x = \pm \dfrac{\pi }{6} + k2\pi \end{array} \right.\).
-
B.
\(\left[ \begin{array}{l}x = k\pi \\x = \pm \dfrac{\pi }{6} + k\pi \end{array} \right.\).
-
C.
\(\left[ \begin{array}{l}x = k2\pi \\x = \pm \dfrac{\pi }{3} + k2\pi \end{array} \right.\).
-
D.
\(x = \pm \dfrac{\pi }{6} + k2\pi \).
Đáp án : A
Bước 1: Biến đổi phương trình về dạng tích
Sử dụng công thức \(\sin 2x=2\sin x.\cos x\)
Bước 2: Giải phương trình tích và kết luận nghiệm.
Sử dụng công thức:
$\sin x = 0 \Leftrightarrow x=k\pi$
$\cos x=\cos a \Leftrightarrow x=\pm a+k2\pi$
Bước 1:
\(\sin 2x - \sqrt 3 \sin x = 0\)\( \Leftrightarrow 2\sin x\cos x - \sqrt 3 \sin x = 0\)
\( \Leftrightarrow \sin x\left( {2\cos x - \sqrt 3 } \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = \dfrac{{\sqrt 3 }}{2}\end{array} \right.\)
Bước 2:
\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = \cos \dfrac{\pi }{6}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \pm \dfrac{\pi }{6} + k2\pi \end{array} \right.,k \in \mathbb{Z}\)
Số các hoán vị của \(17\) phần tử là:
-
A.
\({17^2}\)
-
B.
\(17!\)
-
C.
\(17.16\)
-
D.
\(17\)
Đáp án : B
Sử dụng công thức tính số các hoán vị của \(n\) phần tử \({P_n} = n!\)
Số các hoán vị khác nhau của \(17\) phần tử là \(17!\).
Đội thanh niên xung kích của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp \(A\), 4 học sinh lớp \(B\) và 3 học sinh lớp \(C\). Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong 3 lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
-
A.
\(120.\)
-
B.
\(90.\)
-
C.
\(270.\)
-
D.
\(225.\)
Đáp án : D
Liệt kê các trường hợp có thể xảy ra, đếm số cách chọn trong mỗi trường hợp và kết luận.
Số cách chọn 4 học sinh bất kì từ 12 học sinh là \(C_{12}^4 = 495\) cách.
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau:
\( * \) TH1: Lớp \(A\) có hai học sinh, các lớp \(B,C\) mỗi lớp có 1 học sinh:
Chọn 2 học sinh trong 5 học sinh lớp \(A\) có \(C_5^2\) cách.
Chọn 1 học sinh trong 4 học sinh lớp \(B\) có \(C_4^1\) cách.
Chọn 1 học sinh trong 3 học sinh lớp \(C\) có \(C_3^1\) cách.
Suy ra số cách chọn là \(C_5^2.C_4^1.C_3^1 = 120\) cách.
\( * \) TH2: Lớp \(B\) có 2 học sinh, các lớp \(A,C\) mỗi lớp có 1 học sinh:
Tương tự ta có số cách chọn là \(C_5^1.C_4^2.C_3^1 = 90\) cách.
\( * \) TH3: Lớp \(C\) có 2 học sinh, các lớp \(A,B\) mỗi lớp có 1 học sinh:
Tương tự ta có số cách chọn là \(C_5^1.C_4^1.C_3^2 = 60\) cách.
Vậy số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là \(120 + 90 + 60 = 270\) cách.
Số cách chọn ra 4 học sinh thuộc không quá 2 trong 3 lớp trên là \(495 - 270 = 225\) cách.
Tính tổng \(S = C_{100}^0 - 5C_{100}^1 + {5^2}C_{100}^2 - ... + {5^{100}}C_{100}^{100}\)
-
A.
\({6^{100}}\).
-
B.
\({4^{100}}\).
-
C.
\({2^{300}}\).
-
D.
\({3^{200}}\).
Đáp án : B
Sử dụng khai triển \({\left( {a + b} \right)^n}\) và thay \(a,b\) bởi các giá trị thích hợp tính tổng.
Nhận thấy \({\left( { - 5} \right)^k}C_{100}^k\) là hệ số của \({x^k}\) trong khai triển \({\left( {1 - 5x} \right)^{100}}\)
Vì thế xét \(P\left( x \right) = {\left( {1 - 5x} \right)^{100}}\), theo khai triển nhị thức Newton, ta có:
\(P\left( x \right) = {\left( {1 - 5x} \right)^{100}} = C_{100}^0 - C_{100}^15x + C_{100}^2{\left( {5x} \right)^2} - ... + C_{100}^{100}{\left( {5x} \right)^{100}}\)
Thay \(x = 1\) vào ta được:
\(P\left( x \right) = {\left( 4 \right)^{100}} = C_{100}^0 - C_{100}^15 + C_{100}^2{5^2} - ... + C_{100}^{100}{5^{100}}\)
Ta cũng có thể xét khai triển \({\left( {1 + 5x} \right)^{100}}\) rồi sau đó thay \(x = - 1\) vào.
Một lô hàng gồm $1000$ sản phẩm, trong đó có $50$ phế phẩm. Lấy ngẫu nhiên từ lô hàng đó $1$ sản phẩm. Xác suất để lấy được sản phẩm tốt là:
-
A.
$0,94.$
-
B.
$0,96.$
-
C.
$0,95.$
-
D.
$0,97.$
Đáp án : C
- Tính số phần tử của không gian mẫu.
- Tính số khả năng có lợi cho biến cố.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Gọi A là biến cố: “lấy được 1 sản phẩm tốt.“
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{1000}^1 = 1000.\)
Số cách lấy được sản phẩm tốt là \(n\left( A \right) = C_{950}^1 = 950.\)
=> \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{950}}{{1000}} = 0,95.\)
Một con xúc sắc cân đối và đồng chất được gieo ba lần. Gọi $P$ là xác suất để tổng số chấm xuất hiện ở hai lần gieo đầu bằng số chấm xuất hiện ở lần gieo thứ ba. Khi đó $P$ bằng:
-
A.
$\dfrac{{10}}{{216}}$.
-
B.
$\dfrac{{15}}{{216}}$.
-
C.
$\dfrac{{16}}{{216}}$.
-
D.
$\dfrac{{12}}{{216}}$.
Đáp án : B
- Tính số phần tử của không gian mẫu \(n\left( \Omega \right)\).
- Liệt kê các khả năng có lợi cho biến cố.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
$n(\Omega ) = 6.6.6 = 216$. Gọi $A$:”tổng số chấm xuất hiện ở hai lần gieo đầu bằng số chấm xuất hiện ở lần gieo thứ ba”.
Ta chỉ cần chọn 1 bộ 2 số chấm ứng với hai lần gieo đầu sao cho tổng của chúng thuộc tập $\{ 1;2;3;4;5;6\} $ và số chấm lần gieo thứ ba sẽ là tổng hai lần gieo đầu.
Liệt kê ra ta có:
${\rm{\{ (1;1);(1;2);(1;3);(1;4);(1;5);(2;1);(2;2);(2;3);(2;4);(3;1);(3;2);(3;3);(4;1);(4;2);(5;1)\} }}$
Do đó $n(A) = 15$. Vậy $P(A) = \dfrac{{15}}{{216}}$.
Cho dãy số $\dfrac{1}{2};0; - \dfrac{1}{2}; - 1; - \dfrac{3}{2}$ là cấp số cộng với:
-
A.
Số hạng đầu tiên là $\dfrac{1}{2}$, công sai là $\dfrac{1}{2}.$
-
B.
Số hạng đầu tiên là $\dfrac{1}{2}$, công sai là $ - \dfrac{1}{2}.$
-
C.
Số hạng đầu tiên là $0$, công sai là $\dfrac{1}{2}.$
-
D.
Số hạng đầu tiên là $0$, công sai là $ - \dfrac{1}{2}.$
Đáp án : B
Nếu dãy số \(\left( {{u_n}} \right)\) là một cấp số cộng thì công sai \(d\) của nó là hiệu của một cặp số hạng liên tiếp bất kì (số hạng sau trừ cho số hạng trước) của dãy số đó.
Ta có $\dfrac{1}{2};0; - \dfrac{1}{2}; - 1; - \dfrac{3}{2}$ là cấp số cộng \( \Rightarrow \left\{ \begin{array}{l}{u_1} = \dfrac{1}{2}\\{u_2} - {u_1} = - \dfrac{1}{2} = d\end{array} \right.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\). Mệnh đề nào dưới đây là mệnh đề đúng
-
A.
\(\left( {n - p} \right){u_m} + \left( {p - m} \right){u_n} + \left( {m - n} \right){u_p} = 0\).
-
B.
\(\left( {m - n} \right){u_m} + \left( {n - p} \right){u_n} + \left( {p - m} \right){u_p} = 0\).
-
C.
\(\left( {m - p} \right){u_m} + \left( {n - m} \right){u_n} + \left( {p - n} \right){u_p} = 0\).
-
D.
\(\left( {p - n} \right){u_m} + \left( {m - p} \right){u_n} + \left( {m - n} \right){u_p} = 0\).
Đáp án : A
Kiểm tra từng phương án cho đến khi tìm được phương án đúng:
Sử dụng công thức số hạng tổng quát để biểu diễn $u_m;u_n;u_p$ rồi thay vào từng đáp án và biến đổi.
Ta có: \({u_m} = {u_1} + \left( {m - 1} \right)d;\,{u_n} = {u_1} + \left( {n - 1} \right)d;\,{u_p} = {u_1} + \left( {p - 1} \right)d\)
Xét phương án A:
Ta có: \(\left( {n - p} \right){u_m} + \left( {p - m} \right){u_n} + \left( {m - n} \right){u_p}\)
\( = \left( {n - p} \right)\left[ {{u_1} + \left( {m - 1} \right)d} \right] \)\(+ \left( {p - m} \right)\left[ {{u_1} + \left( {n - 1} \right)d} \right] \)\(+ \left( {m - n} \right)\left[ {{u_1} + \left( {p - 1} \right)d} \right]\)
$= \left( {n - p} \right)u_1+ \left( {n - p} \right) \left( {m - 1} \right)d$$+ \left( {p-m} \right)u_1+ \left( {p-m} \right) \left( {n - 1} \right)d$$+ \left( {m-n} \right)u_1+ \left( {m-n} \right) \left( {p - 1} \right)d$
$= \left( {n - p+p-m+m-n} \right)u_1+ \left[ { \left( {n-p} \right) \left( {m - 1} \right)+\left( {p-m} \right) \left( {n - 1} \right)+\left( {m-n} \right) \left( {p - 1} \right)} \right]d$
$=0.u_1+0.d$
$=0$
Vậy đáp án A.
Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là:
-
A.
$720$
-
B.
$81$
-
C.
$64$
-
D.
$56$
Đáp án : B
Tính \(q\) và suy ra số hạng tiếp theo, dựa vào công thức \({u_{n + 1}} = q{u_n}\).
Ta có cấp số nhân \(\left( {{u_n}} \right)\) có:
\(\,\left\{ \begin{array}{l}{u_k} = 16\\{u_{k + 1}} = 36\end{array} \right. \Rightarrow q = \dfrac{{{u_{k + 1}}}}{{{u_k}}} = \dfrac{9}{4}\)\( \Rightarrow {u_{k + 2}} = {u_{k + 1}}q = 81\)
Các em cũng có thể sử dụng công thức \(u_k^2 = {u_{k + 1}}.{u_{k - 1}}\).
Có bao nhiêu số nguyên \(m \in \left[ { - 5;5} \right]\) để \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\).
-
A.
$6$
-
B.
$4$
-
C.
$3$
-
D.
$5$
Đáp án : B
Xét hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + m\) trên \(\left[ {1;3} \right]\), lập BBT từ đó xét các trường hợp.
Xét hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + m\) trên \(\left[ {1;3} \right]\), có \(f'\left( x \right) = 3{x^2} - 6x,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\left( L \right)\\x = 2\end{array} \right.\)
Bảng biến thiên:
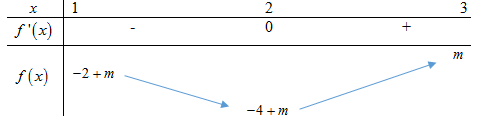
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Rightarrow \left[ \begin{array}{l}m - 4 > 0\\m < 0\end{array} \right.\)
TH1: \(m - 4 > 0 \Leftrightarrow m > 4\)
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Leftrightarrow m - 4 \ge 2 \Leftrightarrow m \ge 6\)
Mà \(m \in \left[ { - 5;5} \right] \Rightarrow m \in \emptyset \)
TH2: \(m < 0\)
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Leftrightarrow - m \ge 2 \Leftrightarrow m \le - 2\)
Mà \(m \in \left[ { - 5;5} \right],m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 5; - 4; - 3; - 2} \right\}\): 4 giá trị.
Giải thích chi tiết chỗ \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Rightarrow \left[ \begin{array}{l}m - 4 > 0\\m < 0\end{array} \right.\)
+) Nếu \(m-4 \le 0 < m-2\) thì đồ thị hàm số \(y=|f(x)|\) có dáng như hình dưới. Khi đó \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| =0 \) nên không thỏa mãn.
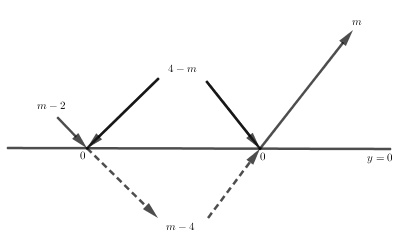
+) Nếu \(m-2 < 0 \le m\) thì đồ thị hàm số \(y=|f(x)|\) có dáng như hình dưới. Khi đó \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| =0 \) nên không thỏa mãn.
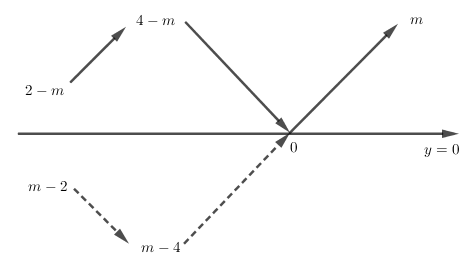
Cho phương trình \(\left( {2\sin x - 1} \right)\left( {\sqrt 3 \tan x + 2\sin x} \right) = 3 - 4{\cos ^2}x\). Tổng tất cả các nghiệm thuộc đoạn \(\left[ {0;\,20\pi } \right]\) của phương trình bằng
-
A.
\(\dfrac{{1150}}{3}\pi \).
-
B.
\(\dfrac{{570}}{3}\pi \).
-
C.
\(\dfrac{{880}}{3}\pi \).
-
D.
\(\dfrac{{875}}{3}\pi \).
Đáp án : D
- Sử dụng các công thức nhân ba, phân tích tích thành tổng để biến đổi đơn giản phương trình.
- Giải phương trình, tìm nghiệm thỏa mãn bài toán và tính tổng các nghiệm.
\(\left( {2\sin x - 1} \right)\left( {\sqrt 3 \tan x + 2\sin x} \right) = 3 - 4{\cos ^2}x\,\,\left( * \right)\)
Điều kiện: \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \).
\(\begin{array}{l}\left( * \right) \Leftrightarrow \left( {2\sin x - 1} \right).\dfrac{{\sqrt 3 \sin x + 2\sin x\cos x}}{{\cos x}} = 3 - 4{\cos ^2}x\\ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sqrt 3 \sin x + \sin 2x} \right) + \left( {4{{\cos }^3}x - 3\cos x} \right) = 0\\ \Leftrightarrow 2\sqrt 3 {\sin ^2}x - \sqrt 3 \sin x + 2\sin x\sin 2x - \sin 2x + \cos 3x = 0\\ \Leftrightarrow 2\sqrt 3 {\sin ^2}x - \sqrt 3 \sin x + \cos x - \cos 3x - \sin 2x + \cos 3x = 0\\ \Leftrightarrow \sqrt 3 \sin x\left( {2\sin x - 1} \right) - \sin 2x + \cos x = 0\\ \Leftrightarrow \sqrt 3 \sin x\left( {2\sin x - 1} \right) - \cos x\left( {2\sin x - 1} \right) = 0\\ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sqrt 3 \sin x - \cos x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2\sin x - 1 = 0\,\,\left( 1 \right)\\\sqrt 3 \sin x - \cos x = 0\,\,\left( 2 \right)\end{array} \right.\end{array}\)
Giải \(\left( 1 \right) \Leftrightarrow \sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\).
Giải \(\left( 2 \right) \Leftrightarrow \sqrt 3 \sin x = \cos x \Leftrightarrow \sqrt 3 \tan x = 1 \Leftrightarrow \tan x = \dfrac{1}{{\sqrt 3 }} \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \left( {TM} \right)\).
Hợp nghiệm của \(\left( 1 \right)\) và \(\left( 2 \right)\) ta được \(\left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Mà \(x \in \left[ {0;20\pi } \right] \Rightarrow x \in \left\{ {\dfrac{\pi }{6};\dfrac{\pi }{6} + \pi ;...;\dfrac{\pi }{6} + 19\pi ;\dfrac{{5\pi }}{6};\dfrac{{5\pi }}{6} + 2\pi ;...\dfrac{{5\pi }}{6} + 18\pi } \right\}\)
Vậy tổng các nghiệm là:
\(\begin{array}{l}\,\,\,\,\,\dfrac{\pi }{6} + \dfrac{\pi }{6} + \pi + \dfrac{\pi }{6} + 2\pi + ... + \dfrac{\pi }{6} + 19\pi + \dfrac{{5\pi }}{6} + \dfrac{{5\pi }}{6} + 2\pi + ... + \dfrac{{5\pi }}{6} + 18\pi \\ = 20.\dfrac{\pi }{6} + \left( {1 + 2 + 3 + ... + 19} \right)\pi + \dfrac{{5\pi }}{6}.10 + 2\pi \left( {1 + 2 + ... + 9} \right) = \dfrac{{875\pi }}{3}\end{array}\).
Cho tứ diện \(ABCD\) có \(AB = CD = 4,BC = AD = 5,AC = BD = 6\). \(M\) là điểm thay đổi trong tâm giác \(ABC\). Các đường thẳng qua \(M\) song song với \(AD,BD,CD\) tương ứng cắt mặt phẳng \(\left( {BCD} \right),\left( {ACD} \right),\left( {ABD} \right)\) tại \(A',B',C'\). Giá trị lớn nhất của \(MA'.MB'.MC'\) là
-
A.
\(\dfrac{{40}}{9}\)
-
B.
\(\dfrac{{24}}{9}\)
-
C.
\(\dfrac{{30}}{9}\)
-
D.
\(\dfrac{{20}}{9}\)
Đáp án : A
- Kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
- Dựng các đường thẳng qua \(M\) và song song với \(AD,BD,CD\) suy ra các điểm \(A',B',C'\).
- Sử dụng định lý Ta – let tính \(MA',MB',MC'\).
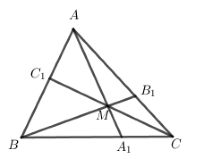
- Sử dụng hệ thức \(\dfrac{{{A_1}M}}{{AM}} + \dfrac{{{B_1}M}}{{BM}} + \dfrac{{{C_1}M}}{{CM}} = 1\) đánh giá GTLN của tích \(MA'.MB'.MC'\).
ở đó, \(M\) là một điểm nằm trong tam giác \(ABC\) và \({A_1},{B_1},{C_1}\) lần lượt là các giao điểm của \(AM,BM,CM\) với các cạnh \(BC,CA,AB\).
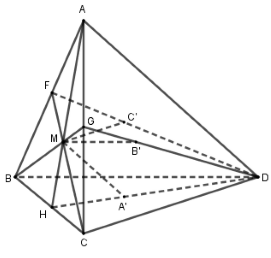
Trong tam giác \(ABC\), kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
+) Trong mặt phẳng \(\left( {HAD} \right)\), kẻ \(MA'//AD\).
+) Trong mặt phẳng \(\left( {GBD} \right)\), kẻ \(MB'//BD\).
+) Trong mặt phẳng \(\left( {FCD} \right)\), kẻ \(MC'//CD\).
Từ đó ta được các điểm \(A',B',C'\) cần tìm.
Theo định lý Ta – let ta có: \(\dfrac{{MA'}}{{AD}} = \dfrac{{HM}}{{HA}} \Rightarrow MA' = 5.\dfrac{{MH}}{{AH}}\)
\(\dfrac{{MB'}}{{BD}} = \dfrac{{GM}}{{GB}} \Rightarrow MB' = 6.\dfrac{{MG}}{{BG}}\); \(\dfrac{{MC'}}{{CD}} = \dfrac{{FM}}{{FC}} \Rightarrow MC' = 4.\dfrac{{MF}}{{CF}}\)
\( \Rightarrow MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}\).
Trong tam giác \(ABC\) ta có: \(1 = \dfrac{{MH}}{{AH}} + \dfrac{{MG}}{{BG}} + \dfrac{{MF}}{{CF}} \ge 3\sqrt[3]{{\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}}}\) \( \Rightarrow \dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le \dfrac{1}{{27}}\)
Do đó \(MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le 120.\dfrac{1}{{27}} = \dfrac{{40}}{9}\)\( \Rightarrow {\left( {MA'.MB'.MC'} \right)_{\max }} = \dfrac{{40}}{9}\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Đáp án : A
Dựa vào đồ thị hàm số suy ra các khoảng đồng biến và nghịch biến của hàm số \(y = f\left( x \right)\) từ đó suy ra tính đồng biến và nghịch biến của hàm số \(y = - 2f\left( x \right)\).
Dựa vào đồ thị hàm số ta có \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;2} \right)\), suy ra f'(x) < 0 trên khoảng (0; 2).
Xét hàm số: \(y = - 2f\left( x \right)\) ta có: \(y' = - 2f'\left( x \right)\).
Hàm số \(y = - 2f\left( x \right)\) đồng biến khi \(y' > 0 \Leftrightarrow - 2f'\left( x \right) > 0 \Leftrightarrow f'\left( x \right) < 0 \Leftrightarrow 0 < x < 2\).
Vậy hàm số \(y = - 2f\left( x \right)\) đồng biến \( \Leftrightarrow x \in \left( {0;2} \right)\).
Xét các đáp án thấy chỉ có khoảng (1; 2) thuộc (0; 2) nên đáp án A đúng.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận