Câu hỏi
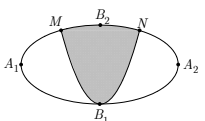
Một biển quảng cáo có dạng hình elip với bốn đỉnh \({A_1},\,{A_2},\,{B_1},\,{B_2}\) như hình vẽ bên. Người ta chia elip bởi parabol có đỉnh \({B_1}\), trục đối xứng \({B_1}{B_2}\) và đi qua các điểm \(M,N\) . Sau đó sơn phần tô đậm với giá \(200.000\) đồng/\({m^2}\) và trang trí phần đèn led còn lại với giá \(500000\) đồng/\(m^2\). Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng \({A_1}{A_2} = 4m,\,{B_1}{B_2} = 2m,\,MN = 2m.\)
- A \(2.341.000\) đồng
- B \(2.057.000\) đồng
- C \(2.760.000\) đồng
- D \(1.664.000\) đồng
Phương pháp giải:
+) Gắn trục tọa độ Oxy, xác định phương trình Elip và phương trình Parabol.
+) Ứng dụng tích phân để tính diện tích phần tô đậm \({S_1}\).
+) Tính diện tích phần không tô đậm: \({S_2} = {S_{\left( E \right)}} - {S_1}\).
+) Tính kinh phí.
Lời giải chi tiết:
Gắn hệ trục tọa độ như hình vẽ.
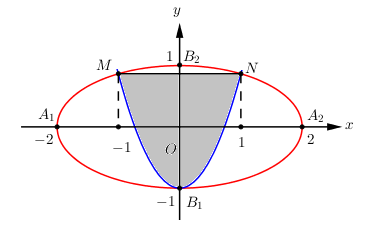
Phương trình elip : \(\left( E \right):\,\,\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{1} = 1 \Leftrightarrow {x^2} + 4{y^2} = 4 \Leftrightarrow y = \pm \dfrac{{\sqrt {4 - {x^2}} }}{2}\).
Do \(MN = 2 \Rightarrow {x_N} = 1,\,\,{x_M} = - 1\).
Thay \(x = - 1\) vào phương trình \(\left( E \right) \Rightarrow 1 + 4{y^2} = 4 \Leftrightarrow 4{y^2} = 3 \Leftrightarrow y = \dfrac{{ \pm \sqrt 3 }}{2} \Rightarrow M\left( { - 1;\dfrac{{\sqrt 3 }}{2}} \right)\).
Thay \(x = 1\) vào phương trình \(\left( E \right) \Rightarrow 1 + 4{y^2} = 4 \Leftrightarrow 4{y^2} = 3 \Leftrightarrow y = \dfrac{{ \pm \sqrt 3 }}{2} \Rightarrow N\left( {1;\dfrac{{\sqrt 3 }}{2}} \right)\).
Gọi phương trình Parabol là \(y = a{x^2} + bx + c\,\,\left( P \right)\).
\(\left( P \right)\) đi qua các điểm \(\left( {0; - 1} \right);\,\,\left( {1;\dfrac{{\sqrt 3 }}{2}} \right);\,\,\left( { - 1;\dfrac{{\sqrt 3 }}{2}} \right)\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}c = - 1\\a + b + c = \dfrac{{\sqrt 3 }}{2}\\a - b + c = \dfrac{{\sqrt 3 }}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = - 1\\a + c = \dfrac{{\sqrt 3 }}{2}\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{{\sqrt 3 }}{2} + 1\\b = 0\\c = - 1\end{array} \right. \Rightarrow \left( P \right):\,\,y = \left( {\dfrac{{\sqrt 3 }}{2} + 1} \right){x^2} - 1\)
Do đó diện tích phần tô đậm là \({S_1} = \int\limits_{ - 1}^1 {\left( {\dfrac{{\sqrt {4 - {x^2}} }}{2} - \left( {\dfrac{{\sqrt 3 }}{2} + 1} \right){x^2} + 1} \right)dx} \approx 2,6692\).
Diện tích Elip là \({S_E} = \pi ab = \pi .2.1 = 2\pi \Rightarrow \) Diện tích phần còn lại để trang trí đèn led là \({S_2} = {S_{\left( E \right)}} - {S_1} \approx 3,6140\).
Vậy kinh phí là: \(200\,\,000.{S_1} + 500\,\,000.{S_2} \approx 2\,\,340\,\,840 \approx 2\,\,341\,\,000\) (đồng).
Chọn A.