Lời giải chi tiết:

Ta có \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = 2 \Leftrightarrow {31^x} + {3^x} + mx \ge 2\,\,\forall x \in \mathbb{R}\).

\( \Leftrightarrow mx \ge 2 - {31^x} - {3^x} \Leftrightarrow \left\{ \begin{array}{l}m \ge \dfrac{{2 - {{31}^x} - {3^x}}}{x}\,\,khi\,\,x > 0\\m \le \dfrac{{2 - {{31}^x} - {3^x}}}{x}\,\,khi\,\,x < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge \mathop {\min }\limits_{\left( {0; + \infty } \right)} g\left( x \right)\\m \le \mathop {\max }\limits_{\left( { - \infty ;0} \right)} g\left( x \right)\end{array} \right.\) với \(g\left( x \right) = \dfrac{{2 - {{31}^x} - {3^x}}}{x}\,\,\left( {x \in \mathbb{R}\backslash \left\{ 0 \right\}} \right)\).

Xét hàm số \(g\left( x \right) = \dfrac{{2 - {{31}^x} - {3^x}}}{x}\,\,\left( {x \in \mathbb{R}\backslash \left\{ 0 \right\}} \right)\) ta có :

\(g'\left( x \right) = \dfrac{{\left( { - {{31}^x}\ln 31 - {3^x}\ln 3} \right)x - \left( {2 - {{31}^x} - {3^x}} \right)}}{{{x^2}}}\).

Đặt \(h\left( x \right) = \left( { - {{31}^x}\ln 31 - {3^x}\ln 3} \right)x - \left( {2 - {{31}^x} - {3^x}} \right)\)

\(\begin{array}{l} \Rightarrow h'\left( x \right) = \left( { - {{31}^x}{{\ln }^2}31 - {3^x}{{\ln }^2}3} \right)x - \left( { - {{31}^x}\ln 31 - {3^x}\ln 3} \right) - \left( { - {{31}^x}\ln 31 - {3^x}\ln 3} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( { - {{31}^x}{{\ln }^2}31 - {3^x}{{\ln }^2}3} \right)x = 0 \Leftrightarrow x = 0\end{array}\)

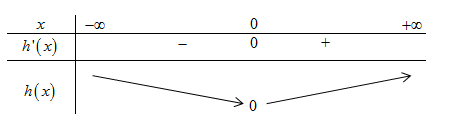
BBT:

Từ BBT \( \Rightarrow h\left( x \right) \ge 0\,\,\forall x \in \mathbb{R}\), \(h\left( x \right) = 0 \Leftrightarrow x = 0\).

\( \Rightarrow h\left( x \right) > 0\,\,\forall x \in \mathbb{R}\backslash \left\{ 0 \right\} \Rightarrow g'\left( x \right) = \dfrac{{h\left( x \right)}}{{{x^2}}} > 0\,\,\forall x \in \mathbb{R}\backslash \left\{ 0 \right\}\).

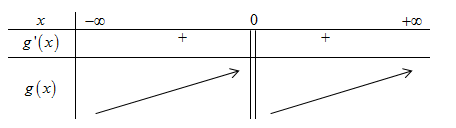
\( \Rightarrow \) Hàm số \(y = g\left( x \right)\) đồng biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).

BBT:

Từ BBT

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}m \ge \mathop {\lim }\limits_{x \to {0^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{2 - {{31}^x} - {3^x}}}{x} =  - \left[ {\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{{{31}^x} - 1}}{x} + \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{{3^x} - 1}}{x}} \right] =  - \ln 31 - \ln 3\\m \le \mathop {\lim }\limits_{x \to {0^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{2 - {{31}^x} - {3^x}}}{x} =  - \left[ {\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{31}^x} - 1}}{x} + \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{{3^x} - 1}}{x}} \right] =  - \ln 31 - \ln 3\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}m \ge  - \ln 31 - \ln 3\\m \le  - \ln 31 - \ln 3\end{array} \right. \Leftrightarrow m =  - \ln 31 - \ln 3 \approx  - 4,53\end{array}\)

Chọn B.