Phương pháp giải:

+) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách:

+) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\)

+) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\)  Khi đó:

\(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) 

Lời giải chi tiết:

Ta có: \(f'\left( x \right) = x\left( {x + 1} \right){\left( {x - 2} \right)^2}\)

\( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\left( {boi\,\,1} \right)\\x =  - 1\,\,\,\left( {boi\,\,1} \right)\\x = 2\,\,\,\left( {boi\,\,2} \right)\end{array} \right.\)

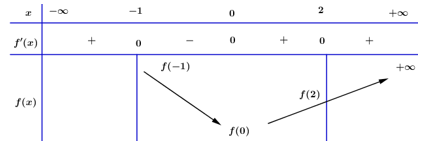
Ta có BBT:

Vậy giá trị nhỏ nhất của hàm số là: \(\mathop {Min}\limits_{\left[ { - 1;\,2} \right]} \,y = f\left( 0 \right).\)

Chọn B.