Câu hỏi
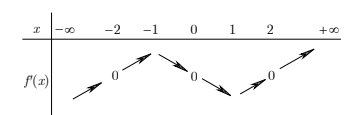
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số \(g\left( x \right) = f\left( {2x} \right) - {\sin ^2}x\) trên đoạn \(\left[ { - 1;1} \right]\) là
- A \(f\left( { - 1} \right)\)
- B \(f\left( 0 \right)\)
- C \(f\left( 2 \right)\)
- D \(f\left( 1 \right)\)
Phương pháp giải:
+) Từ BBT của hàm số \(f'\left( x \right)\) ta suy ra BBT của hàm số \(f\left( x \right)\).
+) Đánh giá \( - 1 + f\left( {2x} \right) \le g\left( x \right) \le f\left( {2x} \right)\). Dựa vào BBT hàm số \(f\left( x \right)\) xác định giá trị lớn nhất của \(f\left( {2x} \right)\,\,\forall x \in \left[ { - 1;1} \right]\).
Lời giải chi tiết:
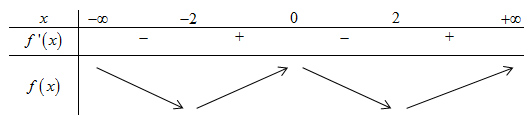
Từ BBT của hàm số \(f'\left( x \right)\) ta suy ra BBT của hàm số \(f\left( x \right)\) như sau:
Ta có \(g\left( x \right) = f\left( {2x} \right) - {\sin ^2}x\).
Do \(0 \le {\sin ^2}x \le 1 \Leftrightarrow - 1 \le - {\sin ^2}x \le 0 \Leftrightarrow - 1 + f\left( {2x} \right) \le g\left( x \right) \le f\left( {2x} \right)\).
Vì \(x \in \left[ { - 1;1} \right] \Rightarrow 2x \in \left[ { - 2;2} \right] \Rightarrow f\left( {2x} \right) \le f\left( 0 \right)\,\,\forall x \in \left[ { - 2;2} \right]\).
\( \Rightarrow g\left( x \right) \le f\left( 0 \right)\).
Chọn B.