Câu hỏi
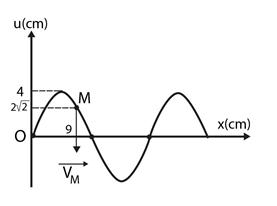
Một sóng cơ truyền trên sợi dây dài theo trục Ox. Tại một thời điểm nào đó sợi dây có dạng như hình vẽ, phần tử tại M đang đi xuống với tốc độ cm/s. Biết rằng khoảng cách từ vị trí cân bằng của phần tử tại M đến vị trí cân bằng của phần tử tại O là 9cm. Chiều và tốc độ truyền của sóng là
- A từ phải sang trái, với tốc độ 1,2m/s
- B từ trái sang phải, với tốc độ 1,2m/s
- C từ phải sang trái, với tốc độ 0,6m/s
- D từ trái sang phải, với tốc độ 0,6m/s
Phương pháp giải:
Hệ thức độc lập \({{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}\)
Khoảng cách giữa hai điểm dao động cực tiểu là một nửa bước sóng
Tần số góc ω = 2πf
Bước sóng λ = v/f
Lời giải chi tiết:
Ta có: A = 4cm, x = \(2\sqrt{2}\) cm, v = \(20\pi \sqrt{2}\)
Áp dụng hệ thức độc lập: \({{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}\) => ω = 10π rad/s => f = 5Hz
Bước sóng \(\lambda =\frac{v}{f}\Rightarrow v=\lambda f\)
Vì OM = 9cm nên λ > 18cm => v > 0,9m/s
Vì M có xu hướng đi xuống nên nó nhận dao động từ bên phải truyền tới.
Chọn A