Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với giá trị nào của tham số \(m\) thì phương trình \(\left| {f\left( x \right)} \right| = m\) có năm nghiệm phân biệt thuộc đoạn \(\left[ {0;5} \right]\)?
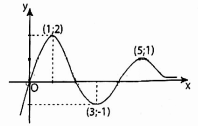
- A \(m \in \left( {0;1} \right)\)
- B \(m \in \left( {1; + \infty } \right)\)
- C \(m \in \left[ {0;1} \right]\)
- D \(m \in \left( {0;1} \right]\)
Phương pháp giải:
- Vẽ phác đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) từ đồ thị hàm số \(y = f\left( x \right)\) đã cho (lấy đối xứng phần dưới trục hoành qua trục hoành và giữ nguyên phần phía trên trục hoành).
- Sử dụng tương giao đồ thị suy ra tập giá trị của \(m\).
Lời giải chi tiết:
Từ đồ thị hàm số đã cho ta dựng được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như sau:
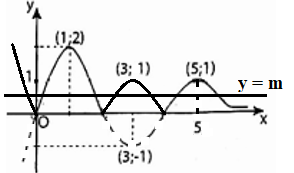
Quan sát đồ thị hàm số ta thấy, trên đoạn \(\left[ {0;5} \right]\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) tại đúng \(5\) điểm phân biệt nếu và chỉ nếu \(0 < m < 1\).
Chọn A.







