Câu hỏi
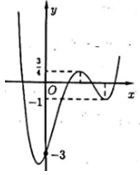
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ. Số giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {x + m} \right|} \right) = m\) có 4 nghiệm phân biệt là:
- A \(2\)
- B Vô số
- C \(1\)
- D \(0\)
Phương pháp giải:
Đồ thị hàm số \(f\left( {\left| {x + m} \right|} \right)\) được tạo thành bằng cách.
+) Từ đồ thị hàm số \(f\left( x \right)\) suy ra đồ thị hàm số \(f\left( {\left| x \right|} \right)\).
+) Từ đồ thị hàm số \(f\left( {\left| x \right|} \right)\) suy ra đồ thị hàm số \(f\left( {\left| {x + m} \right|} \right)\) bằng cách tịnh tiến đồ thị hàm số \(f\left( {\left| x \right|} \right)\) dọc theo trục \(Ox\) sang bên trái \(m\) đơn vị.
Lời giải chi tiết:
Đồ thị hàm số \(f\left( {\left| {x + m} \right|} \right)\) được tạo thành bằng cách.
+) Từ đồ thị hàm số \(f\left( x \right)\) suy ra đồ thị hàm số \(f\left( {\left| x \right|} \right)\) bằng cách giữ đồ thị hàm số \(f\left( x \right)\) bên phải trục hoành, xóa đi phần đồ thị hàm số bên trái trục hoành và lấy đối xứng đồ thị hàm số \(f\left( x \right)\) bên phải trục hoành qua trục hoành.
+) Từ đồ thị hàm số \(f\left( {\left| x \right|} \right)\) suy ra đồ thị hàm số \(f\left( {\left| {x + m} \right|} \right)\) bằng cách tịnh tiến đồ thị hàm số \(f\left( {\left| x \right|} \right)\) dọc theo trục \(Ox\) sang bên trái \(m\) đơn vị.
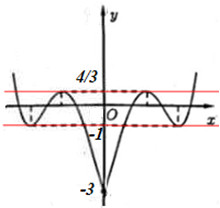
Từ đó ta có đồ thị hàm số \(f\left( {\left| x \right|} \right)\) như sau:
Quá trình tịnh tiến đồ thị hàm số \(f\left( {\left| x \right|} \right)\) dọc theo trục \(Ox\) sang bên trái \(m\) đơn vị không làm thay đổi số tương giao, do đó phương trình \(f\left( {\left| {x + m} \right|} \right) = m\) có 4 nghiệm phân biệt khi và chỉ khi \(m = - 1\) hoặc \(m = \dfrac{4}{3}\). Mà \(m \in \mathbb{Z} \Rightarrow m = - 1\).
Vậy có 1 giá trị \(m\) thỏa mãn yêu cầu bài toán.
Chọn C.