Phương pháp giải:

Cô lập \(m\) đưa bất phương trình về dạng \(m \ge f\left( x \right);\,\forall x \in \mathbb{R}\) suy ra \(m \ge \mathop {\max }\limits_\mathbb{R} f\left( x \right)\)

Ta tính \(f'\left( x \right)\) rồi lập BBT của \(f\left( x \right)\) và kết luận

Lời giải chi tiết:

Ta có \(m{x^4} - 4x + m \ge 0 \Leftrightarrow m\left( {{x^4} + 1} \right) \ge 4x \Leftrightarrow m \ge \dfrac{{4x}}{{{x^4} + 1}} = f\left( x \right)\,\,\,\left( {Do\,\,{x^4} + 1 > 0\,\,\forall x} \right)\) với \(\forall x \in \mathbb{R}\)

\( \Rightarrow m \ge \mathop {\max }\limits_\mathbb{R} f\left( x \right)\) 

Xét hàm \(f\left( x \right) = \dfrac{{4x}}{{{x^4} + 1}}\) trên \(\mathbb{R}\).

Ta có \(f'\left( x \right) = 4\dfrac{{{x^4} + 1 - x.4{x^3}}}{{{{\left( {{x^4} + 1} \right)}^2}}} = 4.\dfrac{{ - 3{x^4} + 1}}{{{{\left( {{x^4} + 1} \right)}^2}}} = 4.\dfrac{{\left( {1 - \sqrt 3 {x^2}} \right)\left( {1 + \sqrt 3 {x^2}} \right)}}{{{{\left( {{x^4} + 1} \right)}^2}}}\)

Từ đó \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{{\sqrt[4]{3}}}\\x =  - \dfrac{1}{{\sqrt[4]{3}}}\end{array} \right.\)

Ta có BBT :

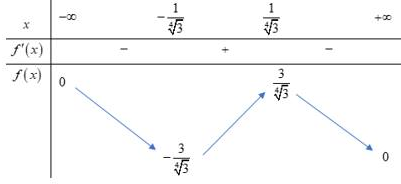
Từ BBT suy ra \(m \ge \dfrac{3}{{\sqrt[4]{3}}} \approx 2,27\)  mà \(m\) nguyên và \(m \in \left[ { - 50;50} \right] \Rightarrow m \in \left\{ {3;4;...;50} \right\}\)

Tổng \(S = 3 + 4 + ... + 50 = \dfrac{{\left( {3 + 50} \right).48}}{2} = 1272\)

Chọn A.