Câu hỏi
Biết rằng thiết diện qua trục của một hình nón là tam giác đều có diện tích bằng \({a^2}\sqrt 3 .\) Tính thể tích \(V\) của khối nón đã cho.
- A \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{2}\)
- B \(V = \dfrac{{\pi {a^3}\sqrt 6 }}{6}\)
- C \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{3}\)
- D \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{6}\)
Phương pháp giải:
Công thức tính thể tích của khối nón có bán kính đáy 
và chiều cao \(h:\;\;\;V = \dfrac{1}{3}\pi {R^2}h.\)
Lời giải chi tiết:
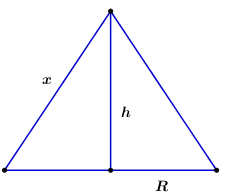
Gọi cạnh của tam giác đều qua trục là \(x\)
\( \Rightarrow S = \dfrac{{{x^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \Leftrightarrow {x^2} = 4{a^2} \Leftrightarrow x = 2a.\)
\( \Rightarrow \) Bán kính đáy của hình nón là: \(R = \dfrac{x}{2} = a,\) chiều cao của hình nón là: \(h = \dfrac{{x\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 .\)
\( \Rightarrow {V_{non}} = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a\sqrt 3 = \dfrac{{\pi {a^3}\sqrt 3 }}{3}.\)
Chọn C.
Câu hỏi trước
