Câu hỏi
Cho đường tròn \(\left( C \right):{x^2} + {y^2} - 8x + 6y + 21 = 0\) và đường thẳng \(d:x + y - 1 = 0\). Xác định tọa độ các đỉnh A của hình vuông ABCD ngoại tiếp \(\left( C \right)\) biết \(A \in d\).
- A \(A\left( {2; - 1} \right)\) hoặc \(A\left( {5; - 4} \right)\).
- B \(A\left( {2; - 1} \right)\) hoặc \(A\left( { - 6;7} \right)\).
- C \(A\left( { - 2;3} \right)\) hoặc \(A\left( {6; - 5} \right)\).
- D \(A\left( {2; - 1} \right)\) hoặc \(A\left( {6; - 5} \right)\).
Phương pháp giải:
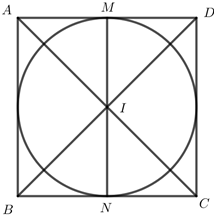
Xác định tâm I và bán kính của đường tròn \(\left( C \right)\), tính AI theo hình vẽ, gọi A theo 1 chữ tìm tọa độ của A
Lời giải chi tiết:
Đường tròn \(\left( C \right)\) có tâm \(I\left( {4; - 3} \right)\) bán kính \(R = \sqrt {16 + 9 - 21} = 2\)
\( \Rightarrow \left( C \right):\,\,\,{\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} = 4.\)
Do hình vuông ABCD ngoại tiếp \(\left( C \right)\)
\(\begin{array}{l} \Rightarrow MN = 2R = 4 = AB = AD\\ \Rightarrow AM = \frac{1}{2}AD = 2\\ \Rightarrow A{I^2} = {2^2} + {2^2} = 8\end{array}\)
Gọi \(A\left( {a;\,\,1 - a} \right) \in \left( d \right) \Rightarrow {\left( {4 - a} \right)^2} + {\left( {a - 4} \right)^2} = 8\)
\( \Leftrightarrow 2{\left( {a - 4} \right)^2} = 8 \Leftrightarrow \left[ \begin{array}{l}a - 4 = 2\\a - 4 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 6 \Rightarrow A\left( {6; - 5} \right)\\a = 2 \Rightarrow A\left( {2; - 1} \right)\end{array} \right.\)
Chọn D.