Câu hỏi
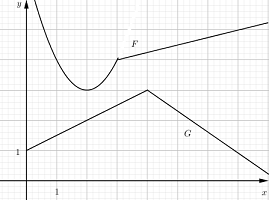
Cho \(y = F\left( x \right)\) và \(y = G\left( x \right)\) là những hàm số có đồ thị cho trong hình bên dưới, đặt \(P\left( x \right) = F\left( x \right)G\left( x \right).\) Tính \(P'\left( 2 \right).\)
- A \(\dfrac{5}{2}\)
- B \(4\)
- C \(\dfrac{3}{2}\)
- D
\(6\)
Phương pháp giải:
Sử dụng công thức tính đạo hàm của hàm số: \(\left[ {f\left( x \right).g\left( x \right)} \right]' = f'\left( x \right)g\left( x \right) + f\left( x \right).g'\left( x \right).\)
Lời giải chi tiết:
Xét khoảng \(\left( {0;\,3} \right)\) ta có: \(\left\{ \begin{array}{l}F\left( x \right) = {x^2} - 4x + 7\\G\left( x \right) = \dfrac{1}{2}x + 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}F'\left( x \right) = 2x - 4\\G'\left( x \right) = \dfrac{1}{2}\end{array} \right.\)
Ta có: \(P\left( x \right) = F\left( x \right).G\left( x \right)\)
\(\begin{array}{l} \Rightarrow P'\left( x \right) = F'\left( x \right).G\left( x \right) + F\left( x \right).G'\left( x \right)\\ \Rightarrow P'\left( 2 \right) = F'\left( 2 \right).G\left( 2 \right) + F\left( 2 \right).G'\left( 2 \right)\\ = \left( {2.2 - 4} \right).2 + 3.\dfrac{1}{2} = \dfrac{3}{2}.\end{array}\)
Chọn C.







