Câu hỏi
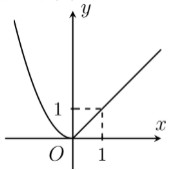
Cho đồ thị của hàm số \(y = f\left( x \right)\). Hãy chọn mệnh đề đúng.
- A
Hàm số \(y = f\left( x \right)\) có đạo hàm tại \(x = 0\) nhưng không liên tục tại \(x = 0\).
- B Hàm số \(y = f\left( x \right)\) liên tục tại \(x = 0\) nhưng không có đạo hàm tại \(x = 0\).
- C Hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm tại \(x = 0\).
- D Hàm số \(y = f\left( x \right)\) không liên tục và không có đạo hàm tại \(x = 0\).
Phương pháp giải:
+) Hàm số có đạo hàm tại \(x = {x_0}\) thì hàm số đó phải liên tục tại \(x = {x_0}\).
+) Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\) khi và chỉ khi hàm số xác định tại \(x = {x_0}\) và \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = f\left( {{x_0}} \right)\).
Lời giải chi tiết:
Dễ thấy hàm số liên tục tại \(x = 0\) vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) = 0\).
\( \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x} \Rightarrow \) Hàm số có đạo hàm tại \(x = 0\).
Chọn C.







