Câu hỏi
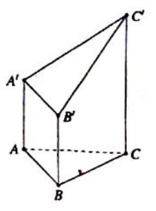
Cho hình đa diện như hình vẽ, trong đó các cạnh AA’, BB’, CC’ đều vuông góc với (ABC), tam giác ABC đều cạnh a và \(AA' = BB' = \dfrac{1}{2}CC' = a\). Tính theo a thể tích V của khối đa diện đó.
- A \(V = \dfrac{{{a^3}\sqrt 3 }}{6}\).
- B \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\).
- C \(V = \dfrac{{4{a^3}\sqrt 3 }}{3}\).
- D \(V = \dfrac{{3{a^3}\sqrt 3 }}{4}\).
Phương pháp giải:
Cắt khối đa diện đã cho làm hai khối: khối lăng trụ và khối tứ diện.
Lời giải chi tiết:
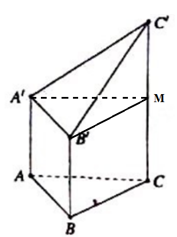
Gọi M là trung điểm của CC’.
Khi đó: khối đa diện đã cho được chia làm 2 phần: Khối lăng trụ tam giác đều \(A'B'M.ABC\) và khối tứ diện \(A'B'C'M\).
Thể tích khối lăng trụ tam giác đều \(A'B'M.ABC\) là:
\({V_{A'B'M.ABC}} = {S_{\Delta ABC}}.AA' = \dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{4}\)
\(\begin{array}{l}C'M = \dfrac{1}{2}CC' = a,\,\,C'M \bot \left( {A'B'M} \right)\\ \Rightarrow {V_{A'B'C'M}} = \dfrac{1}{3}.{S_{\Delta A'B'M}}.C'M = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{{12}}\end{array}\)
\( \Rightarrow \)Thể tích cần tìm là: \(V = \dfrac{{{a^3}\sqrt 3 }}{4} + \dfrac{{{a^3}\sqrt 3 }}{{12}} = \dfrac{{{a^3}\sqrt 3 }}{3}\).
Chọn: B