Câu hỏi
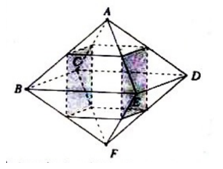
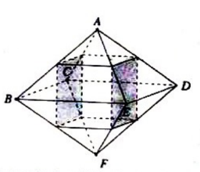
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ)
- A \(V = {a^3}\sqrt 2 \).
- B \(V = \dfrac{{{a^3}\sqrt 2 }}{4}\).
- C \(V = \dfrac{{{a^3}\sqrt 2 }}{2}\).
- D \(V = \dfrac{{{a^3}\sqrt 2 }}{8}\).
Phương pháp giải:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF (như hình vẽ) là hình hộp chữ nhật.
Lời giải chi tiết:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF là hình hộp chữ nhật có đáy là hình vuông cạnh \(\dfrac{a}{2}\); chiều cao \(h = \dfrac{1}{2}AF = \dfrac{1}{2}.a\sqrt 2 = \dfrac{{a\sqrt 2 }}{2}\) (do ABFD là hình vuông cạnh a).
Thể tích khối đa diện đó là: \(V = {\left( {\dfrac{a}{2}} \right)^2}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{8}\).
Chọn: D