Câu hỏi
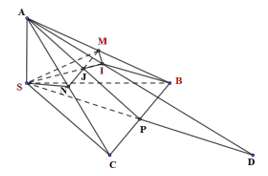
Cho hình chóp S.ABC có mỗi mặt bên là một tam giác vuông và \(SA = SB = SC = a\). Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC; D là điểm đối xứng của S qua P. I là giao điểm của đường thẳng AD với mặt phẳng (SMN). Tính theo a thể tích của khối tứ diện MBSI.
- A \(\dfrac{{{a^3}}}{{12}}\).
- B \(\dfrac{{{a^3}}}{{36}}\).
- C \(\dfrac{{{a^3}}}{6}\).
- D \(\dfrac{{\sqrt 2 {a^3}}}{{12}}\).
Phương pháp giải:
Sử dụng tỉ số diện tích, tỉ số thể tích để tính thể tích khối tứ diện MBSI thông qua thể tích khối tứ diện vuông SABC.
Lời giải chi tiết:
Do \(SA = SB = SC = a\) nên các tam giác \(SAB,\,\,SBC,\,\,SCA\) vuông tại S.
\( \Rightarrow SA,SB,SC\) đôi một vuông góc.
Thể tích khối tứ diện vuông S.ABC là: \(V = \dfrac{1}{6}.SA.SB.SC = \dfrac{{{a^3}}}{6}\)
Gọi J là giao điểm của MN và AP, I là giao điểm của SJ và AD. Khi đó, \(I = AD \cap \left( {SMN} \right)\) (do \(SI \subset \left( {SMN} \right)\))
\(\Delta ASD\) có: P là trung điểm của SD, J là trung điểm của AP.
Xét tam giác vuông SBC có \(SP = \dfrac{1}{2}BC = \dfrac{{a\sqrt 2 }}{2} \Rightarrow AP = \sqrt {S{A^2} + S{P^2}} = \dfrac{{a\sqrt 6 }}{2}\).
\( \Rightarrow SJ = \dfrac{1}{2}AP = \dfrac{{a\sqrt 6 }}{4}\).
Ta có: \(SD = 2SP = a\sqrt 2 \Rightarrow AD = a\sqrt 3 \Rightarrow \cos \angle SDA = \dfrac{{SD}}{{AD}} = \dfrac{{\sqrt 6 }}{3}\).
Áp dụng định lí Menelaus trong tam giác APD ta có:
\(\dfrac{{JA}}{{JP}}.\dfrac{{SP}}{{SD}}.\dfrac{{ID}}{{IA}} = 1 \Leftrightarrow 1.\dfrac{1}{2}.\dfrac{{ID}}{{IA}} = 1 \Leftrightarrow \dfrac{{ID}}{{IA}} = 2 \Leftrightarrow ID = \dfrac{2}{3}AD = \dfrac{{2a\sqrt 3 }}{3}\)
Áp dụng định lí Cosin trong tam giác \(SID\) ta có:
\(\begin{array}{l}S{I^2} = S{D^2} + D{I^2} - 2SD.DI.\cos \angle SDA\\\,\,\,\,\,\,\,\,\, = 2{a^2} + \dfrac{4}{3}{a^2} - 2.a\sqrt 2 .\dfrac{{2a\sqrt 3 }}{3}.\dfrac{{\sqrt 6 }}{3} = \dfrac{{2{a^2}}}{3}\\ \Rightarrow SI = \dfrac{{a\sqrt 6 }}{3} \Rightarrow \dfrac{{SJ}}{{SI}} = \dfrac{3}{4}\end{array}\)
Dễ dàng chứng minh được: \(SJ = \dfrac{3}{4}SI\)\( \Rightarrow {S_{\Delta SJB}} = \dfrac{3}{4}{S_{\Delta SIB}}\)\( \Rightarrow {V_{M.SJB}} = \dfrac{3}{4}{V_{M.SIB}}\) hay \( \Rightarrow {V_{M.SIB}} = \dfrac{4}{3}{V_{M.SJB}}\)
Lại có: \({S_{\Delta MJB}} = \dfrac{1}{2}{S_{\Delta AJB}} = \dfrac{1}{2}.\dfrac{1}{2}{S_{\Delta APB}} = \dfrac{1}{8}{S_{\Delta ABC}}\)
\( \Rightarrow {V_{M.SJB}} = \dfrac{1}{8}{V_{S.ABC}}\)\( \Rightarrow {V_{M.SIB}} = \dfrac{4}{3}.\dfrac{1}{8}{V_{S.ABC}} = \dfrac{1}{6}{V_{S.ABC}} = \dfrac{1}{6}.\dfrac{1}{6}{a^3} = \dfrac{1}{{36}}{a^3}\).
Chọn: B