Phương pháp giải:

- Xác định thiết diện của tứ diện khi cắt bởi \(\left( {MNP} \right)\).

- Phân chia các khối đa diện thành cách khối chóp tam giác có thể tính được tỉ số thê tích.

- Tính các tỉ số đoạn thẳng, suy ra tỉ số thể tích các khối chóp tam giác theo định lý tỉ số thể tích.

Lời giải chi tiết:

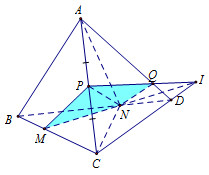
Gọi \({V_{ABCD}} = V\), \(I = MN \cap CD\), \(Q = IP \cap AD\) ta có \(Q = AD \cap \left( {MNP} \right)\)

Thiết diện của tứ diện \(ABCD\) được cắt bởi mặt phẳng \(\left( {MNP} \right)\) là tứ giác \(MNQP\).

Áp dụng định lí Menelaus trong các tam giác \(BCD\) và \(ACD\) ta có:

\(\dfrac{{NB}}{{ND}}.\dfrac{{ID}}{{IC}}.\dfrac{{MC}}{{MB}} = 1\) \( \Rightarrow \dfrac{{ID}}{{IC}} = \dfrac{1}{4}\) và \(\dfrac{{ID}}{{IC}}.\dfrac{{PC}}{{PA}}.\dfrac{{QA}}{{QD}} = 1\) \( \Rightarrow \dfrac{{QA}}{{QD}} = 4\).

Áp dụng bài toán tỉ số thể tích của hai khối chóp tam giác, ta có:

\(\dfrac{{{V_{ANPQ}}}}{{{V_{ANCD}}}}\)\( = \dfrac{{AP}}{{AC}}.\dfrac{{AQ}}{{AD}}\)\( = \dfrac{2}{5}\)\( \Rightarrow {V_{ANPQ}} = \dfrac{2}{5}{V_{ANCD}} = \dfrac{2}{5}.\dfrac{{ND}}{{BD}}.{V_{ABCD}}\)\( = \dfrac{2}{5}.\dfrac{1}{3}V = \dfrac{2}{{15}}V\).

Suy ra \({V_{N.PQDC}} = \dfrac{1}{3}V - \dfrac{2}{{15}}V\)\( = \dfrac{1}{5}V\).

Và \(\dfrac{{{V_{CMNP}}}}{{{V_{CBNA}}}}\)\( = \dfrac{{CM}}{{CB}}.\dfrac{{CP}}{{CA}}\)\( = \dfrac{1}{3}\)\( \Rightarrow {V_{CMNP}} = \dfrac{1}{3}{V_{CBNA}}\)\( = \dfrac{1}{3}.\dfrac{2}{3}{V_{ABCD}} = \dfrac{2}{9}V\).

Suy ra \({V_2} = {V_{N.PQDC}} + {V_{CMNP}} = \dfrac{{19}}{{45}}V\). Do đó \({V_1} = V - {V_2}\)\( = \dfrac{{26}}{{45}}V\). Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{26}}{{19}}\).

Chọn B.