Phương pháp giải:

+ Xác định góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right):\) \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \bot d;\,a \in \left( P \right)\\b \bot d;b \in \left( Q \right)\end{array} \right. \Rightarrow \) góc giữa \(\left( P \right)\) và \(\left( Q \right)\) là góc giữa hai đường thẳng \(a;b.\)

+ Tính toán dựa vào định lý Pytago và hệ thức lượng trong tam giác vuông

+ Thể tích khối chóp có chiều cao \(h\) và diện tích đáy \(S\) là \(V = \dfrac{1}{3}h.S\)

Lời giải chi tiết:

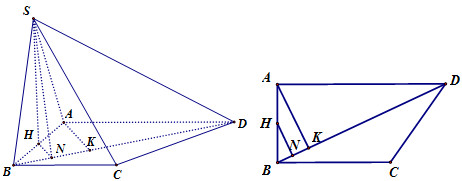
Gọi \(H\) là trung điểm của \(AB,\) kẻ \(AK \bot BD\) tại \(K\) và \(HN \bot BD\) tại \(N \Rightarrow AK//HN \Rightarrow HN = \dfrac{1}{2}AK\)  (đường trung bình tam giác \(ABK\))

Khi đó ta có \(BD \bot HN;\,BD \bot SH\left( {SH \bot \left( {ABCD} \right)} \right) \Rightarrow BD \bot \left( {SHN} \right) \Rightarrow BD \bot SN\)

Suy ra \(\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {ABCD} \right) = BD\\HN \bot BD;\,HN \subset \left( {ABCD} \right)\\SN \bot BD;SN \subset \left( {SBD} \right)\end{array} \right. \Rightarrow \) góc giữa \(\left( {SBD} \right)\) và \(\left( {ABCD} \right)\) là góc \(SNH \Rightarrow \widehat {SNH} = 60^\circ \)

Xét tam giác vuông \(ABD\) có \(AD = \sqrt {B{D^2} - A{B^2}}  = \sqrt {10 - 1}  = 3\) và

\(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}} = \dfrac{1}{1} + \dfrac{1}{9} = \dfrac{{10}}{9} \Rightarrow AK = \dfrac{3}{{\sqrt {10} }}\) nên \(HN = \dfrac{1}{2}AK = \dfrac{3}{{2\sqrt {10} }}\)

Xét tam giác \(SHN\) vuông tại \(H\) có \(SH = HN.\tan \widehat {SNH} = \dfrac{3}{{2\sqrt {10} }}.\tan 60^\circ  = \dfrac{{3\sqrt 3 }}{{2\sqrt {10} }}\)

Diện tích đáy \(BCD\) là  \({S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{\left( {BC + AD} \right).AB}}{2} - \dfrac{{AB.AD}}{2} = \dfrac{5}{2} - \dfrac{3}{2} = 1\)

Thể tích khối chóp \(S.BCD\) là \({V_{S.BCD}} = \dfrac{1}{3}SH.{S_{BCD}} = \dfrac{1}{3}.\dfrac{{3\sqrt 3 }}{{2\sqrt {10} }}.1 = \dfrac{{\sqrt {30} }}{{20}}\) .

Chọn C.