Phương pháp giải:

Khi quay tam giác \(AA'C\) quanh trục \(AA'\) ta được hình nón có bán kính đáy \(R = AC,\,\) đường sinh \(l = A'C'\) và chiều cao \(h = AA'.\)

Công thức tính diện tích toàn phần hình nón có bán kính đáy \(R,\;\) chiều cao \(h\) và đường sinh \(l:\;\;{S_{tp}} = \pi Rl + \pi {R^2}.\)

Lời giải chi tiết:

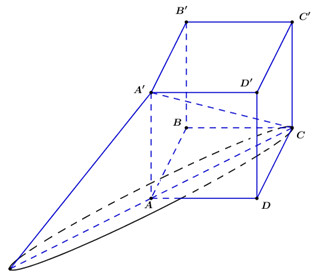
Khi quay tam giác \(AA'C\) quanh trục \(AA'\) ta được hình nón có bán kính đáy \(R = AC,\,\) đường sinh \(l = A'C'\) và chiều cao \(h = AA'.\)

Ta có: \(AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2 .\)

\(\begin{array}{l}A'C = \sqrt {A{C^2} + AA{'^2}}  = \sqrt {2{a^2} + {a^2}}  = a\sqrt 3 \\ \Rightarrow {S_{tp}} = \pi Rl + \pi {R^2} = \pi .AC.A'C + \pi .A{C^2}\\ = \pi \left( {a\sqrt 2 .a\sqrt 3  + 2{a^2}} \right) = \pi \left( {\sqrt 6  + 2} \right){a^2}.\end{array}\)

Chọn A.