Câu hỏi
Cho hình chóp tứ giác \(SABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\) mặt bên \(SAB\) là một tam giác đều và nằm trong một mặt phẳng vuông góc với đáy \(\left( {ABCD} \right).\) Tính thể tích khối chóp \(SABCD.\)
- A \(\dfrac{{{a^3}}}{6}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
- D \(\dfrac{{{a^3}}}{2}\)
Phương pháp giải:
Công thức tính thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \frac{1}{3}Sh.\)
Lời giải chi tiết:
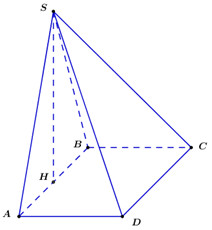
Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot \left( {ABCD} \right).\)
\(\begin{array}{l} \Rightarrow SH = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{2}.\\ \Rightarrow {V_{SABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 3 }}{6}.\end{array}\)
Chọn C.
Câu hỏi trước
