Câu hỏi
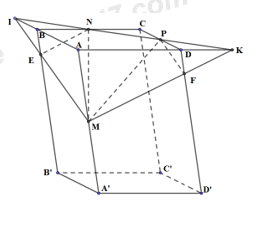
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P lần lượt là trung điểm của AA’, BC, CMặt phẳng (MNP) chia khối hộp thành hai phần có thể tích là \({V_1},{V_2}\). Gọi \({V_1}\) là thể tích phần chứa điểm Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng
- A \(\dfrac{{119}}{{25}}\).
- B \(\dfrac{3}{4}\).
- C \(\dfrac{{113}}{{24}}\).
- D \(\dfrac{{119}}{{425}}\).
Phương pháp giải:
Thể tích khối chóp : \(V = \dfrac{1}{3}Sh\)
Thể tích khối lăng trụ: \(V = Sh\).
Lời giải chi tiết:
Trong (ABCD), gọi \(I = NP \cap AB,\,\,K = NP \cap AD\)
Trong (ABB’A’), gọi \(E = IM \cap BB'\)
Trong (ADD’A’), gọi \(F = KM \cap DD'\)
Thiết diện của hình hộp cắt bởi (MNP) là ngũ giác MENPF.
Ta có: \(\Delta INB = \Delta PNC \Rightarrow IN = NP\), tương tự:
\(KP = NP \Rightarrow IN = KP = NP\)
\( \Rightarrow \dfrac{{IN}}{{IK}} = \dfrac{1}{3} \Rightarrow \dfrac{{IN}}{{IK}} = \dfrac{{BE}}{{AM}} = \dfrac{{IB}}{{IA}} = \dfrac{1}{3}\)
\( \Rightarrow \dfrac{{{V_{E.IBN}}}}{{{V_{M.IAK}}}} = \dfrac{1}{{27}}\)
Tương tự: \(\dfrac{{{V_{F.DPK}}}}{{{V_{M.IAK}}}} = \dfrac{1}{{27}}\)\( \Rightarrow \dfrac{{{V_2}}}{{{V_{M.IAK}}}} = 1 - \dfrac{1}{{27}} - \dfrac{1}{{27}} = \dfrac{{25}}{{27}} \Rightarrow {V_2} = \dfrac{{25}}{{27}}{V_{M.IAK}}\)
Ta có: \(\Delta IAK\) đồng dạng \(\Delta NCP\) với tỉ số đồng dạng là \(3 \Rightarrow {S_{\Delta AIK}} = 9.{S_{\Delta NCP}}\).
Mà \({S_{\Delta NCP}} = \dfrac{1}{4}.\dfrac{1}{2}.{S_{ABCD}} = \dfrac{1}{8}{S_{ABCD}}\)
\( \Rightarrow {S_{\Delta AIK}} = \dfrac{9}{8}{S_{ABCD}}\)
Khi đó:
\({V_{M.IAK}} = \dfrac{1}{2}.\dfrac{9}{8}.{V_{A'.ABCD}} = \dfrac{1}{2}.\dfrac{9}{8}.\dfrac{1}{3}.{V_{ABCD.A'B'C'D'}} = \dfrac{3}{{16}}{V_{ABCD.A'B'C'D'}}\)\( \Rightarrow {V_2} = \dfrac{{25}}{{27}}{V_{M.IAK}} = \dfrac{{25}}{{27}}.\dfrac{3}{{16}}{V_{ABCD.A'B'C'D'}} = \dfrac{{25}}{{144}}{V_{ABCD.A'B'C'D'}}\)
\( \Rightarrow {V_1} = \dfrac{{119}}{{144}}{V_{ABCD.A'B'C'D'}}\)\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \)\(\dfrac{{119}}{{25}}\).
Chọn: A