Câu hỏi
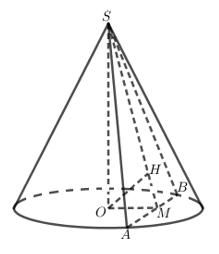
Cho hình nón đỉnh \(S\) có bán kính đáy bằng \(a\sqrt 2 .\) Mặt phẳng \(\left( P \right)\) qua \(S\) cắt đường tròn đáy tại \(A,B\) sao cho \(AB = 2a.\) Biết rằng khoảng cách từ tâm đường tròn đáy đến mặt phẳng \(\left( P \right)\) là \(\dfrac{{4a\sqrt {17} }}{{17}}.\) Thể tích khối nón bằng
- A \(\dfrac{8}{3}\pi {a^3}.\)
- B \(2\pi {a^3}.\)
- C \(\dfrac{{10}}{3}\pi {a^3}.\)
- D \(4\pi {a^3}.\)
Phương pháp giải:
- Gọi \(M\) là trung điểm \(AB\), dựng đường cao kẻ từ \(O\) đến mặt phẳng \(\left( P \right)\).
- Tính thể tích khối nón theo công thức \(V = \dfrac{1}{3}\pi {R^2}h\).
Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(AB\), kẻ \(OH \bot SM\).
Khi đó \(OM \bot AB,SM \bot AB \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\).
Lại có \(OH \bot SM\) nên \(OH \bot \left( {SAB} \right) \Rightarrow d\left( {O,\left( P \right)} \right) = OH = \dfrac{{4a\sqrt {17} }}{{17}}.\)
Xét tam giác \(OAM\) vuông tại \(M\) có \(OA = a\sqrt 2 ,MA = \dfrac{{AB}}{2} = a \Rightarrow OM = \sqrt {O{A^2} - A{M^2}} = a\).
Xét tam giác \(SOM\) vuông tại \(O\) có \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}} \Rightarrow \dfrac{{17}}{{16{a^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{{a^2}}} \Rightarrow SO = 4a\).
Vậy thể tích khối nón \(V = \dfrac{1}{3}\pi .O{A^2}.SO = \dfrac{1}{3}\pi .2{a^2}.4a = \dfrac{{8\pi {a^3}}}{3}\).
Chọn A.